92.(08四川资阳24题)24．(本小题满分12分)

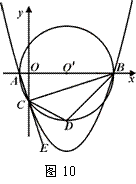如图10，已知点A的坐标是(－1，0)，点B的坐标是(9，0)，以AB为直径作⊙O′，交y轴的负半轴于点C，连接AC、BC，过A、B、C三点作抛物线．

(1)求抛物线的解析式；

(2)点E是AC延长线上一点，∠BCE的平分线CD交⊙O′于点D，连结BD，求直线BD的解析式；

(3)在(2)的条件下，抛物线上是否存在点P，使得∠PDB＝∠CBD?如果存在，请求出点P的坐标；如果不存在，请说明理由．

(08四川资阳24题解答)(1) ∵以AB为直径作⊙O′，交y轴的负半轴于点C，

∴∠OCA+∠OCB=90°，

又∵∠OCB+∠OBC=90°，

∴∠OCA=∠OBC，

又∵∠AOC= ∠COB=90°，

∴ΔAOC∽ ΔCOB，························································································· 1分

∴．

又∵A(–1，0)，B(9，0)，

∴，解得OC=3(负值舍去)．

∴C(0，–3)，

······················································································································ 3分

设抛物线解析式为y=a(x+1)(x–9)，

∴–3=a(0+1)(0–9)，解得a=，

∴二次函数的解析式为y=(x+1)(x–9)，即y=x²–x–3．···························· 4分

(2) ∵AB为O′的直径，且A(–1，0)，B(9，0)，

∴OO′=4，O′(4，0)，····················································································· 5分

∵点E是AC延长线上一点，∠BCE的平分线CD交⊙O′于点D，

∴∠BCD=∠BCE=×90°=45°，

连结O′D交BC于点M，则∠BO′D=2∠BCD=2×45°=90°，OO′=4，O′D=AB=5．

∴D(4，–5)．································································································· 6分

∴设直线BD的解析式为y=kx+b(k≠0)

∴··························································· 7分

解得

∴直线BD的解析式为y=x–9.····································· 8分

(3) 假设在抛物线上存在点P，使得∠PDB=∠CBD，

解法一：设射线DP交⊙O′于点Q，则．

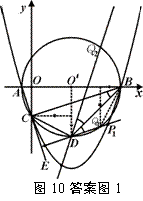
分两种情况(如答案图1所示)：

①∵O′(4，0)，D(4，–5)，B(9，0)，C(0，–3)．

∴把点C、D绕点O′逆时针旋转90°，使点D与点B重合，则点C与点Q₁重合，

因此，点Q₁(7，–4)符合，

∵D(4，–5)，Q₁(7，–4)，

∴用待定系数法可求出直线DQ₁解析式为y=x–．··································· 9分

解方程组得

∴点P₁坐标为(，)，[坐标为(，)不符合题意，舍去]．

······················································································································ 10分

②∵Q₁(7，–4)，

∴点Q₁关于x轴对称的点的坐标为Q₂(7，4)也符合．

∵D(4，–5)，Q₂(7，4)．

∴用待定系数法可求出直线DQ₂解析式为y=3x–17．······································ 11分

解方程组得

∴点P₂坐标为(14，25)，[坐标为(3，–8)不符合题意，舍去]．

······················································································································ 12分

∴符合条件的点P有两个：P₁(，)，P₂(14，25)．

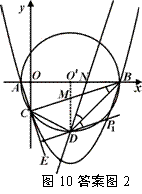解法二：分两种情况(如答案图2所示)：

①当DP₁∥CB时，能使∠PDB=∠CBD．

∵B(9，0)，C(0，–3)．

∴用待定系数法可求出直线BC解析式为y=x–3．

又∵DP₁∥CB，∴设直线DP₁的解析式为y=x+n．

把D(4，–5)代入可求n= –，

∴直线DP₁解析式为y=x–．························· 9分

解方程组得

∴点P₁坐标为(，)，[坐标为(，)不符合题意，舍去]．

······················································································································ 10分

②在线段O′B上取一点N，使BN=DM时，得ΔNBD≌ΔMDB(SAS)，∴∠NDB=∠CBD．

由①知，直线BC解析式为y=x–3．

取x=4，得y= –，∴M(4，–)，∴O′N=O′M=，∴N(，0)，

又∵D(4，–5)，

∴直线DN解析式为y=3x–17．······································································ 11分

解方程组得

∴点P₂坐标为(14，25)，[坐标为(3，–8)不符合题意，舍去]．

······················································································································ 12分

∴符合条件的点P有两个：P₁(，)，P₂(14，25)．

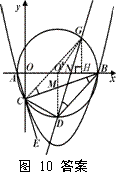
解法三：分两种情况(如答案图3所示)：

①求点P₁坐标同解法二．··············································································· 10分

②过C点作BD的平行线,交圆O′于G,

此时，∠GDB=∠GCB=∠CBD．

由(2)题知直线BD的解析式为y=x–9,

又∵ C(0，–3)

∴可求得CG的解析式为y=x–3,

设G(m,m–3)，作GH⊥x轴交与x轴与H，

连结O′G,在Rt△O′GH中，利用勾股定理可得，m=7，

由D(4，–5)与G(7，4)可得，

DG的解析式为，··········································································· 11分

解方程组得

∴点P₂坐标为(14，25)，[坐标为(3，–8)不符合题意，舍去]．························ 12分

∴符合条件的点P有两个：P₁(，)，P₂(14，25)．

说明：本题解法较多，如有不同的正确解法，请按此步骤给分.

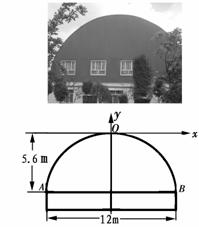
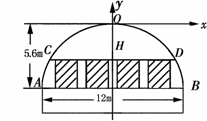
91.(08新疆自治区24题)(10分)某工厂要赶制一批抗震救灾用的大型活动板房．如图，板房一面的形状是由矩形和抛物线的一部分组成，矩形长为12m，抛物线拱高为5.6m．

(1)在如图所示的平面直角坐标系中，求抛物线的表达式．

(2)现需在抛物线AOB的区域内安装几扇窗户，窗户的底边在AB上，每扇窗户宽1.5m，高1.6m，相邻窗户之间的间距均为0.8m，左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m．请计算最多可安装几扇这样的窗户？

(08新疆自治区24题解析)24．(10分)解：(1)设抛物线的表达式为 1分

点在抛物线的图象上．

∴

······························································ 3分

∴抛物线的表达式为············································································· 4分

(2)设窗户上边所在直线交抛物线于C、D两点，D点坐标为(k，t)

已知窗户高1.6m，∴··························································· 5分

(舍去)············································································ 6分

∴(m)·············································································· 7分

又设最多可安装n扇窗户

∴····················································································· 9分

．

答：最多可安装4扇窗户．···················································································· 10分

(本题不要求学生画出4个表示窗户的小矩形)

24．解：(1)解法1：根据题意可得：A(-1,0)，B(3,0)；

则设抛物线的解析式为(a≠0)

又点D(0，-3)在抛物线上，∴a(0+1)(0-3)=-3，解之得：a=1

　∴y=x²-2x-3····································································································· 3分

自变量范围：-1≤x≤3···················································································· 4分

　　　　　 解法2：设抛物线的解析式为(a≠0)

　　　　　　 根据题意可知，A(-1,0)，B(3,0)，D(0，-3)三点都在抛物线上

∴，解之得：

∴y=x²-2x-3····································································································· 3分

自变量范围：-1≤x≤3····························································· 4分

　　　　　 (2)设经过点C“蛋圆”的切线CE交x轴于点E，连结CM，

　　　　　　 在Rt△MOC中，∵OM=1，CM=2，∴∠CMO=60°,OC=

　　　　　　 在Rt△MCE中，∵OC=2，∠CMO=60°，∴ME=4

　∴点C、E的坐标分别为(0，)，(-3,0) ·················································· 6分

∴切线CE的解析式为··························································· 8分

　(3)设过点D(0，-3)，“蛋圆”切线的解析式为：y=kx-3(k≠0) ························· 9分

　　　　　　　 由题意可知方程组只有一组解

　 即有两个相等实根，∴k=-2············································· 11分

　 ∴过点D“蛋圆”切线的解析式y=-2x-3····················································· 12分

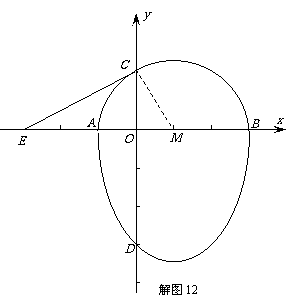
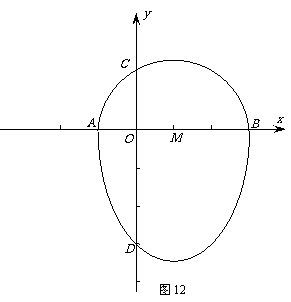
24.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线.

如图12，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为(0，-3)，AB为半圆的直径，半圆圆心M的坐标为(1,0)，半圆半径为2.

(1)　 请你求出“蛋圆”抛物线部分的解析式，并写出自变量的取值范围；

(2)你能求出经过点C的“蛋圆”切线的解析式吗？试试看；

(3)开动脑筋想一想，相信你能求出经过点D的“蛋圆”切线的解析式.

(08湖南益阳24题解析)七、(本题12分)

12.(08湖南长沙)26.如图，六边形ABCDEF内接于半径为r(常数)的⊙O，其中AD为直径，且AB=CD=DE=FA.

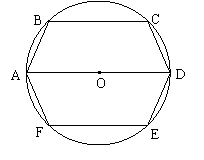(1)当∠BAD=75°时，求的长；

(2)求证：BC∥AD∥FE；

(3)设AB=，求六边形ABCDEF的周长L关于的函数关系式，并指出为何值时，L取得最大值.

(08湖南长沙26题解析)26．(1)连结OB、OC，由∠BAD=75°，OA=OB知∠AOB=30°，······ (1分)

∵AB=CD，∴∠COD=∠AOB=30°，∴∠BOC=120°，···································· (2分)

故的长为．··························································································· (3分)

(2)连结BD，∵AB=CD，∴∠ADB=∠CBD，∴BC∥AD，································· (5分)

同理EF∥AD，从而BC∥AD∥FE．································································· (6分)

(3)过点B作BM⊥AD于M，由(2)知四边形ABCD为等腰梯形，

从而BC=AD-2AM=2r-2AM．············································································ (7分)

∵AD为直径，∴∠ABD=90°，易得△BAM∽△DAB

∴AM==，∴BC=2r-，同理EF=2r-············································ (8分)

∴L=4x+2(2r-)==，其中0＜x＜ ·········· (9分)

∴当x=r时，L取得最大值6r．······································································ (10分)

13(08湖南益阳)七、(本题12分)

11.(08湖北咸宁)24．(本题(1)-(3)小题满分12分，(4)小题为附加题另外附加2分)

如图①，正方形 ABCD中，点A、B的坐标分别为(0，10)，(8，4)，点C在第一象限．动点P在正方形 ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴上运动，当P点到D点时，两点同时停止运动，设运动的时间为t秒．

(1)　 当P点在边AB上运动时，点Q的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；

(2) 求正方形边长及顶点C的坐标；

(3) 在(1)中当t为何值时，△OPQ的面积最大，并求此时P点的坐标．

(1)　 附加题：(如果有时间，还可以继续

解答下面问题，祝你成功！)

如果点P、Q保持原速度速度不

变，当点P沿A→B→C→D匀

速运动时，OP与PQ能否相等，

若能，写出所有符合条件的t的

值；若不能，请说明理由．

(08湖北咸宁24题解析)24．解：(1)(1,0)　 -----------------------------1分

　　　　　　 点P运动速度每秒钟1个单位长度．-------------------------------3分

　　　　 (2) 过点作BF⊥y轴于点，⊥轴于点，则＝8，.

　　　　　　 ∴.

　　　　　　 在Rt△AFB中，.----------------------------5分

　　　　　 过点作⊥轴于点,与的延长线交于点.

∵ ∴△ABF≌△BCH.

　∴.

∴.

∴所求C点的坐标为(14，12).------------7分

　　　　 (3) 过点P作PM⊥y轴于点M，PN⊥轴于点N，

则△APM∽△ABF.

　　　　　 ∴.　 .

　∴.　 ∴.

设△OPQ的面积为(平方单位)

∴(0≤≤10)　 ------------------10分

　　　 说明:未注明自变量的取值范围不扣分.

　∵<0　 ∴当时, △OPQ的面积最大.------------11分

　　　　 此时P的坐标为(，) .　 ---------------------------------12分

　　 (4)　 当 或时,　 OP与PQ相等.---------------------------14分

　　　　 对一个加1分,不需写求解过程.

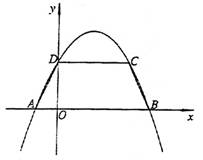
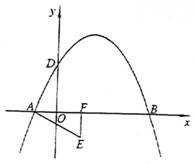
10.(08湖北武汉)(本题答案暂缺)25.(本题 12分)如图 1，抛物线y=ax2-3ax+b经过A(-1,0)，C(3,2)两点，与y轴交于点D，与x轴交于另一点B.(1)求此抛物线的解析式；(2)若直线y=kx-1(k≠0)将 四 边 形ABCD面积二等分，求k的值；(3)如图2，过点 E(1，-1)作EF⊥x轴于点F，将△AEF绕平面内某点旋转 180°后得△MNQ(点M，N，Q分别与 点 A，E，F对应)，使点M，N在抛物线上，求点M，N的坐标.

(08湖北武汉25题解析)25.⑴；⑵；⑶M(3，2)，N(1，3)

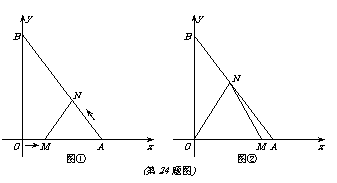
9.(08湖北天门)(本题答案暂缺)24．(本小题满分12分)如图①，在平面直角坐标系中，A点坐标为(3，0)，B点坐标为(0，4)．动点M从点O出发，沿OA方向以每秒1个单位长度的速度向终点A运动；同时，动点N从点A出发沿AB方向以每秒个单位长度的速度向终点B运动．设运动了x秒．

(1)点N的坐标为(________________，________________)；(用含x的代数式表示)

(2)当x为何值时，△AMN为等腰三角形？

(3)如图②，连结ON得△OMN，△OMN可能为正三角形吗？若不能，点M的运动速度不变，试改变点N的运动速度，使△OMN为正三角形，并求出点N的运动速度和此时x的值．

8.(08湖北荆州25题解析)(本题答案暂缺)25．(本题12分)如图，等腰直角三角形纸片ABC中，AC＝BC＝4，∠ACB＝90º，直角边AC在x轴上，B点在第二象限，A(1，0)，AB交y轴于E，将纸片过E点折叠使BE与EA所在直线重合，得到折痕EF(F在x轴上)，再展开还原沿EF剪开得到四边形BCFE，然后把四边形BCFE从E点开始沿射线EA平移，至B点到达A点停止.设平移时间为t(s)，移动速度为每秒1个单位长度，平移中四边形BCFE与△AEF重叠的面积为S.

　 (1)求折痕EF的长；

　 (2)是否存在某一时刻t使平移中直角顶点C经过抛物线的顶点？若存在，求出t值；若不存在，请说明理由；

　 (3)直接写出S与t的函数关系式及自变量t的取值范围.

7.(08湖北荆门)28．(本小题满分12分)

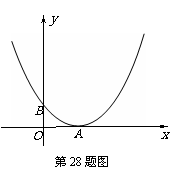
已知抛物线y=ax²+bx+c的顶点A在x轴上，与y轴的交点为B(0，1)，且b=－4ac．

　(1) 求抛物线的解析式；

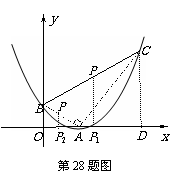
(2) 在抛物线上是否存在一点C，使以BC为直径的圆经过抛物线的顶点A？若不存在说明理由；若存在，求出点C的坐标，并求出此时圆的圆心点P的坐标；

(3) 根据(2)小题的结论，你发现B、P、C三点的横坐标之间、纵坐标之间分别有何关系?

(08湖北荆门28题解析)28．解：(1)由抛物线过B(0,1) 得c=1．

　　　　 又b=-4ac,　 顶点A(-,0),

　　　　 ∴-==2c=2．∴A(2,0)．　　　 ………………………………………2分

　　　　 将A点坐标代入抛物线解析式，得4a+2b+1=0 ，　　　

　∴ 　解得a =,b =-1.

　　　　 故抛物线的解析式为y=x²-x+1．　　　 ………………………………………4分

　　　 　另解: 由抛物线过B(0,1) 得c=1．又b²-4ac=0,　 b=-4ac，∴b=-1．　 ………2分

　　　　 ∴a=,故y=x-x+1．　　　　　 　……………………………………………4分

　 (2)假设符合题意的点C存在，其坐标为C(x，y),　 　　　　　　

　　　　 作CD⊥x轴于D ,连接AB、AC．

　　∵A在以BC为直径的圆上,∴∠BAC=90°．

　　　　 ∴ △AOB∽△CDA．

　　 　 ∴OB·CD=OA·AD．

　　　 　即1·y=2(x-2)， ∴y=2x-4． 　 ……………………6分

　　　　 由　　　 解得x₁=10,x₂=2．

∴符合题意的点C存在，且坐标为 (10,16)，或(2,0)．　 ………………………8分

　　　 ∵P为圆心，∴P为BC中点．

　　 　 当点C坐标为 (10,16)时，取OD中点P₁ ，连PP₁ ,　则PP₁为梯形OBCD中位线．

∴PP₁=(OB+CD)=．∵D (10,0),　∴P₁ (5,0),　∴P (5, )．　

　　　　 当点C坐标为 (2,0)时, 取OA中点P₂ ，连PP₂ ,　则PP₂为△OAB的中位线．

∴PP₂=OB=．∵A (2,0),　∴P₂(1,0), ∴P (1,)．　

故点P坐标为(5, ),或(1,)．　　……………………………………10分

(3)设B、P、C三点的坐标为B(x₁,y₁),　P(x₂,y₂),　C(x₃,y₃)，由(2)可知：

　　　　　　　　 ………………………………………12分