
2.命题作文:圆梦
以“圆梦”为题写一篇不少于800字的文章,自定立意,自选文体。
写作导引:
这是一道命题作文,构思时必须明白,由梦的本义延伸到希望、目标等。若没有吃好之梦,人类还在茹毛饮血;没有穿好之梦,人类现在还围着树叶;没有速度之梦,便不会有马车、汽车、火车等问世;没有飞翔之梦,便不会有飞机、飞船遨游天空;没有求知之梦,便没有今天灿烂的文化传承……由此可见,这里的梦应该是美梦,而非噩梦。
圆梦也有着广阔的背景:人类早期的许多“梦”,如今已成为现实。自改革开放以来,我们也圆了许多前辈先贤的梦,如三峡大坝全线建成,青藏铁路建成通车,“嫦娥一号”奔月成功。为此既可以抒写个人的奋斗历程,又可以赞美科技的力量、祖国的成就等;既可以围绕如何圆梦来写,又可以通过叙事表达自己圆梦的过程或圆梦时的感慨。既可以写自己克服重重困难,通过自己的努力获得了成功,又可以歌颂只为百姓梦圆抛却一生名利的奋斗者。更可以变换主体视角,由小草的圆梦表现当今环境污染严重这一普遍现实。但写作时必须明白以下几点:1.圆梦的过程是个持久的过程,它必须被付诸行动。2.梦是心灵的思想,是我们的真情,我们必须有梦,这样才能圆梦。3.一个有事业追求的人,可以把“梦”做得高些。虽然开始时是梦想,但只要不停地做,不轻易放弃,就能圆梦。4.圆梦的过程是艰辛的。梦想无论怎样,总潜伏在我们心底,使我们的心境永远得不到宁静,直到这些梦想成为事实。文体上既可以是议论文,也可以是记叙文,还可以写成其他文体。
22.(本小题满分14分)若存在实常数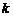 和
和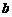 ,使得函数
,使得函数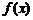 和
和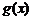 对其定义域上的任意实数
对其定义域上的任意实数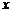 分别满足:
分别满足: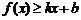 和
和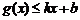 ,则称直线
,则称直线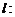
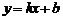 为
为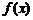 和
和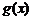 的“隔离直线”.已知
的“隔离直线”.已知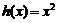 ,
,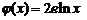 (其中
(其中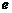 为自然对数的底数).
为自然对数的底数).
(1)求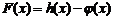 的极值;
的极值;
(2) 函数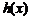 和
和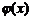 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
福建省泉州七中2010届高三上学期第三次月考
21.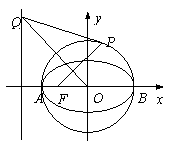 (本小题满分12分)已知圆
(本小题满分12分)已知圆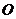 :
: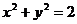 交
交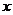 轴于A,B两点,曲线
轴于A,B两点,曲线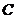 是以AB为长轴,离心率为
是以AB为长轴,离心率为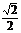 的椭圆,其左焦点为F,若P是圆
的椭圆,其左焦点为F,若P是圆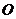 上一点,连结PF,过原点
上一点,连结PF,过原点 作直线PF的垂线交直线x=-2于点Q.
作直线PF的垂线交直线x=-2于点Q.
(Ⅰ)求椭圆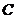 的标准方程;
的标准方程;
(Ⅱ) 当点P在圆 上运动时(不与A、B重合),求证:直线PQ与圆
上运动时(不与A、B重合),求证:直线PQ与圆 相切.
相切.
19.(本小题满分12分)已知正项数列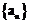 前n项和为
前n项和为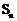 ,首项为
,首项为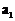 ,且
,且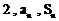 成等差数列。
成等差数列。
(1)求数列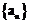 的通项公式;(2)若
的通项公式;(2)若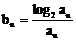 ,
,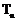 为数列
为数列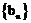 的前n项和,证明
的前n项和,证明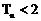 。
。
20(本小题满分12分).
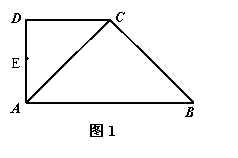
如图1,在直角梯形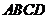 中,
中, 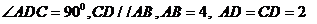 将
将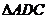 沿
沿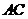 折起,使平面ADC
折起,使平面ADC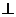 平面ABC,得到几何体D-ABC, 如图2所示.
平面ABC,得到几何体D-ABC, 如图2所示.
(Ⅰ)若E为AD的中点,试在线段CD上找一点F,使EF∥平面ABC,并加以证明;
(Ⅱ)求证: BC⊥平面ACD;
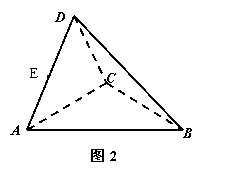 (Ⅲ)求几何体A-BCD的体积.
(Ⅲ)求几何体A-BCD的体积.

18.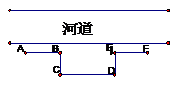 (本小题满分12分)为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为
(本小题满分12分)为了在如图所示的直河道旁建造一个面积为5000m2的矩形堆物场,需砌三面砖墙BC、CD、DE,出于安全原因,沿着河道两边需向外各砌10m长的防护砖墙AB、EF,若当BC的长为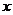 m时,所砌砖墙的总长度为
m时,所砌砖墙的总长度为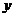 m,且在计算时,不计砖墙的厚度,求
m,且在计算时,不计砖墙的厚度,求
(1)y关于x的函数解析式y=f(x);
(2)若BC的长不得超过40m,则当BC为何值时,y有最
小值,并求出这个最小值.
17、(本小题满分12分)在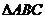 中,角
中,角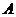 、
、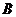 、
、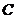 的对边分别为
的对边分别为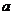 、
、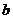 、
、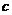 ,且
,且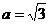 ,
,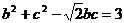 . (Ⅰ)求角
. (Ⅰ)求角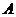 ; (Ⅱ)设
; (Ⅱ)设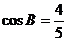 ,求边
,求边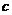 的大小.
的大小.
16.给出下列四个命题:
①设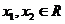 ,则
,则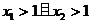 的充要条件是
的充要条件是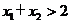 且
且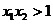 ;
;
②任意的锐角三角形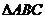 中,有
中,有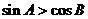 成立;
成立;
③平面上n个圆最多将平面分成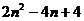 个部分;
个部分;
④空间中直角在一个平面上的正投影可以是钝角.
其中真命题的序号是 (要求写出所有真命题的序号).
15.过椭圆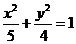 的右焦点作一条斜率为2的直线与椭圆交于
的右焦点作一条斜率为2的直线与椭圆交于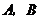 两点,
两点,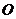 为坐标原点,则
为坐标原点,则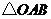 的面积为
.
的面积为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com