1、如何计算4+5+6+7+8+9+10=?

2、如何计算　1+2+3+…+100=(　　 )

　[评述]:　问题<一>为迁移性问题，为引进学习新知识作铺垫， 起温故知新作用；如题1，为说明a1+an=a2+an-1=…，题2则是推导等差数列Sn的方法原型。

　(教师):接下去，同学们看问题<二>与<三>中公式的推导部分。(10分钟)

　问题<二>:

1、在等差数列{an}中，若自然数n、m、p、q，n+m=p+q，则

an、am、ap、aq有关系:(an+am=ap+aq)

2、如何应用等差数列前n项的和公式解题?

　[评述]:　实验教学每节课开始，均以问题形式给出教学目标， 提出学习任务，重点和关键，以利教与学的导向。

　问题<一>:

　现行高考的知识点取于教材，但题型及解题方法在教材中是难见的，就是说对教材全部熟练，高考不一定得到好的成绩，问题系统引导教学法就是针对这个脱节而进行的。实验所编教案本的使用离不开教材，因为教材的解题方法和定义是绝对权威的，而我们所编的教案本是把每节课都问题化，以学生为主体，个个问题让学生动笔动脑，教师只对学生作引导，这样就培养了学生的自学能力，且对学生的负担和教师的工作量大大减轻和减少。下面就我校在高二年级(94级)进行问题系统引导教学法的实验教材(即教案本)作出介绍。因在第一学年实验中，实验教师对教案的一些不足提出了许多宝贵的意见，如:<基础知识复习>， 这课前问题是以填空题出现最好；大题和难题要加一些解答过程；选题量可多而易；……等，在教材编写中，第五章--不等式就当今数学热点问题加入了不等式证明的放缩法和换元法，还加入了柯西不等式的应用，并列举了一些应用题。在数列这章教材中，相应侧重了等差数列和等比数列的混合求和运算，增加了简单的递推数列。在极限这一教学单元中，强调了极限的四则运算，对形如:　

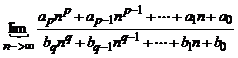　　　　　　 　　　(a_p、b_q不为零，p、 q为整数)

　　　　 Lim　 an - bn

　　 n→∞　 an + bn　　　　 (a、b为正数，且不为1)

　　 这两种极限的运算和讨论作了详细的介绍并补充了习题训练。对数学归纳法的证明以填空形式为主，训练当n=k+1(k∈N)的题型， 并又增加了归纳猜想和证明。在第八章中对复数与《解析几何》的联系作重点详编，复数的模的运算公式，如:

　　　　　　　　　 　　　|z|²= z·z，　|z₁|·|z₂|=|z₁z₂|,

　　　　　　　　　　　　 |z1 + z2|2 + |z1 - z2|2= 2(|z1|2 + |z2|2)

　　　　　　　　　　　　 ||z1| - |z2||≤|z1 ± z2|≤|z1| + |z2|

进行系统分析和运用。第九章排列、组合和二项式定理中主要是开拓视野，用活两个基本原理，题型多而量少。

　我们编写的教案本要求全面地贴近学生和教师的，是为高考而编写的，如92年高考题中有一题是归纳猜想，教材(课本)中是找不到这种题型的，教案本中就要有这类题型的，并且这种教案本是人手一册的，所以在课堂教学中，能增加容量，课前又能作预习辅导材料，课后又能作习题本。

　以下介绍九五年十月二十日在我校举办的一次全市性关于高中数学《问题系统引导教学法实验》一节研讨课，就教案本在实验教学中的特色可“窥见一斑”，并请教于数学界的专家同仁。　课题:“等差数列的前n项的和公式<一>”(高中《代数》 下册P35)

　研讨课题:　如何使用实验教材引导学生系统自我学习、探索、 发现和概括?

　教学过程:

　(教师):今天，我们学习实验教材《数列》 第一章的第五课“等差数列前n项的和公式”，先看学习提要和问题(一)的两个问题；(5分钟)

　　《学习提要》

1、等差数列的前n项的和公式有哪两个形式?是如何导出的?

　中学数学《问题系统引导教学法实验》是一项关于教育思想、教材、教法及课堂结构等方面的综合改革实验，其基本理论是全面落实数学问题系统、目标与检测、自学、情感等四个因素，以扩展数学习题的功能，充分发挥教与学的内在功能，其指导思想是把统编教材转化为一个科学的、生动的、富有启发性和导向性的问题系统组成的、符合该年龄段中学生认知水平和心理水平、直接为教与学服务的实验教材，并由此去转变规范教与学的方法，优化数学教学的基本因素，把数学教学变成数学活动的教学，而不仅仅是活动结果(知识)的教学，实现数学教学“面向全体学生，负担轻，速度快，容量大，效果好”的教学目标。本实验是由柳州地区高中、柳州铁路局一中、柳州钢铁公司一中和柳州教育学院(王为民教授)在1994年8月共同研究决定，在这四校进行此实验， 教学改革实验的中心问题是教材建设问题，是以学生为主体的素质教育问题，因此，我们四校联合并编写了一套高一的《代数》和《立体几何》教案本，在第一年的教改实验中，我们就这套教案本进行了多次的研究教学和观摩教学活动，并把教案本的使用方法传给了高95年级，我校有两个班参加了此项实验，实验的效果颇大，学生和教师都很适应这种教学方法。由于高二要进行会考，加之学校之间学生素质相差太大，有些学校提出实验暂缓进行到高二年级，先在高一年级反复实验几年再说，因此我校高中数学教研组的老师在王为民教授的大力支持下，继续进行此实验，我们编写了高二数学《问题系统引导教学法》教案本(代数本)，并且印刷出来，学生和教师人手一本。在两年的实验中，学生的解题能力和分析能力有很大提高，这得益于实验充分发挥了教与学的内在功能。

2．丁益祥.计算机辅助教学的实践与思考. 《中学数学》1999.11

=3=

　　　　　　　　　　　　　　　　　　　　　　　　 　编号　　　　 号

　　　 　　题目关于高中数学CAI的几点思考

　　　　　　　 单位　 苍南县钱库高级中学　 . 　　　　　　　

　　　　　 作者　　　　　 徐登群　　　　 .　　　　　　　　　　　　　　　　　　　

　　　　　　　 邮编　　　　 325804　　　　　 .

1．周婷.莫把“机灌”变“人灌”. 《中小学教师培训》2000.8

3．注意必要性

CAI可以通过动画多媒体手段向学生模拟演示逼真的现象和过程，提供给学生直观、形象、生动的知识，具有其他媒体不可比拟的优势。在运用CAI时，最好不要将它与普通的媒体(如小黑板、幻灯片)等同用之，要注意运用的必要性。一般来说，教材中难以用言语表达的，学生缺少感情认识而难以领悟的，其他媒体无法呈现的，现场演示条件不足的，介入CAI就能起到画龙点睛的作用，使学生茅塞顿开。例如《球的体积》的教学中，对球体积的推导若以做实验进行说明，时间长、不方便，但若所做实验录成录象播放或用动画制作成课件进行动态演示，可以将这一难点顺利化解。

总之，计算机不可能解决教学中的所有问题，因此夸大CAI的作用，试图以CAI代替传统教学是不现实的。教学过程还是以学生为主体的、教学为主导的活动，师生双边的活动是联接多种教学因素最活跃的因素，是教学过程的主宰，而CAI始终处在辅助性的作用。如何发挥现代科学技术的威力，使计算机在数学教学中起辅助作用，起促进作用是今后研究的重要课题。

　　 参考文献

2．注意辅助性

有些教师在运用CAI过程中，过分夸大其功用，从引入开始，到教学内容，到练习，到练习答案，全由多媒体显现。教师几乎不动用课本，学生基本为接触教材，一切都跟着媒体转，这是违背教学规律的。利用CAI应遵循因材施教的原则，该用则用，为该用则不用，切忌“黑板搬家”，利用CAI还应注意不能整堂课充满影视画面，应该看到过分热闹的画面会分散学生的注意力、会喧宾夺主。因此，CAI应强调注意其辅助性，不管计算机发展到什么程度，它只能辅助教师的教，只能辅助学生的学。如数学例题的讲解，教师不可能知道所有学生的想法和做法，单靠媒体显然不能预料可能会发生的事情，因此有些必要的分析归纳过程和运算推理过程还应通过板书或板演充分地暴露给学生。使计算机在课堂教学中真正体现“辅助”的作用，以确保学生在形象思维与抽象思维、合理推理能力与逻辑推理能力的同步发展。