本节课我们学习了函数的定义(包括定义域、值域的概念)、区间的概念及求函数定义域的方法.学习函数定义应注意的问题及求定义域时的各种情形应该予以重视.(本小结的内容可由学生自己来归纳)

例1求下列函数的定义域.

(1)f(x)＝　　　　　(2)f(x)＝　　　　　(3)f(x)＝+

分析：函数的定义域通常由问题的实际背景确定.如果只给出解析式y＝f(x)，而没有指明它的定义域.那么函数的定义域就是指能使这个式子有意义的实数x的集合.

解：(1)x－2≠0，即x≠2时，有意义

∴这个函数的定义域是{x｜x≠2}

(2)3x+2≥0，即x≥－时有意义

∴函数y＝的定义域是[－，+∞)

(3)

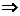
∴这个函数的定义域是{x｜x≥－1}∩{x｜x≠2}＝[－1，2)∪(2，+∞).

注意：函数的定义域可用三种方法表示：不等式、集合、区间.

从上例可以看出，当确定用解析式y＝f(x)表示的函数的定义域时，常有以下几种情况：

(1)如果f(x)是整式，那么函数的定义域是实数集R；

(2)如果f(x)是分式，那么函数的定义域是使分母不等于零的实数的集合；

(3)如果f(x)是偶次根式，那么函数的定义域是使根号内的式子不小于零的实数的集合；

(4)如果f(x)是由几个部分的数学式子构成的，那么函数的定义域是使各部分式子都有意义的实数的集合(即使每个部分有意义的实数的集合的交集)；

(5)如果f(x)是由实际问题列出的，那么函数的定义域是使解析式本身有意义且符合实际意义的实数的集合.

例2　试比较下列两个函数的定义域与值域：

⑴f(x)＝(x－1)²+1,x∈{－1,0,2,3}；

⑵f(x)＝(x－1)²+1,x∈R.

解：⑴函数的定义域为{－1,0,2,3}，

　∵f(－1)＝[(－1)－1]²+1＝5，

同理f(0)＝2，f(1)＝1，f(2)＝2，f(3)＝5，

∴这个函数的值域为{1,2,5}.

⑵∵函数的定义域为R，∴(x－1)²+1≥1，

∴这个函数的值域为{y|y≥1}.

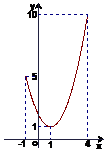
变：f(x)＝(x－1)²+1, x∈[－1，4]

解：画出f(x)＝(x－1)²+1, x∈[－1，4]的图象，

如图所示，得y∈[1,10]

问题十：比较两个函数定义域，你对函数有什么新的认识？

学生练习：P28练习T1,2,3

问题五：如何用集合的观点来阐述上面三个例子中的共同特点？

对于集合A中的任意一个数，按照某种对应关系，集合B中都有惟一的数和它对应.

问题六：如何用集合的观点来理解函数的概念？

结论：函数是建立在两个非空数集之间的单值对应.

反思：⑴结论是否正确地概括了例子的共同特征？

⑵比较上述认识和初中函数概念是否有本质上的差异？

⑶正比例函数，反比例函数，一次函数，二次函数是否也具有上述特征？

问题七：如何用集合的语言来阐述上面三个例子中的共同特点？

对于数集A中的每一个x，按照某种对应关系f，在数集B中都有唯一确定的y和它对应，记作：f：A→B.

函数的定义

设A、B是非空的数集，如果按照某种对应法则f，对于集合A中的任意一个数x，在集合B中都有惟一的元素y和它对应，这样的对应叫做从A到B的一个函数，通常记为

y＝f(x)，x∈A

其中，所有的输入值x组成的集合A叫做函数的定义域.

强调：

⑴集合A与集合B都是非空数集；

⑵对应法则的方向是从A到B；

⑶强调“非空”、“每一个”、“惟一”这三个关键词.

说明：

⑴“单值对应”是函数对应法则的根本特征；

⑵“箭头图”给出了“单值对应”从一个集合到另一个集合的方向性；

⑶“输入”与“输出”的关系.

学生练习P29习题2.1⑴T10

反思：回答问题二、问题三

函数概念用集合、对应的语言叙述后，我们就很容易回答前面所提出的两个问题.

y=1(x∈R)是函数，因为对于实数集R中的任何一个数x，按照对应关系“函数值是1”，在R中y都有惟一确定的值1与它对应，所以说y是x的函数.

Y＝x与y＝不是同一个函数，因为尽管它们的对应关系一样，但y＝x的定义域是R，而y＝的定义域是{x|x≠0}. 所以y＝x与y＝不是同一个函数.

问题九：理解函数的定义，我们应该注意些什么呢？

(教师提出问题，启发、引导学生思考、讨论，并和学生一起归纳、总结)

注意：①函数是非空数集到非空数集上的一种对应.

②符号“f:A→B”表示A到B的一个函数，它有三个要素；定义域、值域、对应关系，三者缺一不可.(定义域→优先，对应法则→核心)

③集合A中数的任意性，集合B中数的惟一性.

④f表示对应关系，在不同的函数中，f的具体含义不一样.

⑤f(x)是一个符号，绝对不能理解为f与x的乘积.

在研究函数时，除用符号f(x)表示函数外，还常用g(x) 、F(x)、G(x)等符号来表示.

若A是函数y＝f(x)的定义域，则对于A中的每一个x，都有一个输出值y与之对应.我们将所有输出值y组成的集合{y|y＝f(x)，x∈A}称做函数的值域.

在现实生活中，我们可能遇到下列问题：

⑴估计人口数量变化趋势是我们制定一系列相关政策的依据.从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如表所示，你能根据这个表说出我国人口变化情况吗？

年　份	1949	1954	1959	1964	1969	1974	1979	1984	1989	1994	1999
人口数/百万	542	603	672	705	807	909	975	1035	1107	1177	1246

⑵一物体从静止开始下落，下落的距离y(m)与下落时间x(s)之间近似地满足关系式y＝4.9x².若一物体下落2s，你能求出它下落的距离吗？

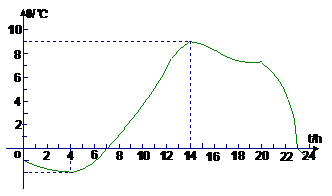⑶下图为某市一天24小时的气温变化图.

①上午6时的气温约是多少？全天的最高、最低气温分别是多少？

②在什么时刻，气温为0℃？

③在什么时刻内，气温在0℃以上？

问题四：在上述例子中，是否确定了函数关系？为什么？

问题一：在初中，我们已经学习了函数的概念，请同学们回忆一下，它是怎样表述的？

(几位学生试着表述，之后，教师将学生的回答梳理，再表述或者启示学生将表述补充完整再条理表述).

设在一个变化的过程中有两个变量x和y，如果对于x的每一个值，y都有惟一的值与它对应，那么就说y是x的函数，x叫做自变量.

我们学习了函数的概念，并且具体研究了正比例函数，反比例函数，一次函数，二次函数，请同学们思考下面两个问题：

问题二：y＝1(x∈R)是函数吗？

问题三：y＝x与y＝是同一个函数吗？

(学生思考，很难回答)

显然，仅用上述函数概念很难回答这些问题，因此，需要从新的高度来认识函数概念(板书课题).

　P20习题2.1⑴7,8,9

能用描点法画出常见函数的图象，并能根据函数的图象解决有关问题

例5　估计人口数量变化趋势是我们制定一系列相关政策的依据.从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如表所示，你能根据这个表说出我国人口变化情况吗？

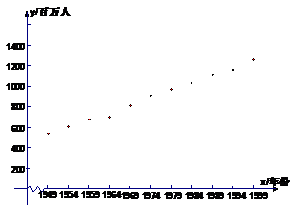
如果把人口数y(百万人)看做年份x的函数，试画出这个函数的图象.

解：由上表的数据，画出的函数图象是11个点.

补：一物体从静止开始下落，下落的距离y(m)与下落时间x(s)之间近似地满足关系式y＝4.9x².若一物体下落2s，你能求出它下落的距离吗？并画出它的图象.

思考：设函数y＝f(x)的定义域为A，则集合P＝{(x,y)｜y＝f(x),x∈A}与集合Q＝{y｜y＝f(x),x∈A}相等吗？请说明理由.

解析：P≠Q，因为P、Q的代表元素不一样，P是点集，Q是值域.

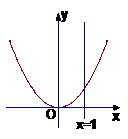
问题：直线x＝1和函数y＝x²+1的图象的公共点可能几个？

解析：根据图象知有且仅有一个公共点.

变：⑴(P29习题6)直线x＝a和函数y＝x²+1的图象的公共点可能几个？

解析：根据图象知有且仅有一个公共点.

⑵直线x＝－1和函数y＝x²+1，x∈[0.+∞)的图象的公共点可能几个？

解析：根据图象知没有公共点.

⑶直线x＝a和函数y＝x²+1，x∈A的图象的公共点可能几个？

解析：当a∈A，则根据图象知有且仅有一个公共点；当a∉A时，没有公共点.

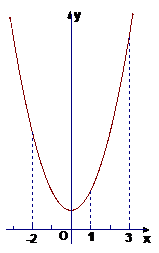
例6　试画出函数f(x)＝x²+1的图象，并根据图象回答下列问题：

⑴比较f(－2),f(1),f(3)的大小；

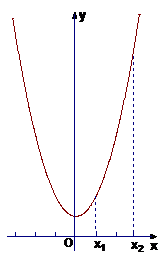⑵若0＜x₁＜x₂,试比较f(x₁)与f(x₂)的大小.

解：函数的图象如下[来源:]

⑴根据图象知

f(3)＞f(－2)＞f(1),

⑵根据图象知，当0＜x₁＜x₂时，

f(x₁)＜f(x₂).

思考：在上例⑵中，

⑴如果把“0＜x₁＜x₂”改为

“x₁＜x₂＜0”，那么f(x₁)与f(x₂)

哪个大？

⑵如果把“0＜x₁＜x₂”改为

“|x₁|＜|x₂|”，那么f(x₁)与f(x₂)

哪个大？

解析：仍然根据函数的图象，有

⑴f(x₁)＞f(x₂).

⑵∵f(x)的图象关于y轴对称，∴当|x₁|＜|x₂|时有f(x₁)＜f(x₂).

学生练习P28练习1,2,3

将自变量的一个值x₀作为横坐标，相应的函数值f(x₀)作为纵坐标，就得到坐标平面上的一个点(x₀,f(x₀)).当自变量取遍函数定义域A中的每一个值时，就得到一系列这样的点.所有这些点组成的集合(点集)为

　　　{(x,f(x))｜x∈A}，

即

　　　　　{(x,f(x))｜y＝f(x),x∈A}，

所有这些点组成的图形就是函数y＝f(x)的图象.

在初中，我们已学过函数的图象，并能作出函数y＝2x－1，y＝(x≠0)以及y＝x²的图象.社会生活中还有许多函数图象的例子，如心电图、示波图等.

回想一下，在初中我们是采用什么方法来画出函数的图象？

描点法

描点法作图的步骤有哪些？

列表、描点、连线

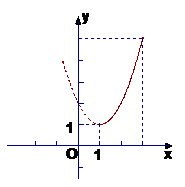
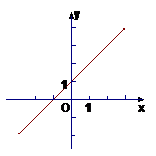
练习(P25例4)试画出下列函数的图象：

⑴f(x)＝x+1

⑵f(x)＝(x－1)²+1,x∈[1,3)