
22. 一种填数字彩票2元一张,购买者在卡上依次填上0~9中的两个数字(允许重复).中奖规则如下:如果购买者所填的两个数字依次与开奖的两个有序数字分别对应相等,则中一等奖10元;如果购买者所填的两个数字中,只有第二个数字与开奖的第二个数字相等,则中二等奖2元;其他情况均无奖金.
(1)小明和小辉在没有商量的情况下各买一张这种彩票,求他俩都中一等奖的概率;
(2)求购买一张这种彩票中奖的概率;
(3)设购买一张这种彩票的收益为随机变量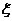 ,求
,求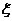 的数学期望.
的数学期望.
21.[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
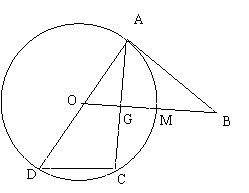 A.[选修4-1:几何证明选讲]如图,已知
A.[选修4-1:几何证明选讲]如图,已知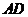 为圆O的直径,直线
为圆O的直径,直线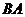 与圆O相切于点
与圆O相切于点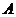 ,直线
,直线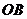 与弦
与弦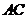 垂直并相交于点
垂直并相交于点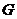 ,与弧
,与弧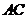 相交于
相交于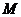 ,连接
,连接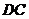 ,
,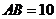 ,
,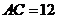 .
.
(1)求证: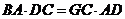 ;
;
(2)求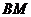 .
.
B.[选修4-2:矩阵与变换]矩阵与变换:给定矩阵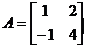 .
.
试求矩阵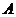 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C.[选修4-4:坐标系与参数方程]已知直线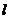 的参数方程:
的参数方程: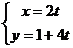 (
(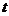 为参数),曲线C的极坐标方程:
为参数),曲线C的极坐标方程: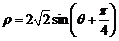 ,求直线
,求直线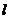 被曲线C截得的弦长.
被曲线C截得的弦长.
D.[选修4-5:不等式选讲]
设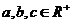 ,求证:
,求证: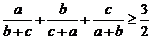 .
.
[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
20. (本小题16分)已知数列 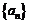 和
和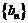 满足
满足 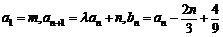
(1)当m=1时,求证:对于任意的实数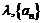 一定不是等差数列;
一定不是等差数列;
(2)当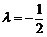 时,试判断
时,试判断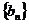 是否为等比数列;
是否为等比数列;
连云港市数学试题附加题
(考试时间:30分钟;满分:40分)
19. (本小题16分)已知函数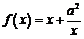 ,
,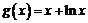 ,其中
,其中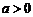 .
.
(1)若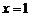 是函数
是函数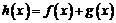 的极值点,求实数
的极值点,求实数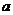 的值;
的值;
(2)若函数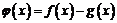 在
在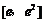 (
(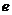 为自然对数的底数)上存在零点,求实数
为自然对数的底数)上存在零点,求实数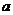 的取值范围.
的取值范围.
(3)若对任意的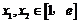 都有
都有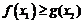 成立,求实数
成立,求实数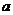 的取值范围.
的取值范围.
18. (本小题15分)在平面直角坐标系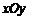 中 ,已知以
中 ,已知以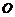 为圆心的圆与直线
为圆心的圆与直线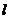 :
: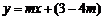 ,
,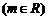 恒有公共点,且要求使圆
恒有公共点,且要求使圆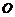 的面积最小.
的面积最小.
(1)写出圆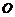 的方程;
的方程;
(2)圆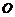 与
与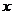 轴相交于A、B两点,圆内动点P使
轴相交于A、B两点,圆内动点P使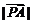 、
、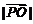 、
、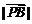 成等比数列,求
成等比数列,求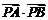 的范围;
的范围;
(3)已知定点Q(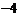 ,3),直线
,3),直线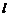 与圆
与圆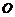 交于M、N两点,试判断
交于M、N两点,试判断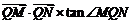 是否有最大值,若存在求出最大值,并求出此时直线
是否有最大值,若存在求出最大值,并求出此时直线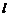 的方程,若不存在,给出理由.
的方程,若不存在,给出理由.
17. (本小题15分)如图,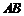 为圆
为圆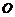 的直径,点
的直径,点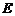 、
、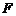 在圆
在圆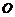 上,且
上,且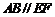 ,矩形
,矩形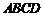 所在的平面和圆
所在的平面和圆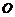 所在的平面互相垂直,且
所在的平面互相垂直,且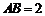 ,
,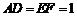 .
.
 (1)求证:
(1)求证: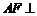 平面
平面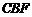 ;
;
(2)设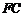 的中点为
的中点为 ,求证:
,求证: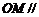 平面
平面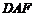 ;
;
(3)设平面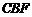 将几何体
将几何体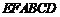 分成的两个锥体的
分成的两个锥体的
体积分别为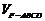 ,
,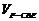 ,求
,求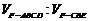 .
.
16. (本小题14分)已知关于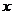 的一元二次函数
的一元二次函数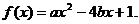
(1)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为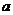 和
和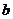 ,求函数
,求函数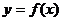 在区间[
在区间[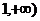 上是增函数的概率;
上是增函数的概率;
(2)设点(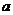 ,
,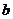 )是区域
)是区域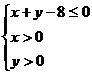 内的随机点,求函数
内的随机点,求函数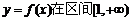 上是增函数的概率.
上是增函数的概率.
15.(本小题14分)已知向量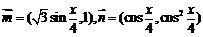 .
.
(1)若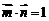 ,求
,求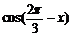 的值;
的值;
(2)记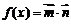 ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足
(2a-c)cosB=bcosC,求函数f(A)的取值范围.
14. 在正整数数列中,由1开始依次按如下规则将某些数染成红色,先染 1,再染2个偶数2、4;再染4后面最邻近的3个连续奇数 5、7、9;再染 9 后面最邻近的4个连续偶数 10、12、14、16;再染此后最邻近的5个连续奇数17、19、21、23、25. 按此规则一直染下去,得到一红色子数列 1,2,4,5,7,9,12,14,16,17,…. 则在这个红色子数列中,由1开始的第2009个数是 .
13. 设函数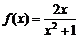 ,
,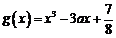 ,若对于任意
,若对于任意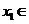
 ,总存在
,总存在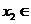
 ,使得
,使得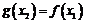 成立.则正整数a的最小值为 .
成立.则正整数a的最小值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com