
6、三角形内切圆以及三角形内心的概念。
5、圆的切线的性质 和判定 。
4、直线和圆的位置关系。
3、圆与相似三角形、全等三角形、三角函数的综合题。
2、求线段与角和弧的度数。
1、理解圆的基本概念与性质。
6、 牢固掌握二次函数的概念和性质,注重在实际情景中理解二次函数的意义,关注与二次函数相关的综合题,弄清知识之间的联系。
例题精讲
例1、在平面直角坐标系中,点(-1,-2)所在的象限是 ( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
分析:考查已知的点的坐标,确定它的象限
答案:D
例2 .如果代数式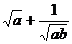 有意义.那么直角坐标系中点A(a、b)的位置在( ).
有意义.那么直角坐标系中点A(a、b)的位置在( ).
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
分析:要使根式有意义,a和b都要大于0
答案: A
例3、如图2,直线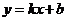 与
与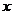 轴交于点(-4 , 0),则
轴交于点(-4 , 0),则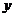 > 0时,
> 0时,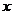 的取值范围是 ( )
的取值范围是 ( )
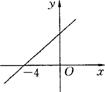 A、
A、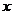 >-4 B、
>-4 B、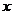 >0 C、
>0 C、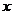 <-4 D、
<-4 D、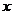 <0
<0
分析:考查一次函数图像
答案:A
例4.某班同学在探究弹簧的长度跟外力的变化关系时,实验记录得到的相应数据如下表:
|
砝码的质量x(克) |
0 |
50 |
100 |
150 |
200 |
250 |
300 |
400 |
500 |
|
指针位置y(厘米) |
2 |
3 |
4 |
5 |
6 |
7 |
7.5 |
7.5 |
7.5 |
则y关于x的函数图象是( ).D
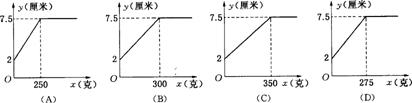
分析:当砝码的质量大于或等于275克时,指针位置7.5(厘米)不变
答案:D
例5.你知道吗?平时我们在跳大绳时,绳甩到最高处的形状可近似地看为抛物线.如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为4 m,距地面均为1m,学生丙、丁分别站在距甲拿绳的手水平距离1m、2.5 m处.绳子在甩到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为(建立的平面直角坐标系如右图所示)
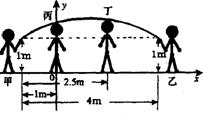 ( )
( )
A.1.5 m B.1.625 m C.1.66 m D.1.67 m
分析:本题考查二次函数的应用
答案:B
例6. 下列四个图象中,不表示某一函数图象的是( ).
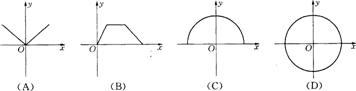
分析:D图不能用函数式表示出来。
答案:D
例6下列函数中,正比例函数是( )
A.y==-8x B.y==-8x+1 C.y=8x2+1
D.y=-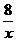
分析:A是正比例函数,B是一次函数,C是二次函数,D是反比例函数
答案:A
例7.一个矩形的面积是6,则这个矩形的一组邻边长x与y的函数关系的图像大致是 ( )
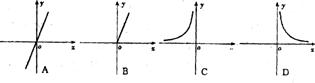
分析:XY=6 函数式为反比例函数,且X>0 Y>0,图像在第一象限
答案:D
例8.已知:关于x的一元二次方程ax2+bx+c=3的一个根为x=-2,且二次函数y=ax2+bx+c的对称轴是直线x=2,则抛物线的顶点坐标为( )
A(2,-3) B.(2,1) C(2,3) D.(3,2)
答案:C
例9.已知直线y=kx+b与双曲线y=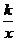 交于A(x1,y1),,B(x2,y2)两点,则x1·x2的值( )
交于A(x1,y1),,B(x2,y2)两点,则x1·x2的值( )
A.与k有关、与b无关 B.与k无关、与b有关
C.与k、b都有关 D.与k、b都无关
答案:D
例10.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,O)、(x1,0),且1<x1<2,与y轴的正半轴的交点在点(O,2)的下方.下列结论:①a<b<0;②2a+c>O;③4a+c<O;④2a-b+1>O,其中正确结论的个数为( )
A 1个 B. 2个 C. 3个 D.4个
答案:D
例11.函数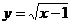 中,自变量x的取值范围是___________________;
中,自变量x的取值范围是___________________;
答案:x≥l
例12、大连市内与庄河两地之间的距离是160千米,若汽车以平均每小时80千米的速度从大连市内开往庄河,则汽车距庄河的路程y (千米)与行驶的时间x (小时)之间的函数关系式为_________________________;
答案:y=-80x+160
例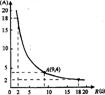 13.某蓄电池的电压为定值,右图表示的是该蓄电池电流I(A)与电阻R(Ω)之间的函数关系图像.请你写出它的函数解析式是 .
13.某蓄电池的电压为定值,右图表示的是该蓄电池电流I(A)与电阻R(Ω)之间的函数关系图像.请你写出它的函数解析式是 .
答案:I=36/R
例14.如图,Rt△ABO的顶点A是双曲线y=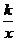 与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B,且S△ABO=
与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B,且S△ABO=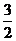 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标和△AOc的面积.
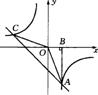
解:(1)设A点坐标为(x,y),S△ABO=3/2
k=±3,∵点A在第四象限内,∴k=-3,.反比例函数的解析式为y=-3/x,一次函数的解析式为y=-x-2; (2) 解两个解析式的方程组得x1=-3 y1=1 x2=1 y2=-3.A点坐标为(1,-3),C点坐标为(-3,1),设直线AC与y轴交于点D,则D点坐标为(O,-2),S△AOC=S△AOD+S△COD=4(平方单位).
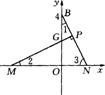
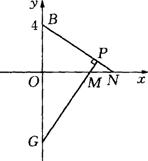
例15.在直角坐标系xOy中,O为坐标原点,A,B,C三点的坐标分别为A(5,0),B(0,4),C(-1,0).点M和点N在x轴上(点M在点N的左边),点N在原点的右边,作MP⊥BN,垂足为P(点P在线段BN上,且点P与点B不重合),直线MP与y轴交于点G,MG=BN.
(1)求经过A,B,C三点的抛物线的解析式;(2)求点M的坐标;
(3)设ON=t,△MOG的面积为s,求s与t的函数关系式,并写出自变量t的取值范围;
(4)过点B作直线BK平行于x轴,在直线BK上是否存在点R,使△ORA为等腰三角形,若存在,请说明理由.
解:(1)所求的解析式为y=x2+x+4;
(2)依题意,分两种情况:①当点M在原点的左边(如图1)时,在Rt△BON中,∠1+∠3=90°,MP⊥BN,∴∠2+∠3 ∠BON=∠MOG=90°∴∠1=∠2,在Rt△BON和Rt△MOG中,.Rt△BON≌Rt△MOG,OM=OB=4,∴M点坐标为(-4,O). ②当点M在原点的右边(如图2)时,同理可证:OM=OB=4,此时M点坐标为(4,O) M点坐标为(4,0)或(-4,O);
(3)图1中,Rt△BON≌Rt△MOG,∴OG=ON=t,∴s=2t(其中0<t<4),图2中,同理可得s=2t,其中t>4,.所求的函数关系式为S=2t,t的取值范围为t>0且t≠4;
(4)存在点R,使△ORA为等腰三角形,其坐标为:R1(-3,4),R2(3,4),R3(2,4),R4(5/2,4),R5(8,4).
例16.已知:二次函数y=ax2-(b+1)x-3a的图象经过点P(4,10),交x轴于A(x1,O),B(x2,O)两点(x1<x2),交y轴负半轴于C点,且满足3AO=OB.(1)求二次函数的解析式;(2)在二次函数的图象上是否存在点M,使锐角∠MCO>∠ACO?若存在,请你求出M点的横坐标的取值范围;若不存在,请你说明理由.
(1)解:如图∵抛物线交x轴于点A(x1,0),B(x2,O),
则x1·x2=3<0,又∵x1<x2,
∴x2>O,x1<O,∵30A=OB,∴x2=-3x1.
∴x1·x2=-3x12=-3.∴x12=1.
x1<0,∴x1=-1.∴.x2=3.
∴点A(-1,O),P(4,10)代入解析式得解得a=2 b=3
∴.二次函数的解析式为y-2x2-4x-6.
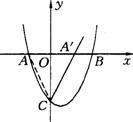
(2)存在点M使∠MC0<∠ACO.
(2)解:点A关于y轴的对称点A’(1,O),
∴直线A,C解析式为y=6x-6直线A'C与抛物线交点为(0,-6),(5,24).
∴符合题意的x的范围为-1<x<0或O<x<5.
当点M的横坐标满足-1<x<O或O<x<5时,∠MCO>∠ACO.
5、 明确反比例函数的特征图像,提高实际应用能力。
4、 掌握一次函数的增减性、分布象限,会作图
3、 掌握一次函数的一般形式和图像
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com