
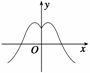
2.如果函数y=f(x)的图象如图所示,那么导函数y=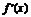 的图象可能是 ( )
的图象可能是 ( )
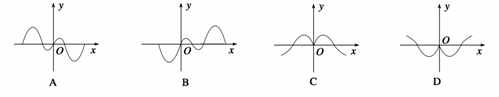
1.曲线y=ex在点(2,e2)处的切线与坐标轴所围三角形的面积为( )
?A.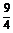 e2?
B.2e2
C.e2
D.
e2?
B.2e2
C.e2
D.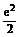
21.(本大题满分14分)
奇函数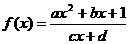 (
(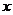 ≠0,
≠0,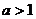 ),且当
),且当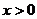 时,
时,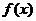 有最小值
有最小值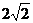 ,又
,又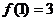 。
。
(1)求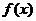 的表达式;
的表达式;
(2)正整数列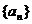 中,
中,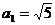 ,
,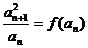 ,求数列
,求数列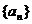 的通项公式;
的通项公式;
(3)对(2)中的数列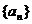 ,若
,若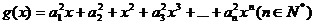 ,求函数
,求函数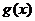 在
在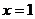 处的导数
处的导数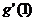 ,并比较
,并比较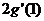 与
与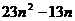 的大小
的大小
20.(本大题满分13分)
已知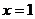 是函数
是函数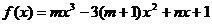 的一个极值点,其中
的一个极值点,其中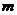 、
、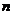 ∈R,
∈R,
m≤0。
(1)求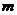 与
与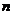 的关系表达式;
的关系表达式;
(2)求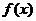 的单调区间;
的单调区间;
(3)当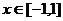 时,函数
时,函数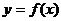 的图象上任意一点的切线的斜率恒大于3m,求m的取值范围。
的图象上任意一点的切线的斜率恒大于3m,求m的取值范围。
19.(本大题满分12分)
已知函数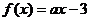 ,
,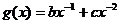 (
(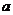 、
、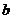 、
、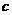 ∈R),且
∈R),且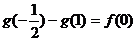 .
.
(1)试求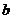 、
、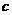 所满足的关系式;
所满足的关系式;
(2)若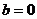 ,方程
,方程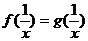 在(0,+∞)有唯一解,求
在(0,+∞)有唯一解,求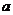 的取值范围。
的取值范围。
(3)若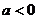 ,
,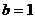 ,集合
,集合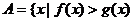 ,且
,且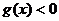 ,
, 试求集合A。
试求集合A。
18.(本大题满分12分)
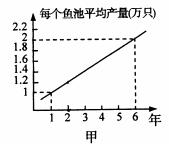
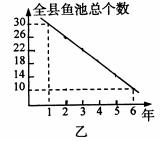
甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图。请你根据提供的信息说明:
(1)第2年全县鱼池的个数及全县出产的鳗鱼总数;
(2)到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了?说明理由;
(3)哪一年的规模(即总生产量)最大?说明理由。
17.(本大题满分12分)
已知向量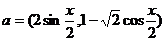 ,
,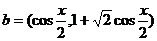 ,
,
函数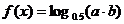
(1)求函数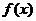 的定义域和值域
的定义域和值域
(2)求函数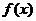 的单调区间。
的单调区间。
16.(本大题满分12分)
设集合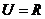 ,函数
,函数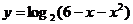 的定义域为A,函数
的定义域为A,函数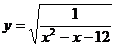 的定义域为B。
的定义域为B。
(1)求集合A与B;
(2)求A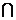 B、(CUA)∪B。
B、(CUA)∪B。
15.等差数列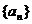 中首项为
中首项为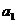 ,公差为
,公差为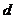 ,前
,前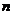 项和为
项和为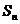 ,给出下列四个命题:
,给出下列四个命题:
①数列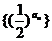 为等比数列; ②若
为等比数列; ②若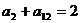 ,则
,则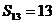 ;
;
③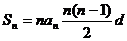 ; ④若
; ④若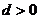 ,则
,则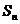 一定有最大值;
一定有最大值;
其中正确命题的序号是 。
14.不等式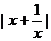
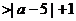 对于一切非零实数
对于一切非零实数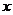 均成立,则实数
均成立,则实数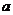 的取值范围是 。
的取值范围是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com