
2.等差数列{an}的前n项的和为Sn,且公差d=3,S2=4,则S4的值为
A.10 B.11 C.13 D.20
1.复数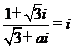 ,则实数α的值为
,则实数α的值为
A.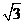 B.-
B.-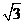 C.1
D.-1
C.1
D.-1
9.解: (1)由已知, 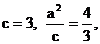 ∴
∴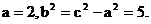
所以求双曲线C的方程为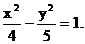
(2)设P的坐标为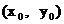 , M, N的纵坐标分别为
, M, N的纵坐标分别为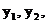
∵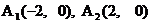 , ∴
, ∴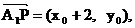
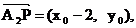
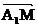
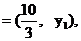
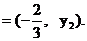
∵ 与
与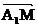 共线, ∴
共线, ∴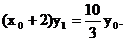
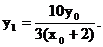
同理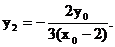 …………(8分)
…………(8分)
∵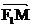
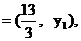
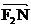
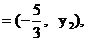
∴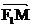 ·
·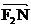 =
=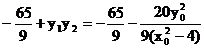
=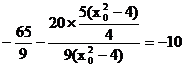
9.如图, 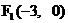 ,
, 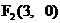 是双曲线C的两焦点, 直线
是双曲线C的两焦点, 直线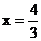 是双曲线C的右准线, A1,
A2双曲线C的两个顶点, 点P是双曲线C右支上异于A2的一动点, 直线A1P,A2P交双曲线C的右准线分别于M, N两点.
是双曲线C的右准线, A1,
A2双曲线C的两个顶点, 点P是双曲线C右支上异于A2的一动点, 直线A1P,A2P交双曲线C的右准线分别于M, N两点.
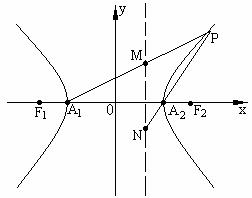 (1) 求双曲线C的方程;
(1) 求双曲线C的方程;
(2) 求证: 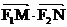 是定值.
是定值.
8.证明:(1)连结AQ1,因为Q与Q1关于x轴对称,而A在x轴上
则在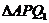 中,AB平分
中,AB平分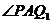
由内角平分线定理可知: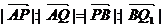
而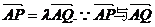 同向,故
同向,故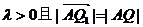
则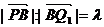 ,又P、B、Q1在同一直线且
,又P、B、Q1在同一直线且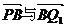 同向
同向
于是有: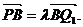
(2)设过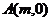 的直线l与椭圆C:
的直线l与椭圆C: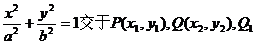 与Q关于x轴对称,则
与Q关于x轴对称,则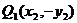
由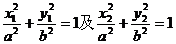 相减得
相减得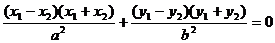
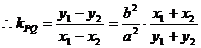 PQ直线方程:
PQ直线方程: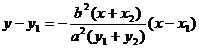
而PQ过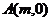 ,则有:
,则有: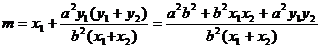
而PQ1过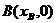 ,同理可求得:
,同理可求得: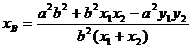
下面利用分析法证明: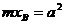 ,
,
即证: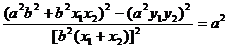 ……………………①
……………………①
只需证: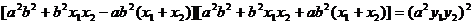
只需证: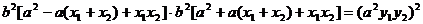
即证: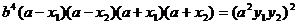 ………………②
………………②
而(x1,
y1)在椭圆上,则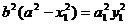 ………………③
………………③
同理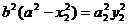 ……………………………………④
……………………………………④
由③×④可知②成立,从而①式得证.因此mxB=a2成立.
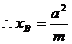 ∴点B为一定点
∴点B为一定点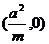 。
。
另法:证(1)设l直线过A(m,0)和椭圆交于P(x1,y1),Q(x2, y2),而Q1与Q关于x轴对称,则Q1(x1, -y2)
由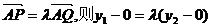
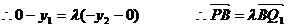 …………………………(6分)
…………………………(6分)
(2)由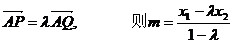 …………………………①
…………………………①
由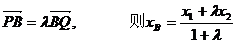 …………………………②
…………………………②
由①×②得 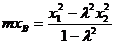 ………………………………③
………………………………③
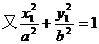 ……………………………………………………④
……………………………………………………④
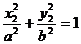
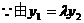 ,由④-⑤·
,由④-⑤·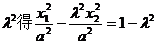
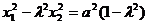
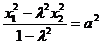 ……………………⑥
……………………⑥
由③⑥可知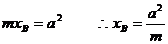 ,∴点B为一定点
,∴点B为一定点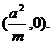
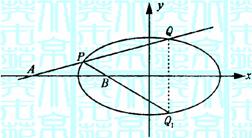
8.过椭圆C: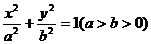 外一定点
外一定点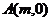 作一直线
作一直线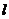 交椭圆C:于P、Q两点,又Q关于x轴对称点为Q1,连结PQ1交x轴于B点.
交椭圆C:于P、Q两点,又Q关于x轴对称点为Q1,连结PQ1交x轴于B点.
(1)若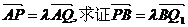 .
.
 (2)求证:点B为一定点
(2)求证:点B为一定点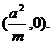
7.解:(I)由已知,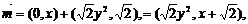
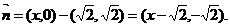
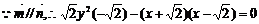
即所求曲线的方程是: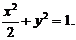
(Ⅱ)由(I)求得点M(0,1),显然直线l与x轴不垂直,
故可设直线l的方程为y=kx+1.
由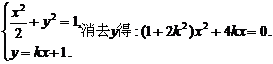
解得x1=0, x2=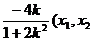 分别为M,N的横坐标).
分别为M,N的横坐标).
由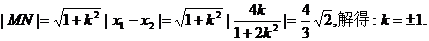
所以直线l的方程x-y+1=0或x+y-1=0.
7.已知向量m1=(0,x),n1=(1,1),m2=(x,0),n2=(y2,1)(其中x,y是实数),
又设向量m=m1+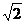 n2,n=m2-
n2,n=m2-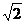 n1,且m//n,点P(x,y)的轨迹为曲线C.
n1,且m//n,点P(x,y)的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)设曲线C与y轴的正半轴的交点为M,过点M作一条直线l与曲线C交于另一点N,当|MN|=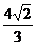 时,求直线l的方程.
时,求直线l的方程.
6. 解:由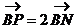 知点N为BP中点
知点N为BP中点
由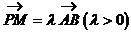 知
知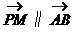 且点M与B位于
且点M与B位于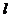 同侧
同侧
∵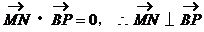
由此知MN为线段BP的垂直平分线,所以应有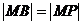
由抛物线定义知点M的轨迹为抛物线,点B为焦点,直线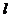 为准线
为准线
(I)因为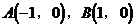 ,所以
,所以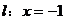
抛物线方程为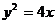 ,即为点M的轨迹方程
,即为点M的轨迹方程
(II)存在点Q,即为焦点B(1,0)
先证明如下:设EF为抛物线的焦点弦,设其中点为H,分别由E、H、F向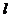 作垂线,垂足分别为R、S、T。
作垂线,垂足分别为R、S、T。
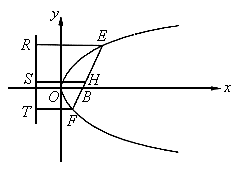
由梯形的中位线知:
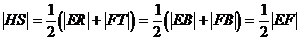
即以EF为直径的圆的圆心到直线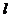 的距离等于半径。
的距离等于半径。
所以以EF为直径的圆必与直线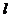 相切。
相切。
所以,存在点Q,其坐标为(1,0)。
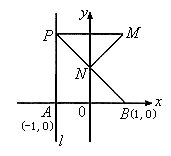
6. 如图所示,已知A(-1,0),B(1,0),直线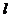 垂直AB于A点,P为
垂直AB于A点,P为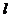 上一动点,点N为线段BP上一点,且满足
上一动点,点N为线段BP上一点,且满足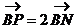 ,点M满足
,点M满足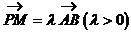 ,
,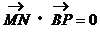 。
。
(I)求动点M的轨迹方程C;
(II)在上述曲线内是否存在一点Q,若过点Q的直线与曲线C交于两点E、F,使得以EF为直径的圆都与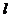 相切。若存在,求出点Q的坐标。若不存在,请说明理由。
相切。若存在,求出点Q的坐标。若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com