3.解决不等式(组)的应用题，要求学生会将应用题里关于‘已 知 量 ’‘未知 量 ’之间的关系用明确的不等式关系表示出来，并注意 应用题中字母 所表示的实际意义。

中考将会以填空和选择的方式考查不等式的基本性质和解集概念，解答题是解不等式(组)，并把解集在数轴上表示出来。不等式的应用题还是热点考查内容，考查可能与日常生活相联系，也可能与其他章节内容，如方程、函数及几何内容相结合。

应试对策

解不等式(组)是本 节 的重点，而不等式的性质是解不等式的基础，在复习本节 时 ，首先要强化三条性质的应用顺练，切忌不等式两边同乘 (除)含 字母的代数式(即正负不明的代数式)；其次注意 数 形 结合的方法，即充分利用数轴，关于不等式(组)的应用题，要通过建模训练，学会找出实际问题中的不等关系，并能在不等式的解集中找出符合题意的答案，还要注意与其他类型的应用题结合起来训练。

例题精讲

例1.函数y=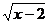中，自变量x的取值范围是(　　 )

A．x≠2　 B．x≥2 C.x≤2D．x>2

分析：通过不等式的形式2算术平方根中被开方数的非负性。

答案：B

例2．不等式2x+1≥5的解集在数轴上表示正确的是　　 (　　 )

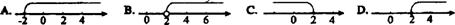
分析：考查不等式求解和用数轴表示其解集。注意取实心点的条件，不等式的解为x≥2

答案：D

例3．不等式组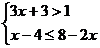的最小整数解是　　　　　　　 (　　 )

　　 A．0　　　　　　　 B．1　　　　　　　 C．2　　　　　　　 D．－1

分析：整数包括正整数、负整数和0

答案：A

例4.不等式组　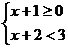 　的整数是(　　 )

(A) -1，0，1　　　　　 (B) -1，1　　　　　 (C) -1，0　　　　　 　 (D) 0，1

答案：C

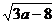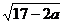例5.如果最简二次根式与是同类根式，那么使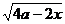有意义的x的取值范围是　 (　　 )

　 A．x≤10　　 B．x≥10　　 C．x<1O D．x>10

分析：考查同类根式的意义及二次根式有意义的条件。

答案：A

例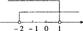6.如图，数轴上表示的一个不等式组的解集，这个不等式组的整数解是__________。

分析：考查不等式求解和用数轴表示其解集。注意取实心点的条件

答案：-1，0

例7.我市某中学要印制本校高中招生的录取通知书，有两个印刷厂前来联系制作业务，甲厂的优惠条件是：按每份定价1．5元的八折收费，另收900元制版费；乙厂的优惠条件是：每份定价1．5元的价格不变，而制版费900元则六折优惠．且甲乙两厂都规定：一次印刷数量至少是500份．

　 (1)分别求两个印刷厂收费y(元)与印刷数量x(份)的函数关系，并指出自变量x的取值范围．

　 (2)如何根据印刷的数量选择比较合算的方案?如果这个中学要印制2000份录取通知书。那么应当选择哪一个厂?需要多少费用?

分析：本题主要考查一次函数、不等式等知识，考查运算能力及分析和解决实际问题

　 的能力．

解：(1)y_甲=1．2x+900(元)x≥500(份)，且x是整数

y_乙=1．5x+540(元)　 x≥500(份)，且x是整数

(2)

若y_甲>y_乙，即1．2x+900>1．5x+540∴x<1200

若y_甲=y_乙，即 1．2x+900=1．5x+540∴x=1200

若y_甲<y_乙，即1．2x+900<1．5x+540∴x>1200

当x=2000时，y_甲=3300

答：当500≤x<1200份时，选择乙厂比较合算；　　

当x=1200份时，两个厂的收费相同；　　

当x>1200份时，选择甲厂比较合算；

所以要印2000份录取通知书，应选择甲厂，费用是3300元．

2.不等式的基本性质，一元 一次不等式(组)解法以及解集的数轴表示。

1.不等式，一元 一次不等式(组) 及其解集的概念。

3、理解梯形、直角梯形的有关概念，会进行有关计算，掌握等腰梯形的性质与判别方法的应用，熟练其辅助线的添法 ，体会转化的思想。

例题精讲

例1.如图，在□ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE．则BF的长是(　　 )．

(A)5　　 (B)8．2　 (C)6．4　　 (D)1．8　　　

答案：D

例2.顺次连结矩形各边中点所得的四边形是　　　　 (　　 )

　 A．等腰梯形　　 B．正方形　　 C．菱形　　 D．矩形

答案：C

例3.矩形ABCD中，M是BC的中点，且MA⊥MD，若矩形的周长为48 cm，则矩形ABCD的面积为　　 　　cm²．128

答案：128

例4.如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AC将梯形分成两个三角形，其中△ACD是周长为18 cm的等边三角形，则该梯形的中位线的长是(　　 )．

(A)9 cm　　 (B)12cm　　 (c)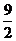cm　　 (D)18 cm

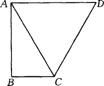答案：C　　　　　　　　　　　　　　　　　　　　

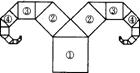例5.如图，是一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②’，…，依此类推，若正方形①的边长为64 cm，则正方形⑦的边长为　　　　 cm．

答案：8

例6.为美化烟台，市政府下大气力实施城市改造，今春改造市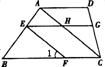区主要街道，街道两侧统一铺设长为20厘米，宽为10厘米的长方形水泥砖，若铺设总面积为10．8万平方米，那么大约需水泥砖　　　　 块(用科学记数法表示)．

答案：5.4×10⁶

例7.如图，AD∥EG∥BC，AC∥EF，则图中与∠1相等的角(不含∠1)有　　　　 个；若∠1=50°，则∠AHG=　　　

答案：5,130°

例8.如图，已知□ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F，与AC相交于点O．

求证：四边形AFCE是菱形．

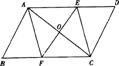
证明：四边形ABCD是平行四边形　　 ∴AE∥FC

　 ∴∠FAO=∠FCO　 ∵EF垂直平分AC

　 ∴OA=OC　 AE=CE　 又∵∠AOE=∠COF

　　 ∴△AOE≌△COF　　 ∴．AE=FC　　 AE∥FC

　 ∴四边形AFCE是平行四边形

　 又∵AE=CE　 □AFCE是菱形 　　

例9：如图，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．

求证：BF=2CF．

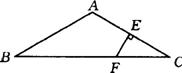
证明：连结AF．∵EF是AC的垂直平分线，∴AF=FC．∵AB=AC，

∠BAC=120°，∠B=∠C=30°．∠BAF=90°.AF=BF/2．　 即BF=2AF．∴BF=2CF．

例10.如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F．

(1)求证：DE=DF．　　

(2)只添加一个条件，使四边形EDFA是正方形．请你至少写出两种不同的添加方法．(不另外添加辅助线，无需证明)

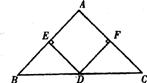
解：(1)∵DE⊥AB，DF⊥AC∵．∠DEB=∠DFC=90°

　　 ∵AB=AC，∴∠B=∠C．又DB=DC，

　 △DEB≌△DFC(AAS)　　 ∴DE=DF．　　

．　 (2)∠A=90°；四边形AFDE是平行四边形等

　　 (方法很多，如∠B=45°或BC=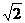AB或DE⊥DF或F为AC中点或DF∥AB等)

2、掌握矩形、菱形、正方形的相关性质和判别方法，进行证明和计算，要注意培养数形结合的能力，灵活运用知识解决综合性问题的能力。

1、熟记多边形的内角和公式、外角和公式，会利用公式求多边形的边数理解平行四边形的面积、周长、对称性，掌握平行四边形的性质。

9、等腰梯形的定义性质及判别方法的应用

中考将继续考查多边形的内、外角和公式的应用，平行四边形的性质和判别方法的应用，考查特殊平行四边形的性质与判别方法，其中菱形、矩形、正方形的性质与判别将是考查的重点，关注特殊四边形与函数类问题结合的题型。将继续考查梯形有关的计算与证明，其中等腰梯形的性质与判别方法的应用是考查的重点。

应试对策

8、梯形、直角梯形的定义及应用。

7、平行四边形是矩形、菱形、正方形的条件的应用。

6、平行四边形、矩形、菱形、正方形的关系。