
[命题特点]:
(l)重点考查的考点有:我国的民族关系、民族原则和民族政策,我国的宗教政策,科学世界观与封建迷信的区别,国际关系及其决定因素,和平与发展,国际新秩序,国际竞争的实质,我国的外交活动和外交政策。
(2)命题题型情况:① 我国的民族和宗教一般以选择题为主,偶有主观题出现,主观题主要表现在文字上,与历史、地理结合出题。② 我国的对外政策题型主要以选择题、简答题和分析说明题为主。主观题要重点把握国际关系及其决定因素与独立自主的和平外交政策。试题具有时政性和开放性,侧重于考查考生对时事政治的理解和创造性思维的能力,试题要求发散性思维,知识既在书本上又在书本外,所以做好这类题目就需要在平时的学习中注意对知识的积累,不能读死书。
[应对策略]
复习本专题时既要注重对知识结构的把握,又要学会运用基本理论分析相关的热点问题。
(l)民族宗教问题要注意民族关系、民族原则、民族政策、宗教政策的有机统一。重点把握民族关系的原则、民族区域自治和宗教信仰自由两大政策。国际关系和我国的对外政策问题要注意把握国际关系的决定因素及其构成是什么,包括主权国家、联合国及国际组织以及作为纽带准则的国际法;国际社会的状况(怎么样),包括和平与发展、国际新旧秩序与综合国力竞争;中国的对外政策(怎么办)。
(2)运用民族宗教的有关知识分析我国的民族关系,认识我国民族原则、民族政策和宗教政策的正确性。
(3)运用国际关系及我国的对外政策分析我国的外交政策和活动,重点联系朝核问题,中日、中美关系等。
(4)结合联合国和国际关系的有关知识分析安理会改革、国际反恐。
15.解决直线与圆的关系问题时,要充分发挥圆的平面几何性质的作用(如半径、半弦长、弦心距构成直角三角形,切线长定理、割线定理、弦切角定理等等)!
14、圆的切线与弦长:
(1)切线:①过圆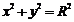 上一点
上一点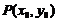 圆的切线方程是:
圆的切线方程是: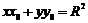 ,过圆
,过圆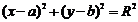 上一点
上一点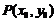 圆的切线方程是:
圆的切线方程是: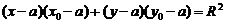 ,一般地,如何求圆的切线方程?(抓住圆心到直线的距离等于半径);②从圆外一点引圆的切线一定有两条,可先设切线方程,再根据相切的条件,运用几何方法(抓住圆心到直线的距离等于半径)来求;③过两切点的直线(即“切点弦”)方程的求法:先求出以已知圆的圆心和这点为直径端点的圆,该圆与已知圆的公共弦就是过两切点的直线方程;③切线长:过圆
,一般地,如何求圆的切线方程?(抓住圆心到直线的距离等于半径);②从圆外一点引圆的切线一定有两条,可先设切线方程,再根据相切的条件,运用几何方法(抓住圆心到直线的距离等于半径)来求;③过两切点的直线(即“切点弦”)方程的求法:先求出以已知圆的圆心和这点为直径端点的圆,该圆与已知圆的公共弦就是过两切点的直线方程;③切线长:过圆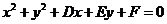 (
(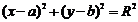 )外一点
)外一点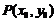 所引圆的切线的长为
所引圆的切线的长为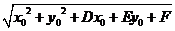 (
(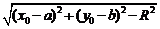 );如设A为圆
);如设A为圆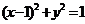 上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为__________(答:
上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为__________(答: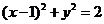 );
);
(2)弦长问题:①圆的弦长的计算:常用弦心距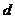 ,弦长一半
,弦长一半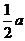 及圆的半径
及圆的半径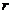 所构成的直角三角形来解:
所构成的直角三角形来解: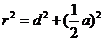 ;②过两圆
;②过两圆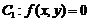 、
、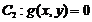 交点的圆(公共弦)系为
交点的圆(公共弦)系为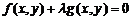 ,当
,当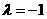 时,方程
时,方程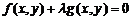 为两圆公共弦所在直线方程.。
为两圆公共弦所在直线方程.。
13、圆与圆的位置关系(用两圆的圆心距与半径之间的关系判断):已知两圆的圆心分别为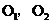 ,半径分别为
,半径分别为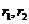 ,则(1)当
,则(1)当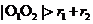 时,两圆外离;(2)当
时,两圆外离;(2)当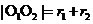 时,两圆外切;(3)当
时,两圆外切;(3)当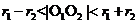 时,两圆相交;(4)当
时,两圆相交;(4)当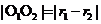 时,两圆内切;(5)当
时,两圆内切;(5)当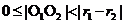 时,两圆内含。如双曲线
时,两圆内含。如双曲线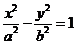 的左焦点为F1,顶点为A1、A2,P是双曲线右支上任意一点,则分别以线段PF1、A1A2为直径的两圆位置关系为 (答:内切)
的左焦点为F1,顶点为A1、A2,P是双曲线右支上任意一点,则分别以线段PF1、A1A2为直径的两圆位置关系为 (答:内切)
12、直线与圆的位置关系:直线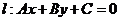 和圆
和圆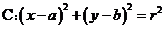
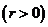 有相交、相离、相切。可从代数和几何两个方面来判断:(1)代数方法(判断直线与圆方程联立所得方程组的解的情况):
有相交、相离、相切。可从代数和几何两个方面来判断:(1)代数方法(判断直线与圆方程联立所得方程组的解的情况):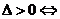 相交;
相交;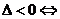 相离;
相离;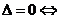 相切;(2)几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为
相切;(2)几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为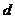 ,则
,则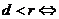 相交;
相交;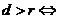 相离;
相离;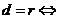 相切。提醒:判断直线与圆的位置关系一般用几何方法较简捷。如(1)圆
相切。提醒:判断直线与圆的位置关系一般用几何方法较简捷。如(1)圆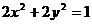 与直线
与直线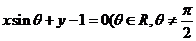
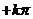 ,
,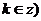 的位置关系为____(答:相离);(2)若直线
的位置关系为____(答:相离);(2)若直线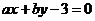 与圆
与圆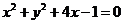 切于点
切于点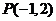 ,则
,则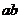 的值____(答:2);(3)直线
的值____(答:2);(3)直线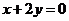 被曲线
被曲线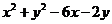
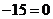 所截得的弦长等于 (答:
所截得的弦长等于 (答: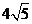 );(4)一束光线从点A(-1,1)出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 (答:4);(5)已知
);(4)一束光线从点A(-1,1)出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 (答:4);(5)已知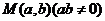 是圆
是圆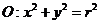 内一点,现有以
内一点,现有以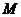 为中点的弦所在直线
为中点的弦所在直线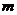 和直线
和直线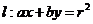 ,则A.
,则A.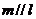 ,且
,且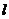 与圆相交 B.
与圆相交 B.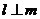 ,且
,且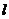 与圆相交 C.
与圆相交 C.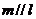 ,且
,且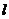 与圆相离 D.
与圆相离 D.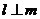 ,且
,且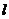 与圆相离(答:C);(6)已知圆C:
与圆相离(答:C);(6)已知圆C: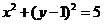 ,直线L:
,直线L: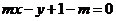 。①求证:对
。①求证:对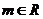 ,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若
,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若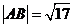 ,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程. (答:②
,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程. (答:②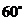 或
或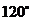 ③最长:
③最长: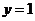 ,最短:
,最短: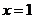 )
)
11、点与圆的位置关系:已知点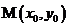 及圆
及圆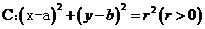 ,(1)点M在圆C外
,(1)点M在圆C外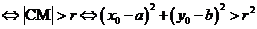 ;(2)点M在圆C内
;(2)点M在圆C内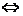
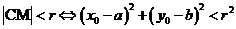 ;(3)点M在圆C上
;(3)点M在圆C上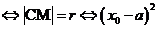
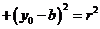 。如点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是______(答:
。如点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是______(答: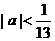 )
)
10、圆的方程:
⑴圆的标准方程: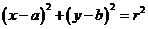 。
。
⑵圆的一般方程: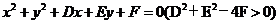 ,特别提醒:只有当
,特别提醒:只有当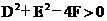 时,方程
时,方程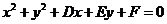 才表示圆心为
才表示圆心为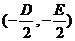 ,半径为
,半径为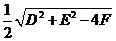 的圆(二元二次方程
的圆(二元二次方程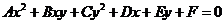 表示圆的充要条件是什么? (
表示圆的充要条件是什么? (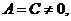 且
且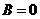 且
且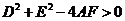 ));
));
⑶圆的参数方程: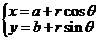 (
(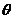 为参数),其中圆心为
为参数),其中圆心为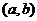 ,半径为
,半径为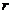 。圆的参数方程的主要应用是三角换元:
。圆的参数方程的主要应用是三角换元: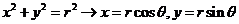 ;
;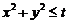
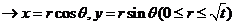 。
。
⑷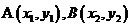 为直径端点的圆方程
为直径端点的圆方程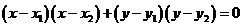
如(1)圆C与圆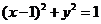 关于直线
关于直线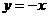 对称,则圆C的方程为____________(答:
对称,则圆C的方程为____________(答: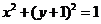 );(2)圆心在直线
);(2)圆心在直线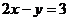 上,且与两坐标轴均相切的圆的标准方程是__________(答:
上,且与两坐标轴均相切的圆的标准方程是__________(答: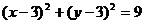 或
或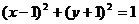 );(3)已知
);(3)已知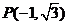 是圆
是圆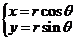 (
(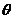 为参数,
为参数,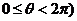 上的点,则圆的普通方程为________,P点对应的
上的点,则圆的普通方程为________,P点对应的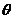 值为_______,过P点的圆的切线方程是___________(答:
值为_______,过P点的圆的切线方程是___________(答: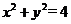 ;
;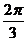 ;
;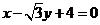 );(4)如果直线
);(4)如果直线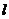 将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么
将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么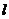 的斜率的取值范围是____(答:[0,2]);(5)方程x2+y2-x+y+k=0表示一个圆,则实数k的取值范围为____(答:
的斜率的取值范围是____(答:[0,2]);(5)方程x2+y2-x+y+k=0表示一个圆,则实数k的取值范围为____(答: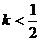 );(6)若
);(6)若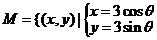 (
(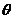 为参数,
为参数,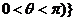 ,
,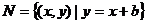 ,若
,若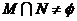 ,则b的取值范围是_________(答:
,则b的取值范围是_________(答: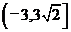 )
)
9、简单的线性规划:
(1)二元一次不等式表示的平面区域:①法一:先把二元一次不等式改写成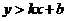 或
或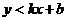 的形式,前者表示直线的上方区域,后者表示直线的下方区域;法二:用特殊点判断;②无等号时用虚线表示不包含直线
的形式,前者表示直线的上方区域,后者表示直线的下方区域;法二:用特殊点判断;②无等号时用虚线表示不包含直线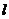 ,有等号时用实线表示包含直线
,有等号时用实线表示包含直线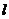 ;③设点
;③设点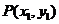 ,
,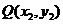 ,若
,若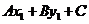 与
与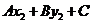 同号,则P,Q在直线
同号,则P,Q在直线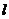 的同侧,异号则在直线
的同侧,异号则在直线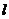 的异侧。如已知点A(-2,4),B(4,2),且直线
的异侧。如已知点A(-2,4),B(4,2),且直线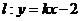 与线段AB恒相交,则
与线段AB恒相交,则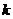 的取值范围是__________(答:
的取值范围是__________(答: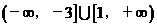 )
)
(2)线性规划问题中的有关概念:
①满足关于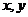 的一次不等式或一次方程的条件叫线性约束条件。
的一次不等式或一次方程的条件叫线性约束条件。
②关于变量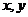 的解析式叫目标函数,关于变量
的解析式叫目标函数,关于变量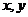 一次式的目标函数叫线性目标函数;
一次式的目标函数叫线性目标函数;
③求目标函数在线性约束条件下的最大值或最小值的问题,称为线性规划问题;
④满足线性约束条件的解(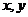 )叫可行解,由所有可行解组成的集合叫做可行域;
)叫可行解,由所有可行解组成的集合叫做可行域;
⑤使目标函数取得最大值或最小值的可行解叫做最优解;
(3)求解线性规划问题的步骤是什么?①根据实际问题的约束条件列出不等式;②作出可行域,写出目标函数;③确定目标函数的最优位置,从而获得最优解。如(1)线性目标函数z=2x-y在线性约束条件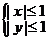 下,取最小值的最优解是____(答:(-1,1));(2)点(-2,
下,取最小值的最优解是____(答:(-1,1));(2)点(-2,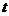 )在直线2x-3y+6=0的上方,则
)在直线2x-3y+6=0的上方,则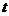 的取值范围是_________(答:
的取值范围是_________(答: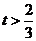 );(3)不等式
);(3)不等式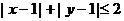 表示的平面区域的面积是_________(答:8);(4)如果实数
表示的平面区域的面积是_________(答:8);(4)如果实数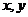 满足
满足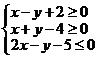 ,则
,则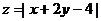 的最大值_________(答:21)
的最大值_________(答:21)
(4)在求解线性规划问题时要注意:①将目标函数改成斜截式方程;②寻找最优解时注意作图规范。
8、对称(中心对称和轴对称)问题--代入法:如(1)已知点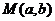 与点
与点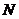 关于
关于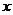 轴对称,点P与点N关于
轴对称,点P与点N关于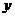 轴对称,点Q与点P关于直线
轴对称,点Q与点P关于直线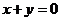 对称,则点Q的坐标为_______(答:
对称,则点Q的坐标为_______(答: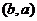 );(2)已知直线
);(2)已知直线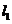 与
与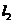 的夹角平分线为
的夹角平分线为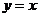 ,若
,若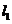 的方程为
的方程为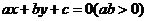 ,那么
,那么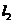 的方程是___________(答:
的方程是___________(答: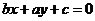 );(3)点A(4,5)关于直线
);(3)点A(4,5)关于直线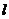 的对称点为B(-2,7),则
的对称点为B(-2,7),则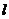 的方程是_________(答:
的方程是_________(答: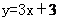 );(4)已知一束光线通过点A(-3,5),经直线
);(4)已知一束光线通过点A(-3,5),经直线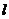 :3x-4y+4=0反射。如果反射光线通过点B(2,15),则反射光线所在直线的方程是_________(答:
:3x-4y+4=0反射。如果反射光线通过点B(2,15),则反射光线所在直线的方程是_________(答: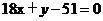 );(5)已知ΔABC顶点A(3,-1),AB边上的中线所在直线的方程为6x+10y-59=0,∠B的平分线所在的方程为x-4y+10=0,求BC边所在的直线方程(答:
);(5)已知ΔABC顶点A(3,-1),AB边上的中线所在直线的方程为6x+10y-59=0,∠B的平分线所在的方程为x-4y+10=0,求BC边所在的直线方程(答: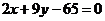 );(6)直线2x―y―4=0上有一点P,它与两定点A(4,-1)、B(3,4)的距离之差最大,则P的坐标是______(答:(5,6));(7)已知
);(6)直线2x―y―4=0上有一点P,它与两定点A(4,-1)、B(3,4)的距离之差最大,则P的坐标是______(答:(5,6));(7)已知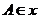 轴,
轴,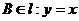 ,C(2,1),
,C(2,1),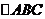 周长的最小值为______(答:
周长的最小值为______(答: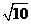 )。提醒:在解几中遇到角平分线、光线反射等条件常利用对称求解。
)。提醒:在解几中遇到角平分线、光线反射等条件常利用对称求解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com