
26.(2009湖北卷文)已知{an}是一个公差大于0的等差数列,
且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an== ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn 

解(1)解:设等差数列 的公差为d,则依题设d>0
的公差为d,则依题设d>0 

由a2+a7=16.得 ①
①
由 得
得 ②
②
由①得 将其代入②得
将其代入②得 。即
。即



(2)令
两式 相减得
相减得
于是
= -4=
-4=
25. (2009陕西卷文)已知数列 满足,
满足,
 .
.
 令
令 ,证明:
,证明: 是等比数列;
是等比数列;
(Ⅱ)求 的通项公式。
的通项公式。
(1)证
当 时,
时,
所以 是以1为首项,
是以1为首项, 为公比的等比数列。
为公比的等比数列。
(2)解由(1)知
当 时,
时,




当 时,
时, 。
。
所以 。
。
24. (2009辽宁卷文)等比数列{ }的前n 项和为
}的前n 项和为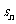 ,已知
,已知 ,
, ,
, 成等差数列
成等差数列
(1)求{ }的公比q;
}的公比q;
(2)求 -
- =3,求
=3,求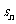


解:(Ⅰ)依题意有 


由于  ,故
,故
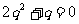
又 ,从而
,从而 5分
5分
(Ⅱ)由已知可得
故
从而 10分
10分
23. (2009全国卷Ⅱ理)设数列 的前
的前 项和为
项和为 已知
已知

(I)设 ,证明数列
,证明数列 是等比数列
是等比数列
(II)求数列 的通项公式。
的通项公式。
解:(I)由 及
及 ,有
,有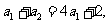

由 ,...①
则当
,...①
则当 时,有
时,有 .....②
.....②
②-①得
又 ,
,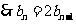
 是首项
是首项 ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得 ,
,
 数列
数列 是首项为
是首项为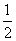 ,公差为
,公差为 的等比数列.
的等比数列.

 ,
,
评析:第(I)问思路明确,只需利用已知条件寻找 .
.
第(II)问中由(I)易得 ,这个递推式明显是一个构造新数列的模型:
,这个递推式明显是一个构造新数列的模型: ,主要的处理手段是两边除以
,主要的处理手段是两边除以 .
.
总体来说,09年高考理科数学全国I、Ⅱ这两套试题都将数列题前置,主要考查构造新数列(全国I还考查了利用错位相减法求前n项和的方法),一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式。具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用。也可看出命题人在有意识降低难度和求变的良苦用心。
22. (2009天津卷文)已知等差数列 的公差d不为0,设
的公差d不为0,设

(Ⅰ)若 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若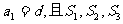 成等比数列,求q的值。
成等比数列,求q的值。
(Ⅲ)若
(1)解:由题设,
代入解得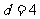 ,所以
,所以

(2)解:当 成等比数列,所以
成等比数列,所以 ,即
,即 ,注意到
,注意到 ,整理得
,整理得
(3)证明:由题设,可得 ,则
,则
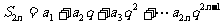 ①
①
 ②
②
①-②得,

①+②得,
 ③
③
③式两边同乘以 q,得
所以
(3)证明:
=
因为 ,所以
,所以

若 ,取i=n,
,取i=n,
若 ,取i满足
,取i满足 ,且
,且 ,
,
由(1)(2)及题设知, ,且
,且



①
当 时,
时, ,由
,由 ,
,
即 ,
,

所以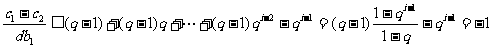
因此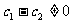
②
当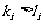 时,同理可得
时,同理可得 因此
因此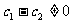


综上,
[考点定位]本小题主要考查了等差数列的通项公式,等比数列通项公式与前n项和等基本知识,考查运算能力和推理论证能力和综合分析解决问题的能力。
21.(2009江西卷文)数列 的通项
的通项 ,其前n项和为
,其前n项和为 .
.
(1) 求 ;
;
(2)  求数列{
求数列{ }的前n项和
}的前n项和 .
.
解: (1) 由于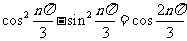 ,故
,故

 ,
,


故  (
( )
)
(2) 
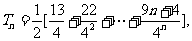

两式相减得

故 
20.(2009安徽卷文)已知数列{ } 的前n项和
} 的前n项和 ,数列{
,数列{ }的前n项和
}的前n项和
(Ⅰ)求数列{ }与{
}与{ }的通项公式;
}的通项公式;
(Ⅱ)设 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时, <
<


[思路]由 可求出
可求出 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出 后,进而得到
后,进而得到 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
[解析](1)由于
当 时,
时, 

又当 时
时

 数列
数列 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为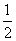



(2)由(1)知

由 即
即 即
即
又 时
时 成立,即
成立,即 由于
由于 恒成立.
恒成立. 

因此,当且仅当 时,
时, 
19.(2009全国卷Ⅱ文)已知等差数列{ }中,
}中,
 求{
求{ }前n项和
}前n项和 .
. 

解析:本题考查等差数列的基本性质及求和公式运用能力,利用方程的思想可求解。
解:设 的公差为
的公差为 ,则
,则 


即
解得
因此
18.(2009山东卷文)等比数列{ }的前n项和为
}的前n项和为 ,
已知对任意的
,
已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上. 

(1)求r的值;
(11)当b=2时,记  求数列
求数列 的前
的前 项和
项和
解:因为对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.所以得
均为常数)的图像上.所以得 ,
,
当 时,
时, ,
, 

当 时,
时, ,
,
又因为{ }为等比数列, 所以
}为等比数列, 所以 , 公比为
, 公比为 , 所以
, 所以
(2)当b=2时,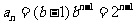 ,
, 
则



相减,得


所以
[命题立意]:本题主要考查了等比数列的定义,通项公式,以及已知 求
求 的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前
的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前 项和
项和 .
.
17.(2009北京文)设数列 的通项公式为
的通项公式为 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值.
成立的所有n中的最小值.
(Ⅰ)若 ,求
,求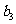 ;
;
(Ⅱ)若 ,求数列
,求数列 的前2m项和公式;
的前2m项和公式;
(Ⅲ)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
[解析]本题主要考查数列的概念、数列的基本性质,考查运算能力、推理论证能力、
分类讨论等数学思想方法.本题是数列与不等式综合的较难层次题.
解(Ⅰ)由题意,得 ,解
,解 ,得
,得 .
. 

∴ 成立的所有n中的最小整数为7,即
成立的所有n中的最小整数为7,即 .
.
(Ⅱ)由题意,得 ,
,
对于正整数,由 ,得
,得 .
.
根据 的定义可知
的定义可知
当 时,
时, ;当
;当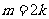 时,
时, .
.
∴

 .
.
(Ⅲ)假设存在p和q满足条件,由不等式 及
及 得
得 .
.
∵ ,根据
,根据 的定义可知,对于任意的正整数m 都有
的定义可知,对于任意的正整数m 都有
 ,即
,即 对任意的正整数m都成立.
对任意的正整数m都成立.
当 (或
(或 )时,得
)时,得 (或
(或 ),
),
这与上述结论矛盾!
当 ,即
,即 时,得
时,得 ,解得
,解得 .
.
∴ 存在p和q,使得 ;
;
p和q的取值范围分别是 ,
, ..
..
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com