
9.(江西省临川一中2008届高三模拟试题)等差数列有如下性质,若数列 是等差数列,则当
是等差数列,则当 也是等差数列;类比上述性质,相应地
也是等差数列;类比上述性质,相应地 是正项等比数列,当数列
是正项等比数列,当数列 时,数列
时,数列 也是等比数列。
也是等比数列。
答案 
8.(山东省潍坊市2008年高三教学质量检测) 设等差数列{an}的前n项和为Sn,若 ,则S19=______________.
,则S19=______________.
答案 190
7.(2007-2008学年湖北省黄州西湖中学二月月考试卷) 为等差数列
为等差数列 的前n项和,若
的前n项和,若 ,则
,则 =
.
=
.
答案 4
解析: 由 ,即
,即
 ,得
,得 .
.
 ,
, .故
.故 =4.
=4.
6.(江苏省省阜中2008届高三第三次调研考试数学) 在等差数列 中,
中, 若它的前n项和
若它的前n项和 有最大值,则使
有最大值,则使 取得最小正数的
取得最小正数的 .
.
答案19
5.. (上海市嘉定一中2007学年第一学期高三年级测试(二)) 等差数列{an}共有2n项,其中奇数项的和为90,偶数项的和为72,且 ,则该数列的公差为 (
)
,则该数列的公差为 (
)
A.3 B-3 C.-2 D.-1
答案 B
4.
(2008年天津市十二区县重点学校高三毕业班联考(一))正项等比数列 满足
满足 ,
, ,
, ,则数列
,则数列 的前10项和是
的前10项和是
A.65 B.-65 C.25 D. -25
答案 D
3.(湖南省2008届十二校联考第一次考试)在等比数列 ( )
( )
A. B.
B. C.
C. D.
D.
答案 D
2.(山东省潍坊市2007-2008学年度高三第一学期期末考试) 各项都是正数的等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则 的值为( )
的值为( )
A. B.
B. C.
C.  D.
D. 或
或
答案 C
1.( 上海市部分重点中学高三第一次联考)
等差数列 的前n项和
的前n项和 当首项
当首项 和公差d变化时,若
和公差d变化时,若 是一个定值,则下列各数中为定值的是―――――――――( )
是一个定值,则下列各数中为定值的是―――――――――( )
A、 B.
B. S
S C、
C、 D、
D、
答案 B
3.(2009上海八校联考)已知点列
 顺次为直线
顺次为直线 上的点,点列
上的点,点列
 顺次为
顺次为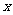 轴上的点,其中
轴上的点,其中
 ,对任意的
,对任意的 ,点
,点 、
、 、
、 构成以
构成以 为顶点的等腰三角形。
为顶点的等腰三角形。
(1)证明:数列 是等差数列;
是等差数列;
(2)求证:对任意的 ,
, 是常数,并求数列
是常数,并求数列 的通项公式;
的通项公式;
(3)对上述等腰三角形 添加适当条件,提出一个问题,并做出解答。
添加适当条件,提出一个问题,并做出解答。
(根据所提问题及解答的完整程度,分档次给分)
解: (1)依题意有 ,于是
,于是 .
.
所以数列 是等差数列.
是等差数列.
 .4分
.4分
(2)由题意得 ,即
,即 , (
, ( )
①
)
①
所以又有 .
②
.
②
由② ①得:
①得: , 所以
, 所以 是常数.
是常数.  6分
6分
由 都是等差数列.
都是等差数列.
 ,那么得
,那么得  ,
,
 . (
. (


 8分
8分
故
 10分
10分
(3) 提出问题①:若等腰三角形 中,是否有直角三角形,若有,求出实数
中,是否有直角三角形,若有,求出实数
提出问题②:若等腰三角形 中,是否有正三角形,若有,求出实数
中,是否有正三角形,若有,求出实数
解:问题①  11分
11分
当 为奇数时,
为奇数时, ,所以
,所以
当 为偶数时,
为偶数时, 所以
所以
作 轴,垂足为
轴,垂足为 则
则 ,要使等腰三角形
,要使等腰三角形 为直角三角形,必须且只须:
为直角三角形,必须且只须: .
.
 13分
13分
当 为奇数时,有
为奇数时,有 ,即
,即 ①
①
 , 当
, 当 ,
,  不合题意.
不合题意. 15分
15分
当 为偶数时,有
为偶数时,有 ,
, ,同理可求得
,同理可求得 
当 时,
时, 不合题意.
不合题意.  17分
17分
综上所述,使等腰三角形 中,有直角三角形,
中,有直角三角形, 的值为
的值为 或
或 或
或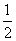 .
.
 18分
18分
解:问题②  11分
11分
当 为奇数时,
为奇数时, ,所以
,所以
当 为偶数时,
为偶数时, 所以
所以
作 轴,垂足为
轴,垂足为 则
则 ,要使等腰三角形
,要使等腰三角形 为正三角形,必须且只须:
为正三角形,必须且只须: .
.
 13分
13分
当 为奇数时,有
为奇数时,有 ,即
,即 ①
①
 , 当
, 当 时,.
时,.  不合题意.
不合题意.  15分
15分
当 为偶数时,有
为偶数时,有 ,
, ,同理可求得
,同理可求得  .
.
 ;
; ;当
;当 时,
时, 不合题意.
不合题意. 17分
17分
综上所述,使等腰三角形 中,有正三角形,
中,有正三角形, 的值为
的值为
 ;
;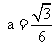 ;
; ;
;
 18分
18分
2007--2008年联考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com