
8.设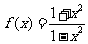 ,求证:
,求证:
(1)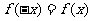 ; (2)
; (2)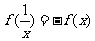 .
.
7.解:(1)因为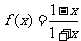 ,
,
所以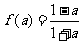 ,得
,得 ,
,
即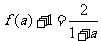 ;
;
(2)因为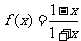 ,
,
所以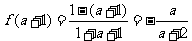 ,
,
即 .
.
7.已知函数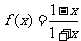 ,求:
,求:
(1) ; (2)
; (2) .
.
6.解:(1)要使原式有意义,则 ,即
,即 ,
,
得函数的定义域为 ;
;
(2)要使原式有意义,则 ,即
,即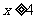 ,且
,且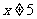 ,
,
得函数的定义域为 .
.
6.求下列函数的定义域:
(1)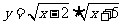 ;
;
(2) .
.
5.解:集合 ,即
,即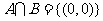 ;
;
集合 ,即
,即 ;
;
集合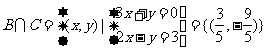 ;
;
则 .
.
5.已知集合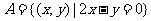 ,
,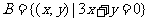 ,
,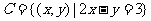 ,求
,求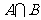 ,
,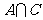 ,
, .
.
4.解:显然集合 ,对于集合
,对于集合 ,
,
当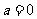 时,集合
时,集合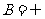 ,满足
,满足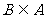 ,即
,即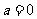 ;
;
当 时,集合
时,集合 ,而
,而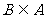 ,则
,则 ,或
,或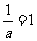 ,
,
得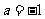 ,或
,或 ,
,
综上得:实数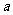 的值为
的值为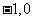 ,或
,或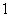 .
.
4.已知集合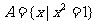 ,
, .若
.若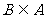 ,求实数
,求实数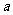 的值.
的值.
3.解:集合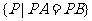 表示的点组成线段
表示的点组成线段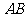 的垂直平分线,
的垂直平分线,
集合 表示的点组成线段
表示的点组成线段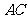 的垂直平分线,
的垂直平分线,
得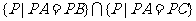 的点是线段
的点是线段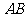 的垂直平分线与线段
的垂直平分线与线段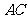 的
的
垂直平分线的交点,即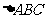 的外心.
的外心.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com