21.(10分)如图，平行四边形ABCD中，AB⊥AC,AB=2,BC=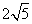，对角线AC、BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC、AD于点F、E.

(1)证明：当旋转角度为90°时，四边形ABFE是平行四边形．

(2)试说明在旋转过程中，线段AF与EC总是保持相等．

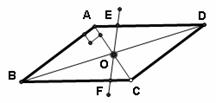(3)在旋转过程中四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由，并求出此时AC绕点O顺时针旋转的度数．

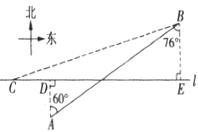
20.(9分)如图，在航线L的两侧分别有观测点A和B，点A到航线L的的距离为2千米，点B位于点A的北偏东60°方向且与A相距10千米处，现有一艘轮船从位于点B南偏西

76°方向的C处，正沿着该航线自西向东航行，5min后轮船行至点A的正北方向的D处

(1)求观测点B到航线L的距离．

(2)求轮船航行的速度．(结果精确到0.1千米/时)

(参考数据：)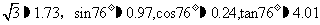

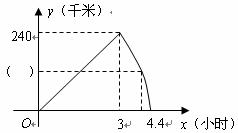
19.(9分)甲、乙两车同时从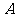地出发，以各自的速度匀速向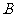地行驶．甲车先到达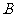地，停留1小时后按原路以另一速度匀速返回，直到两车相遇．乙车的速度为每小时120千米．下图是两车之间的距离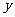(千米)与乙车行驶时间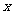(小时)之间的函数图象．

(1)请将图中的(　 )内填上正确的值，并直接写出甲车从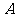到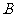的行驶速度；

(2)求从甲车返回到与乙车相遇过程中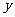与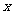之间的函数关系式，并写出自变量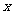的取值范围．

(3)求出甲车返回时行驶速度及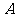、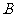两地的距离．

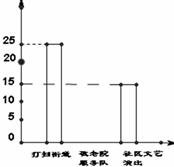
18.(9分)某中学组织全体学生参加“校园服务进社区”活动，九年级三班张明同学统计了某天本班同学打扫街道、参加敬老院服务队和社区文艺演出的人数并绘制如下的扇形统计图和不完整的条形统计图，请根据张明同学的统计图，解答下面问题：

(1)九年级三班有多少名学生？

(2)补全条形统计图．

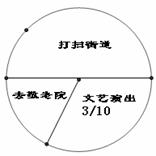(3)若九年级有800名学生，估计该年级去敬老院服务队的人数？

17.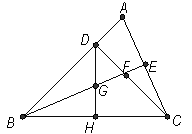(9分)已知：如图所示△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连接DH与BE相交于点G.(1)求证：BF=AC；．

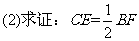(3)CE与BG的大小关系如何？试证明你的结论．

16.(8分)先化简，再求值：

．

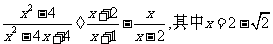15.已知M(a,b)是平面直角坐标系中的点，其中a是从1、2、3 三个数中任取的一个数，b是从1、2、3、4四个数中任取的一个数，定义“点M(a，b)在直线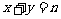上”为事件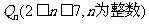,当Q_n的概率最大时，n的所有可能值为　　　　　　 ．

14.如图所示，Rt△ABC中，∠ACB=90°∠A﹤∠B,以AB边上的中线CM为折痕，将△ACM折叠，使点A落在点D处，如果CD恰好与AB垂直，则tanA=　　　　　　 ．

13.已知在Rt△ABC中，∠C=90°，AC=3,BC=4.⊙O是Rt△ABC的外接圆，现小明同学随机的在⊙O及其内部区域做投针实验，则针投到Rt△ABC区域的概率是：　　　　　　　　 ．

12.如图所示，点A是半圆上的一个三等分点，B是劣弧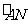的中点，点P是直径MN上的一个动点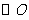，的半径为1，则AP+PB的最小值　　　 ．