
17. (本题13分)
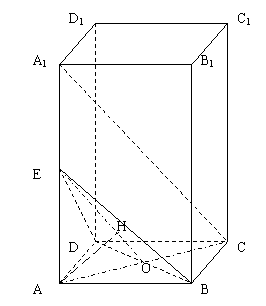 如图,在正四棱柱
如图,在正四棱柱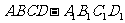 中,
中,
棱长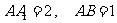 ,
,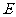 是
是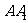 的中点。
的中点。
(Ⅰ)求证: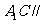 平面
平面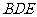
(Ⅱ)求点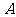 到平面
到平面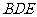 的距离
的距离
(Ⅰ)证明:连结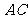 ,交
,交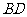 于
于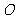 ,连结
,连结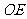 ……1分
……1分
 正四棱柱
正四棱柱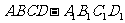 中,底面
中,底面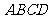 是正方形
是正方形
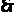 点
点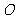 是
是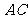 的中点 ……2分
的中点 ……2分
又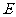 是
是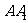 的中点
的中点 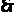
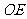 是
是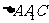 的中位线
的中位线 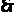
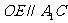 ……4分
……4分

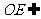 平面
平面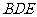 ,
,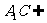 平面
平面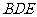 ,
,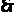
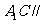 平面
平面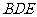 ……6分
……6分
(Ⅱ)解:过点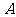 作
作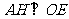 ,垂足为
,垂足为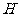 ……7分
……7分
 正四棱柱
正四棱柱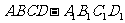 中,底面
中,底面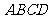 是正方形
是正方形
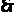
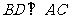 ,
,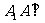 平面
平面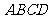 ……8分
……8分
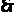
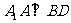 ……9分
……9分
又
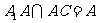
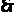
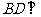 平面
平面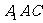
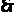
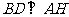 ……10分
……10分
又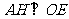 ,
,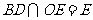
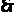
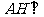 平面
平面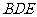 ……11分
……11分
在 中,
中,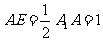 ,
,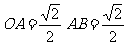 ,
,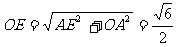
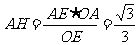 即点
即点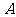 到平面
到平面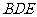 的距离是
的距离是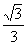 ……13分
……13分
16. (本题13分)
已知函数
(Ⅰ)求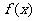 在
在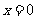 处的切线方程
处的切线方程
(Ⅱ)求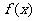 在区间
在区间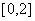 上的最大值和最小值
上的最大值和最小值
解:(Ⅰ)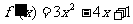 ……2分
……2分
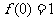 ,切点坐标
,切点坐标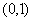 ……3分
……3分
切线斜率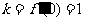 ……4分
……4分
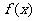 在
在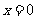 处的切线方程为
处的切线方程为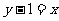 即
即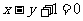 ……6分
……6分
(Ⅱ)令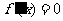 ,解得
,解得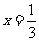 或
或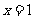 ……8分
……8分
在区间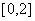 上
上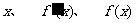 的关系如下表 ……10分
的关系如下表 ……10分
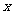 |
0 |
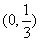 |
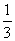 |
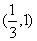 |
1 |
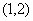 |
2 |
 |
|
+ |
0 |
- |
0 |
+ |
|
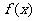 |
1 |
↗ |
极大值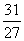 |
↘ |
极小值1 |
↗ |
3 |
因此 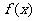 在区间
在区间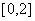 上的最大值是 3 最小值是1 ……13分
上的最大值是 3 最小值是1 ……13分
15.(本题13分)
已知向量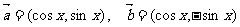
(Ⅰ)若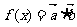 ,求
,求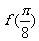
(Ⅱ)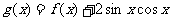 ,求
,求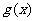 的周期和最小值
的周期和最小值
解:(Ⅰ)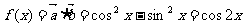 ……4分
……4分
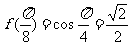 ……6分
……6分
(Ⅱ)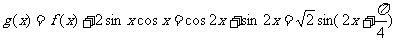 ……9分
……9分
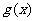 的周期
的周期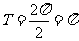 ……10分
……10分
当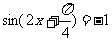 时,函数
时,函数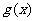 有最小值
有最小值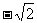 ……13分
……13分
20.(本小题满分13分)
若数列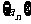
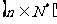 满足:(1)
满足:(1)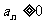 ;(2)
;(2)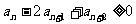 ;
;
(3)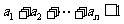 ,则称数列
,则称数列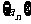 为“和谐”数列.
为“和谐”数列.
(Ⅰ)验证数列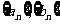 ,其中
,其中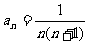 ,
,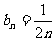 是否为“和谐”数列;
是否为“和谐”数列;
(Ⅱ)若数列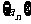 为“和谐”数列,证明:
为“和谐”数列,证明: .
.
18.(本小题满分13分)
已知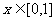 ,函数
,函数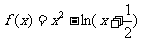 ,
, .
.
(Ⅰ)求函数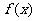 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设 若
若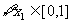 ,总存在
,总存在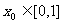 ,使得
,使得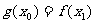 成立,求
成立,求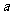 的取值范围.
的取值范围.
|
已知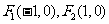 是椭圆C的两个焦点,
是椭圆C的两个焦点,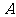 、
、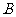 为过
为过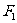 的直线与椭圆的交点,且
的直线与椭圆的交点,且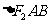 的周长为
的周长为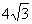 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)判断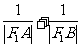 是否为定值,若是求出这个值,若不是说明理由.
是否为定值,若是求出这个值,若不是说明理由.
17.(本小题满分14分)
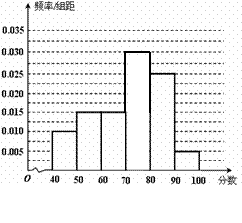 从参加高三年级期中考试的学生中随机抽出40名学生,将其数学成绩(均为整数)分成六组[40,50
从参加高三年级期中考试的学生中随机抽出40名学生,将其数学成绩(均为整数)分成六组[40,50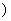 ,[50,60
,[50,60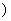 ,…[90,100]后得到如下频率分布直方图.
,…[90,100]后得到如下频率分布直方图.
(Ⅰ)同一组数据用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅱ)从上述40名学生中随机抽取2人,求这2人成绩都在[70,80 的概率;
的概率;
(Ⅲ)从上述40名学生中随机抽取2人,抽到的学生成绩在[40,60 ,记为0分,在[60,100],记为1分.用X表示抽取结束后的总记分,求X的分布列和数学期望.
,记为0分,在[60,100],记为1分.用X表示抽取结束后的总记分,求X的分布列和数学期望.
16.(本小题满分14分)
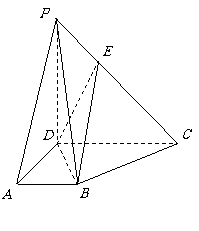 如图:
如图: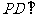 平面
平面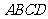 ,四边形ABCD为直角梯形,
,四边形ABCD为直角梯形,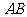 //
//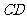 ,
,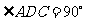 ,
,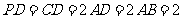 ,,
,,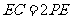 .
.
(Ⅰ) 求证: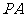 //平面
//平面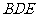 ;
;
(Ⅱ) 求证:平面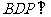 平面
平面 ;
;
(Ⅲ) 求二面角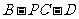 的余弦值.
的余弦值.
15.(本小题满分13分)
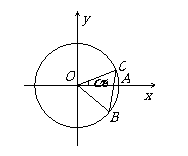 如图,圆
如图,圆 与
与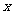 轴的正半轴的交点为
轴的正半轴的交点为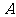 ,点
,点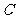 、
、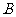 在圆
在圆 上,且点
上,且点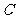 位于第一象限,点
位于第一象限,点 的坐标为
的坐标为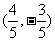 ,
,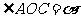 .
.
(Ⅰ)求圆 的半径及
的半径及 点的坐标;
点的坐标;
(Ⅱ)若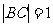 ,求
,求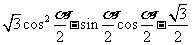 的值.
的值.
14.用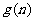 表示自然数
表示自然数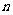 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
的所有因数中最大的那个奇数,例如:9的因数有1,3,9,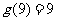 ,10的因数有1,2,5,10,
,10的因数有1,2,5,10,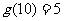 ,那么
,那么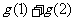
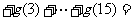 ;
;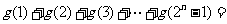 .
.
13.函数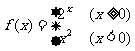 ,若
,若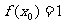 ,则
,则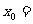 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com