
7.
已知曲线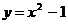 上的两点A(2,3),
上的两点A(2,3), ,当
,当 时,割线AB的斜率是__________,当
时,割线AB的斜率是__________,当 时,割线AB的斜率是__________,曲线在点A处的切线方程是________________________。
时,割线AB的斜率是__________,曲线在点A处的切线方程是________________________。
6.设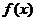 为可导函数,且满足条件
为可导函数,且满足条件 ,则曲线
,则曲线 在点
在点
(1,1)处的切线的斜率为( )
A 2 B -1 C 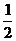 D -2
D -2
5.若 ,则
,则 =( )
=( )
A -3 B -6 C -9 D -12
4.已知曲线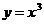 上过点(2,8)的切线方程为
上过点(2,8)的切线方程为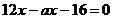 ,则实数
,则实数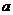 的值为( )
的值为( )
A -1 B 1 C -2 D 2
3.函数 在
在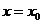 处的导数
处的导数 的几何意义是( )
的几何意义是( )
A 在点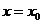 处的函数值
处的函数值
B 在点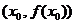 处的切线与
处的切线与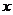 轴所夹锐角的正切值
轴所夹锐角的正切值
C 曲线 在点
在点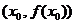 处的切线的斜率
处的切线的斜率
D 点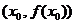 与点(0,0)连线的斜率
与点(0,0)连线的斜率
例1.
如图(见课本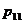 .5),试描述函数
.5),试描述函数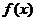 在
在 附近的变化情况。
附近的变化情况。
变式 根据下列条件,分别画出函数图像在这点附近的大致形状:
(1) ;(2)
;(2)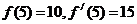 ;(3)
;(3)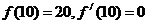 。
。
例2.如图(见课本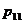 .6)已知函数
.6)已知函数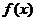 的图像,试画出其导函数
的图像,试画出其导函数 图像的大致形状。
图像的大致形状。
变式:根据下面的文字叙述,画出相应的路程关于时间的函数图像的大致形状。
(1)汽车在笔直的公路上匀速行驶;
(2)汽车在笔直的公路上不断加速行驶;
(3)汽车在笔直的公路上不断减速行驶;
例3.已知曲线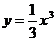 上的一点
上的一点 ,求(1)点P处切线的斜率;(2)点P处的切线方程。
,求(1)点P处切线的斜率;(2)点P处的切线方程。
变式:已知曲线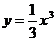 ,求与直线
,求与直线 垂直,并与该曲线相切的直线方程。
垂直,并与该曲线相切的直线方程。
作业:1.曲线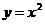 在
在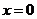 处的( )
处的( )
A 切线斜率为1 B 切线方程为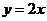 C 没有切线 D 切线方程为
C 没有切线 D 切线方程为
2.已知曲线 上的一点A(2,8),则点A处的切线斜率为( )
上的一点A(2,8),则点A处的切线斜率为( )
A 4 B 16 C 8 D 2
3.当函数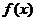 在
在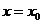 处的导数
处的导数 ,函数在
,函数在 附近的图像自左而右是__________的,并且
附近的图像自左而右是__________的,并且 的值越大,图像上升的就越________;当函数
的值越大,图像上升的就越________;当函数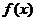 在
在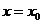 处的导数
处的导数 ,函数在
,函数在 附近的图像自左而右是__________的,并且
附近的图像自左而右是__________的,并且 的值越小,图像下降的就越________;
的值越小,图像下降的就越________;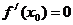 ,函数在
,函数在 附近几乎______________________。
附近几乎______________________。
2.函数的平均变化率的几何意义是___________________________;函数的导数的几何意义是______________________________。
1.对于函数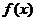 的曲线上的定点
的曲线上的定点 和动点
和动点 ,直线
,直线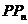 称为这条函数曲线上过
称为这条函数曲线上过 点的一条__________;其斜率
点的一条__________;其斜率 =_________________;当
=_________________;当 时,直线
时,直线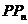 就无限趋近于一个确定的位置,这个确定位置的直线PT称为过P点的__________;其斜率
就无限趋近于一个确定的位置,这个确定位置的直线PT称为过P点的__________;其斜率 =________________=___________________(其中
=________________=___________________(其中 ),切线方程为________________________________;过函数曲线上任意一点的切线最多有__________条,而割线可以作_______条。
),切线方程为________________________________;过函数曲线上任意一点的切线最多有__________条,而割线可以作_______条。
21、一定条件下,氨气与一氧化氮发生反应4NH3+6NO=5N2+6H2O。该反应中化合价降低的元素是 ( )
A.NH3中的N B.NO中的O C.NO中的N D.NH3中的H
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com