
9.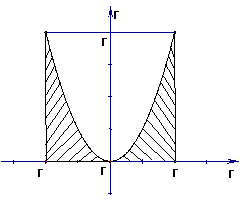 如图,设
如图,设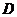 是图中边长为
是图中边长为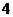 的正方形区域,
的正方形区域,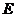 是
是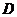 内函数
内函数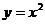 图象下方的点构成的区域.向
图象下方的点构成的区域.向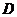 中随机投一点,则该点落入
中随机投一点,则该点落入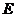 中的概率为
中的概率为
A.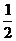
B.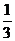
C.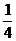
D. 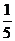
8.函数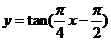 的部分图象如图所示,则
的部分图象如图所示,则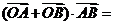
 A.
A.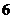
B.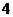
C.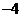
D.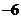
7.若直线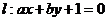 始终平分圆
始终平分圆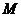 :
: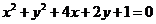 的周长,则
的周长,则
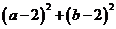 的最小值为
的最小值为
A.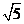 B.
B.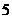 C.
C.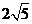 D.
D.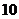
6.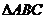 中,
中,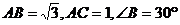 ,则
,则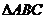 的面积等于
的面积等于
A.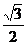 B.
B.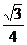 C.
C.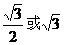 D.
D.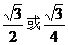
5. 在图所示的斜截圆柱中,已知圆柱底面的直径为
在图所示的斜截圆柱中,已知圆柱底面的直径为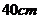 ,母线长最短
,母线长最短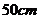 ,最长
,最长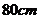 ,则斜截圆柱的侧面面积
,则斜截圆柱的侧面面积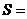
A.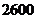
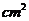
B.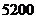
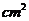
C.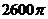
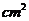
D.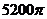
4.为了得到函数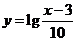 的图像,只需把函数
的图像,只需把函数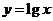 的图像上所有的点
的图像上所有的点
A.向左平移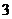 个单位长度,再向上平移
个单位长度,再向上平移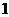 个单位长度
个单位长度
B.向右平移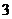 个单位长度,再向上平移
个单位长度,再向上平移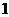 个单位长度
个单位长度
C.向左平移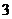 个单位长度,再向下平移
个单位长度,再向下平移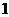 个单位长度
个单位长度
D.向右平移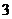 个单位长度,再向下平移
个单位长度,再向下平移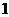 个单位长度
个单位长度
3.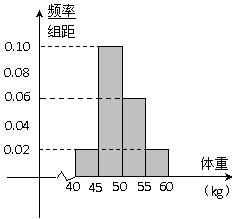 某校为了了解高三学生的身体状况,抽取了
某校为了了解高三学生的身体状况,抽取了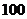 名女生的体重.将所得的数据整理后,画出了如图的频率分布直方图,则所抽取
名女生的体重.将所得的数据整理后,画出了如图的频率分布直方图,则所抽取
的女生中体重在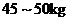 的人数是
的人数是
A.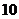
B.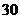
C.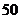
D.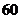
2.下列命题中的真命题是
A.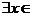
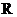 ,使得
,使得  B.
B.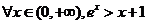
C.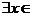
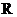 ,使得
,使得 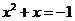 D.
D.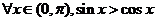
1.集合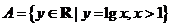 ,
,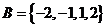 ,则下列结论正确的是
,则下列结论正确的是
A.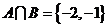 B.
B.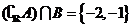
C. 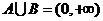 D.
D. 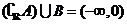
4、注意区分“求曲线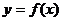 上过点M的切线”与“求曲线
上过点M的切线”与“求曲线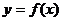 上在点M处的切线”;
上在点M处的切线”;
前者只要求切线过M点,M点未必是切点;而后者则很明确,切点就是M点。
[举例]求函数y=x3-3x2+x的图象上过原点的切线方程
解析:易见O(0,0)在函数y=x3-3x2+x的图象上,y’=3x2-6x+1,但O点未必是切点。
设切点A(x0,y0)∵y’=3x2-6x+1, ∴切线斜率为3x02-6x0+1,又切线过原点,∴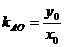 =3x02-6x0+1即:y0=3x03-6x02+x0 ①
=3x02-6x0+1即:y0=3x03-6x02+x0 ①
又∵切点A(x0,y0)y=x3-3x2+x的图象上∴y0=x03-3x02+x0 ②
由①②得:x0 =0或x0 =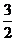 ,∴切线方程为:y=x或5x+4y=0
,∴切线方程为:y=x或5x+4y=0
点评:一般地,过三次曲线的对称中心(不难证明三次曲线一定是中心对称图形,且对称中心在曲线上)的切线有且仅有一条;而过三次曲线上除对称中心外的任一点的切线有二条。以下给出简单证明(不要求学生掌握):由于三次曲线都是中心对称曲线,因此,将其对称中心移至坐标原点便可将三次函数的解析式简化为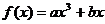 。若M(x1,y1)是三次曲线
。若M(x1,y1)是三次曲线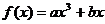 上的任一点,设过M的切线与曲线y=f(x)相切于(x0,y0),则切线方程为
上的任一点,设过M的切线与曲线y=f(x)相切于(x0,y0),则切线方程为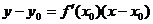 ,因点M上此切线上,故
,因点M上此切线上,故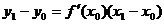 ,又
,又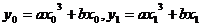 ,所以
,所以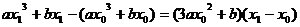 ,整理得:
,整理得: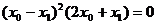 ,解得,
,解得,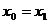 或
或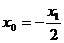 。 当点M是对称中心即
。 当点M是对称中心即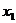 =
=
-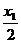 =0时,过点M作曲线的切线切点是惟一的,且为M,故只有一条切线;当点M不是对称中心即
=0时,过点M作曲线的切线切点是惟一的,且为M,故只有一条切线;当点M不是对称中心即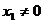 时,过点M作曲线的切线可产生两个不同的切点,故必有两条切线,其中一条就是以M为切点(亦即曲线在点M处)的切线。
时,过点M作曲线的切线可产生两个不同的切点,故必有两条切线,其中一条就是以M为切点(亦即曲线在点M处)的切线。
[巩固] 曲线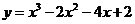 上过点
上过点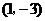 的切线方程是 .
的切线方程是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com