
2.试题全部答在“答题纸”上,答在试卷上无效。
第I卷 选择题(共48分)
在下列各题的四个选项中。只有一个选项最符合题意。(每小题2分,共48分。)
1.本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。全卷共100分。考试用时90分钟。
21.[解析](Ⅰ)将函数y=f(x+1)的图象向右平移一个单位,得到函数y=f(x)的图象,
∴函数y=f(x)的图象关于点(0, 0)对称,即函数y=f(x)是奇函数.……………………1分
∴f(x)=a1x3+a3x,∴f ' (x)=3a1x2+a3,
由题意得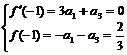 ,所以
,所以 ,
,
则f(x)=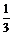 x3-x,经检验满足题意.………………………………………………………3分
x3-x,经检验满足题意.………………………………………………………3分
(Ⅱ)证明:由(Ⅰ)知g(x)=x,∴当x>0时,不等式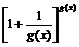 <e即为
<e即为
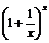 <e
<e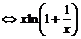 <1
<1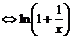 <
<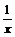 .…………………………………………5分
.…………………………………………5分
构造函数h(x)=ln(1+x)-x(x>0),则h' (x)=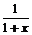 -1=
-1=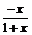 <0,
<0,
∴函数h(x)在(0, +∞)上是减函数.
∴x>0时,h(x)<h(0)=0,即x>0时,ln(1+x)<x成立,……………………………7分
用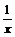 换x得,x>0时,
换x得,x>0时,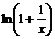 <
<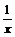 成立.∴当x>0时,
成立.∴当x>0时,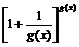 <e.……8分
<e.……8分
(Ⅲ) bn=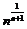 ,由(Ⅱ)
,由(Ⅱ)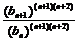 =
=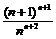 =
=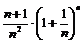 <
<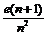 <
<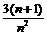 .…9分
.…9分
令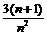 <1,得n2―3n―3>0,结合n∈N*得n≥4,
<1,得n2―3n―3>0,结合n∈N*得n≥4,
因此,当n≥4时,有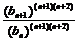 <1,
<1,
∴当n≥4时,bn>bn+1,即b4>b5>b6>…,……………………………………………10分
又通过比较b1、b2、b3、b4的大小知b1<b2<b3<b4.…………………………………11分
因为b1=1,且n≠1时,bn=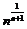 ≠1,
≠1,
所以若数列{ bn }中存在相等的两项,只能是b2、b3与后面的项可能相等.
又b2= =
=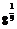 =b8,b3=
=b8,b3= >b5=
>b5=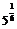 ,
,
所以数列{ bn }中存在唯一相等的两项,即b2=b8.………………13分
20.[解析]:(Ⅰ)依题意双曲线为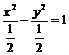 ,则
,则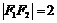 ,
,
∴ ,………………………………………………………………1分
,………………………………………………………………1分
∴点P的轨迹是以F1,F2为焦点的椭圆,其方程可设为 (a>b>0).…2分
(a>b>0).…2分
由2a=4,2c=2,得a=2,c=1,∴b2=4-1=3,则所求椭圆方程为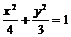 ,
,
故动点P的轨迹E的方程为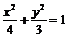 .…………………………………………………3分
.…………………………………………………3分
(Ⅱ)设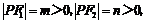 ∠F1PF2=
∠F1PF2=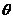 ,则由m+n=4,
,则由m+n=4,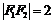 ,可知在△F1PF2中,
,可知在△F1PF2中,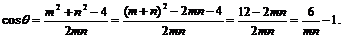 ………………………………5分
………………………………5分
又∵m>0,n>0,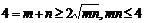 ,即
,即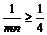 ,∴
,∴ 当且仅当m=n=2时等号成立. 故cos
F1PF2的最小值为
当且仅当m=n=2时等号成立. 故cos
F1PF2的最小值为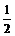 .……………………………………7分
.……………………………………7分
(Ⅲ) M (-2, 0).①当l与x轴重合时,构不成∠AMB,不合题意.…………………8分
②当l⊥x轴时,直线l的方程为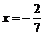 ,代入
,代入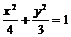 ,解得A、B的坐标分别为
,解得A、B的坐标分别为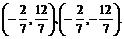 而
而 ∴∠AMB=90°.……………………………………9分
∴∠AMB=90°.……………………………………9分
猜测∠AMB=90°为定值,证明如下:
证明:设直线l方程为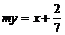 ,由
,由 得
得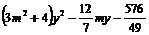 =0.…10分
=0.…10分
设点A(x1, y1),B(x2, y2),则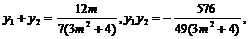 ………………11分
………………11分
∴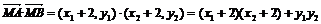
=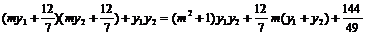
=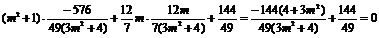 .
.
∴∠AMB=90°为定值(A、B与点M不重合).…………………………………………13分
19.[解析]:(Ⅰ)ξ的可能值为1,2,3,4,5.
P(ξ=1)= =
=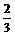 ;P(ξ=2)=
;P(ξ=2)= ×
× =
=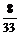 ;P(ξ=3)=
;P(ξ=3)= ×
× ×
× =
= ;
;
P(ξ=4)= ×
× ×
× ×
× =
= ;P(ξ=5)=
;P(ξ=5)= ×
× ×
× ×
×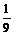 ×
×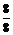 =
=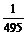 ;…………2分
;…………2分
ξ的分布列如下表:
|
ξ |
1 |
2 |
3 |
4 |
5 |
…………4分 |
|
P |
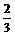 |
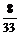 |
 |
 |
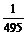 |
∴甲取球次数ξ的数学期望为Eξ=1×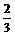 +2×
+2×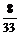 +3×
+3× +4×
+4× +5×
+5×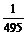 =
=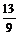 .……6分
.……6分
(Ⅱ)记“甲摸球一次摸出红球”为事件A,记“乙摸球一次摸出红球”为事件B,
则P(A)=P(B)=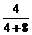 =
=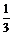 ,P(
,P(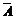 )=P(
)=P(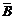 )=
)=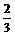 ,且A、B相互独立,
,且A、B相互独立,
根据摸球规则可知,第n次由甲摸球包括如下两个事件:
①第n-1次由甲摸球,且摸出红球,其发生的概率为an-1×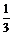 ;
;
②第n-1次由乙摸球,且摸出白球,其发生的概率为(1-an-1)×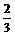 ;…………………8分
;…………………8分
∵上述两个事件互斥,∴an=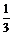 an-1+
an-1+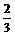 ×(1-an-1),an=-
×(1-an-1),an=-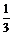 an-1+
an-1+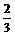 (n≥2),……9分
(n≥2),……9分
由an=-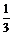 an-1+
an-1+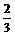 (n≥2)得an-
(n≥2)得an-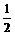 =-
=-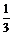 (an-1-
(an-1-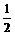 )(n≥2),………………………10分
)(n≥2),………………………10分
∵甲进行第一次摸球,∴a1=1,即a1-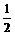 =
=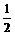 ,
,
∴数列{ an-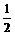 }是首项为
}是首项为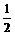 ,公比为-
,公比为-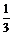 的等比数列,即an-
的等比数列,即an-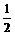 =
=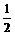 ×
×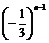 ,
,
∴an=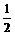 +
+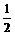 ×
×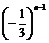 .……………………………………………………………………13分
.……………………………………………………………………13分
18.[解析]:
|
填湖面积 |
填湖及排水设备费 |
水面经济收益 |
填湖造地后收益 |
|
x(亩) |
ax2(元) |
bx |
cx |
(Ⅰ)收益不小于指出的条件可以表示为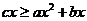 ,
,
所以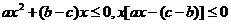 .……………………………………3分
.……………………………………3分
显然a>0,又c>b.
∴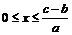 时,此时所填面积的最大值为
时,此时所填面积的最大值为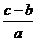 亩………………………………7分
亩………………………………7分
(Ⅱ)设该地现在水面m亩.今年填湖造地y亩,
则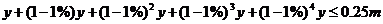 ,………………9分
,………………9分
即 ,所以
,所以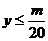 .
.
因此今年填湖造地面积最多只能占现有水面的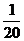 …………………………………12分
…………………………………12分
17.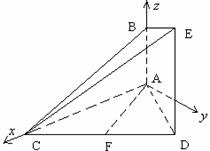 [解析]:设
[解析]:设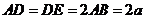 ,建立如图所示的坐标系
,建立如图所示的坐标系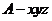 ,则
,则
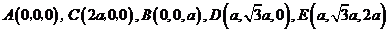 .
.
∵ 为
为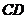 的中点,∴
的中点,∴ .……………2分
.……………2分
(Ⅰ)证明: 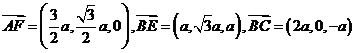 ,
,
∵ ,
,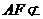 平面BCE,∴AF∥平面BCE.……………4分
平面BCE,∴AF∥平面BCE.……………4分
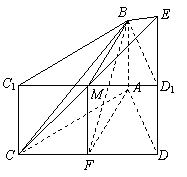 方法二:如右图,补成直棱柱ACD-BC1D1,则D1为DE中点,取C1D1中点M,可证M也为CE的中点,得平行四边形AFMB,则AF∥BM,可得AF∥平面BCE.
方法二:如右图,补成直棱柱ACD-BC1D1,则D1为DE中点,取C1D1中点M,可证M也为CE的中点,得平行四边形AFMB,则AF∥BM,可得AF∥平面BCE.
(Ⅱ)证明: ∵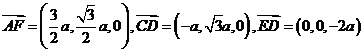 ,
,
∴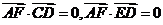 ,∴
,∴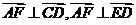 .
.
又CD∩ED=D,∴AF⊥平面CDE,又AF∥平面BCE,…7分
∴平面BCE⊥平面CDE.……………………………………………………………8分
方法二:证AF⊥平面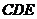 ,由(Ⅰ) AF∥BM,BM
,由(Ⅰ) AF∥BM,BM 平面
平面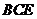 .∴平面
.∴平面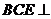 平面
平面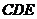 .
.
(Ⅲ)解:设平面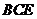 的法向量为
的法向量为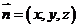 ,由
,由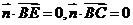 可得:
可得:
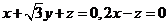 ,取
,取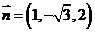 .………………………………9分
.………………………………9分
又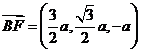 ,设
,设 和平面
和平面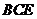 所成的角为
所成的角为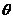 ,则sin
,则sin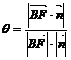 =
=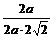 =
=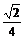 .
.
∴直线 和平面
和平面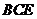 所成角的正弦值为
所成角的正弦值为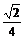 . …………………………………12分
. …………………………………12分
16.[解析]:(Ⅰ)∵m=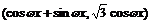 ,n=
,n=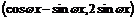 (ω>0),
(ω>0),
∴f(x)=m·n= …………………………………………2分
…………………………………………2分
∴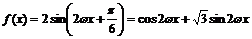 .
.
∵函数f(x)的周期为π,∴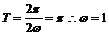 .…………………………………………5分
.…………………………………………5分
(Ⅱ)在△ABC中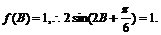 ∴
∴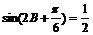 .………………………6分
.………………………6分
又∵0<B<π,∴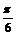 <2B+
<2B+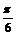 <
<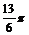 .∴2B+
.∴2B+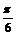 =
=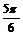 .∴B=
.∴B= .………………8分
.………………8分
∵a,b,c成等差数列,∴2b=a+c.…………………………………………………9分
∴cosB=cos =
=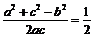 , ∴
, ∴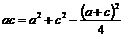 .
.
化简得a=c,……………………………………………………………………………11分
又∵B= ,∴△ABC为正三角形.…………………………………………………12分
,∴△ABC为正三角形.…………………………………………………12分
9.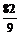 ; 10.[-7, 9]; 11.
; 10.[-7, 9]; 11. ;12.6;13.
;12.6;13.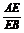 =
=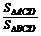 ;14.①③④;15.7;(2, 3).
;14.①③④;15.7;(2, 3).
1.B 2.D 3.A 4.B 5.D 6.C 7.D 8.A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com