
第Ⅱ卷(非选择题共100分)
22.(本小题满分15分)
已知函数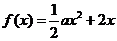 ,
,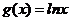 .
.
(Ⅰ)如果函数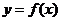 在
在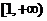 上是单调增函数,求
上是单调增函数,求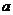 的取值范围;
的取值范围;
(Ⅱ)是否存在实数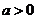 ,使得方程
,使得方程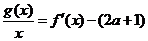 在区间
在区间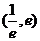 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出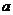 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
杭师大附中2010届学年高三年级第五次月考答题卷
第Ⅰ卷(选择题 共50分)
21.(本小题满分15分)
椭圆C的中心在坐标原点O,焦点在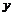 轴上,离心率为
轴上,离心率为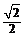 ,以短轴的一个端点与两焦点为顶点的三角形的面积为
,以短轴的一个端点与两焦点为顶点的三角形的面积为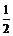
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点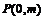 存在直线
存在直线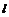 与椭圆C交于相异两点A,B,满足:
与椭圆C交于相异两点A,B,满足: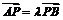 且
且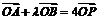 ,求常数
,求常数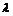 的值和实数
的值和实数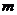 的取值范围.
的取值范围.
20.(本小题满分14分)
射击运动员在双向飞碟射击比赛中,每轮比赛连续发射两枪,击中两个飞靶得2分,击中一个得1分,未击中得0分。某运动员在每轮比赛时,第一枪命中率为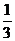 ,第二枪命中率为
,第二枪命中率为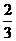 ,该运动员只进行两轮比赛。
,该运动员只进行两轮比赛。
(Ⅰ)求该运动员得4分的概率;
(Ⅱ)若该运动员所得分数为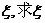 的分布列及数学期望。
的分布列及数学期望。
19.(本大题共14分)
如图所示,ABCD为矩形,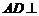 平面ABE,
平面ABE,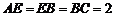 ,F为CE上的点,且
,F为CE上的点,且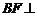 平面ACE.
平面ACE.
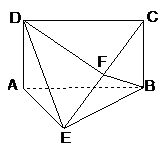 (Ⅰ)求证:
(Ⅰ)求证: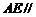 平面BFD;
平面BFD;
(Ⅱ)求证: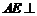 平面BCE;
平面BCE;
(III) 求平面BDF与平面ABE所成的二面角的平面角.
18.(本小题满分14分)
在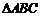 中,角
中,角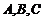 的对边分别为
的对边分别为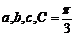 ,
,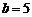 ,
,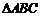 的面积为
的面积为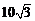 .
.
(Ⅰ)求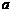 ,
,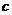 的值;
的值;
(Ⅱ)求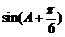 的值.
的值.
17.下列给出的四个命题中:
①已知数列 ,那么对任意的
,那么对任意的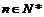 ,点
,点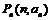 都在直线
都在直线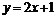 上是
上是 为等差数列的充分不必要条件;
为等差数列的充分不必要条件;
②“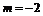 ”是“直线
”是“直线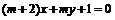 与直线
与直线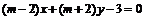 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③设圆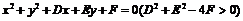 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为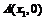 ,
,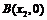 ,
,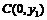 ,
,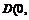
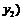 ,则
,则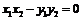 ;
;
④将函数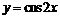 的图像向右平移
的图像向右平移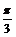 个单位,得到函数
个单位,得到函数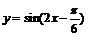 的图像.
的图像.
其中为真命题的是______________________(填序号).
16.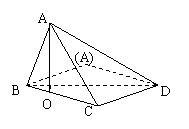 如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使A点在平面BCD内的射影落在BC边上,若二面角C-AB-D的平面角大小为θ,则
如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将△ABD折起,使A点在平面BCD内的射影落在BC边上,若二面角C-AB-D的平面角大小为θ,则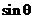 的值等于
的值等于
15.已知函数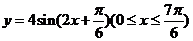 的图象与一条平行于x轴的直线有三个交点,其横坐标分别为
的图象与一条平行于x轴的直线有三个交点,其横坐标分别为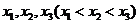 ,则
,则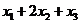 =
.
=
.
14.以双曲线的焦点为圆心,实半轴长为半径的圆与双曲线的渐近线相切,则双曲线的离心率为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com