
要使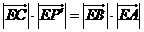 ,则只需
,则只需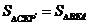 ,即
,即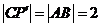 .而
.而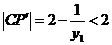 ,因此不存在点E使得
,因此不存在点E使得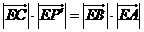 成立.
成立.
由此可得: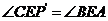 .
.
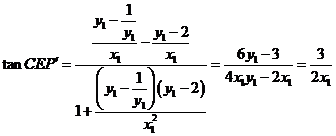 (其中用到
(其中用到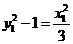 代换)
代换)
(Ⅳ) 先证: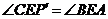
(Ⅲ)点E处曲线Q的切线的斜率为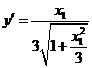 ,则切线方程为
,则切线方程为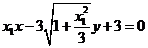 ,AE、BF的方程为
,AE、BF的方程为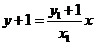 ,
,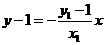 ,则
,则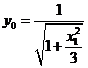 ,所以
,所以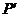 在上述切线上,即过点
在上述切线上,即过点 和点E的直线是曲线Q的一条切线.
和点E的直线是曲线Q的一条切线.
(Ⅱ)由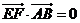 可设点
可设点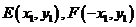 则由A、P、E三点共线可得
则由A、P、E三点共线可得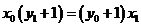 ,同理可得:
,同理可得: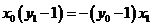 ,两式相乘得:
,两式相乘得: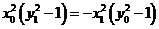 ,又因为
,又因为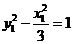 ,所以
,所以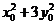 =3
=3
化简得: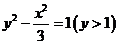
所以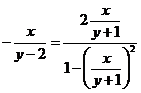 或
或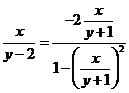
解:(Ⅰ)设动点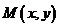 ,因为
,因为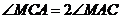
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com