9．学会把三等分角问题代数化。

8．给定长为a的线段,会用尺规作图方法作出长为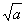的线段。

7．给出一些数域、扩域的具体实例。

6．设F是一数域k∈F，且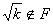。证明：集合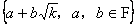也是一个数域，且F是集合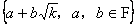的子集合。了解扩域的概念。

5．通过有理数对加、减、乘、除运算的封闭性，了解有理数域和一般数域的概念。

4．对于给定的任何已知线段，若把它作为单位长,则任一(正)有理数是可作图的(即仅用圆规和直尺可作出该有理数长的线段)。

3．给定线段a,b,会用尺规作图方法作出长为a+b，a-b，ab，a/b的线段。

2．理解解决三等分角问题的基本思路──刻画尺规作图的范围。

1．了解古希腊三大几何作图问题，通过三等分角问题了解它们的正确提法。在不限于圆规和直尺的前提下，了解三等分角的几种不同作法。

5．在介绍拓扑学应用时，应注重对拓扑思想方法的介绍，不追求严格化的叙述。

三等分角与数域扩充

三等分角问题、倍方问题和化圆为方问题被称为古希腊的三大几何作图问题。解决这类问题的思想方法不仅在数学上,而且在人类的思想史上都具有重大意义。

本专题将通过对三等分角问题的讨论使学生了解解决这类问题的基本思想方法，并能用此方法解决倍方问题和仅用圆规直尺不能作正七边形的问题。另外还介绍用代数方法讨论正十七边形是可作图的(即可用尺规作图方法作出正十七边形)。通过以上的讨论，使学生体会和理解其中蕴涵的数学思想方法，提高分析和解决数学问题的能力。

内容与要求