
5.通过命题演算的学习,了解什么是命题和命题的取值。认识什么是两个命题的“或命题”和“且命题”,什么是一个命题的“非命题”(“否定命题”)、这些新命题的取值是怎样确定的。
4.理解任意电路都可以用一个电路函数来表示,而电路函数又都可以用一个电路多项式实现。
3.通过状态和状态的运算,抽象出布尔代数、电路函数和电路多项式的概念。感悟从实际问题抽象、概括为数学问题的过程和用数学理论解决实际问题的思想方法。
2.通过对开关电路的分析,认识新电路的状态是由原电路的状态通过运算形成的。掌握状态和状态的运算两个概念。
1.通过开关电路知道电路和电路的两种状态以及它们的数学表示。知道什么是两个电路的并联和串联,什么是逆反电路,以及它们的状态是怎样确定的。
4.马尔可夫型决策具有广泛的应用,高中学生可以通过例子加以理解,并掌握其方法,不要在一般理论和方法的水平上展开。
开关电路与布尔代数
高度的抽象性及其带来的符号化、形式化是数学的基本特征之一。不同的实际问题经抽象、概括后,可得到相同的数学概念、运算法则,乃至同一数学理论。反之,同一数学概念、运算法则和数学理论可应用到表面看来完全不同的实际问题中。
布尔代数是由布尔(G.Boole)于1847年引入,用以研究命题演算的数学理论。后来,美国电气工程师申农指出,可以用布尔代数来研究开关电路及其相关问题。
本专题以设计由三人控制一个电灯的电路为背景,从开关电路设计,提出一个具体问题,将电路设计数学化为电路代数和电路多项式,再数学地研究电路和电路多项式,完全解决最初提出的问题,完整地给出一个电路代数的数学模型,这也是布尔代数的一个实际应用,从中可感受到数学化的抽象过程,以及数学理论的应用价值。
由电路的“并”“串”联和“逆反”产生的新电路的状态{0,1}是由原电路的状态{0,1},经过运算+、×和余(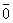 =1,
=1,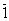 =0)得到的。此外,本专题中关于由简单命题通过“或”“且”和“非”(“否定”)组成的新命题的真与伪,也是由原命题的真与伪,经过运算+、×和余(
=0)得到的。此外,本专题中关于由简单命题通过“或”“且”和“非”(“否定”)组成的新命题的真与伪,也是由原命题的真与伪,经过运算+、×和余(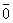 =1,
=1,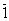 =0)得到的。它们是一脉相承的。这些运算与中学数学所学的数与多项式的运算也有相似之处。因此,本专题的学习对中学生深入认识数与多项式的本质也是非常有益的。
=0)得到的。它们是一脉相承的。这些运算与中学数学所学的数与多项式的运算也有相似之处。因此,本专题的学习对中学生深入认识数与多项式的本质也是非常有益的。
内容与要求
3.通过决策过程中概率估计的不精确性,理解灵敏度分析的必要性。
2.先通过实例理解风险决策的概念,学会决策的初步方法;然后通过对具体例子分析,介绍损益函数和损益矩阵,理解决策树的作用以及掌握用决策树进行决策的方法。
1.整个专题应该以多种实例为主线展开,帮助学生理解决策应用的广泛性,理解决策的结果具有风险性以及它的实际意义和有效性。概念应当尽可能少,只是在必要时引入。方法应该通过具体的例子进行介绍,在此基础上辅以必要的推广和总结。
6.完成一个学习总结报告。报告应包括三方面的内容:(1)知识的总结。对本专题的整体思路、结构和内容的理解,对风险决策方法及其意义的认识。(2)拓展。通过查阅资料、调查研究、访问求教、独立思考,对某些内容、某些结果和应用进行拓展和深入。(3)对本专题的感受、体会、看法。
说明与建议
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com