
19.(本小题满分16分)
将9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为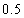 。若一个坑内至少有一粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。(本题的计算结果都精确到
。若一个坑内至少有一粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。(本题的计算结果都精确到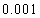 )
)
(1)求甲坑不需要补种的概率;
(2)求3个坑中恰有1个坑不需要补种的概率;
(3)求有坑需要补种的概率.
18.(本小题满分16分)
用6种不同颜色为图中两块(甲,乙)广告牌着色,要求在①、②、③、④四个区域中每个格子涂一种颜色且相邻(有公共边界)的区域不用同一种颜色.
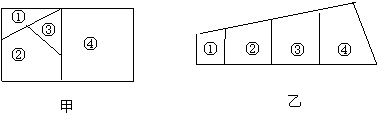
(1)求为甲着色时共有多少种不同的方法?
(2)若为乙着色时最多使用其中的三种颜色,求不同的涂色方法共有多少种?
17.(本小题满分14分)
给定矩阵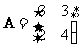 及向量
及向量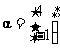 .[
.[
(1)求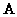 的特征值
的特征值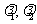 (
(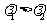 );
);
(2)求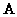 属于
属于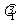 的特征向量
的特征向量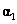 及属于
及属于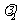 的特征向量
的特征向量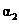 ;
;
(3)计算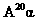 .
.
16.(本小题满分14分)
某食品企业一个月内被消费者投诉的次数用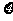 表示,椐统计,随机变量
表示,椐统计,随机变量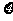 的概率分布如下:
的概率分布如下:
 |
0 |
1 |
2 |
3 |
|
p |
0.1 |
0.3 |
2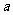 |
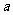 |
(1)求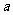 的值和
的值和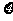 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
15.(本小题满分14分)
已知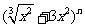 的展开式中,各项的系数和比它的二项式系数和大992.
的展开式中,各项的系数和比它的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.[
14.有四位同学在同一天的上、下午参加A、B、C、D、E的五个项目的测试,每位同学上、下午各测试其中的一项,且不重复,若上午不测D项目,下午不测E项目,其余项目上、下午都各测试一人,则不同的安排方式共有 ★ 种(用数字作答).
13.下面结论正确的序号是 ★ .
①在极坐标系中,点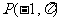 在曲线
在曲线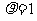 上;
上;
②用反证法证明“若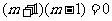 ,则
,则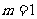 或
或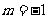 ”时,应假设
”时,应假设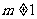 或
或 ;③已知函数
;③已知函数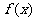 (
(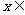 R)满足
R)满足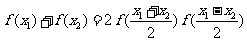 ,且
,且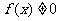 ,则
,则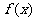 是偶函数;
是偶函数;
④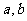 都是整数,且
都是整数,且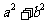 能被3整除,则
能被3整除,则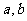 都能被3整除.
都能被3整除.
12.设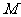 是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换,则椭圆
是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换,则椭圆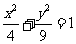 在
在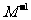 的作用下的新曲线的方程是 ★ .
的作用下的新曲线的方程是 ★ .
11.已知曲线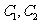 的极坐标方程分别为
的极坐标方程分别为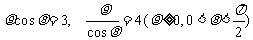 ,则
,则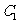 与
与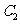 交点的极坐标为 ★ .
交点的极坐标为 ★ .
10.直线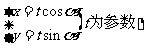 与圆
与圆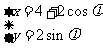 (
(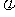 为参数)相切,则此直线的倾斜角
为参数)相切,则此直线的倾斜角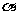 = ★ .
= ★ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com