9．通过一些简单问题了解证明不等式的基本方法：比较法、综合法、分析法、反证法、放缩法。

8．会用上述不等式证明一些简单问题。能够利用平均值不等式、柯西不等式求一些特定函数的极值。

7．会用数学归纳法证明贝努利不等式：

　(1+x)ⁿ＞1+nx(x＞－1，x≠0，n为正整数)。

　了解当n为实数时贝努利不等式也成立。

6．了解数学归纳法的原理及其使用范围，会用数学归纳法证明一些简单问题。

5．用向量递归方法讨论排序不等式。

4．用参数配方法讨论柯西不等式的一般情况：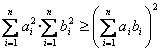

3．认识柯西不等式的几种不同形式。理解它们的几何意义。

　(1)证明：柯西不等式向量形式：|α||β|≥|α·β|。

　(2)证明：(a²+b²)(c²+d²)≥(ac+bd)²。

　(3)证明：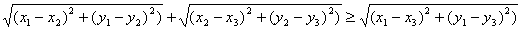

　(通常称作平面三角不等式)。

2．理解绝对值的几何意义，并能利用绝对值不等式的几何意义证明以下不等式：

　(1)∣a+b∣≤∣a∣+∣b∣；

　(2)∣a－b∣≤∣a－c∣+∣c－b∣；

　(3)会利用绝对值的几何意义求解以下类型的不等式：

　∣ax+b∣≤c；

　∣ax+b∣≥c；

　∣x－c∣+∣x－b∣≥a。

1．回顾和复习不等式的基本性质和基本不等式。

6．可以应用计算机展现心脏线、螺线、玫瑰线、叶形线、摆线、渐开线等，使学生感受这些曲线的美。

　不等式选讲

　在自然界中存在着大量的不等量关系和等量关系，不等关系和相等关系是基本的数学关系。它们在数学研究和数学应用中起着重要的作用。

　本专题将介绍一些重要的不等式和它们的证明、数学归纳法和它的简单应用。本专题特别强调不等式及其证明的几何意义与背景，以加深学生对这些不等式的数学本质的理解，提高学生的逻辑思维能力和分析解决问题的能力。

　内容与要求