1．计数原理(约14课时)

　(1)分类加法计数原理、分步乘法计数原理

　通过实例，总结出分类加法计数原理、分步乘法计数原理；能根据具体问题的特征，选择分类加法计数原理或分步乘法计数原理解决一些简单的实际问题。

　(2)排列与组合

　通过实例，理解排列、组合的概念；能利用计数原理推导排列数公式、组合数公式，并能解决简单的实际问题。

　(3)二项式定理

　能用计数原理证明二项式定理(参见例1)； 会用二项式定理解决与二项展开式有关的简单问题。

7．在复数概念与运算的教学中，应注意避免繁琐的计算与技巧训练。对于感兴趣的学生，可以安排一些引申的内容，如求x³=1的根，介绍代数学基本定理等。

　参考案例

例1 一个物体依照s＝s(t)规律在直线上运动，我们已经知道，其在某一时刻的t₀运动速度v(t₀)(即瞬时速度或瞬时变化率)为s＝s(t)在t₀时刻的导数，即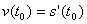。今考虑s(t)在t＝a到t＝b之间位置的总变化。我们把区间a≤t≤b分割成个小区间，不妨假设小区间的长度相等，其长度为Δt_i。对每一个小区间，我们假设的变化率近似为某一常量，于是我们可以说Δs≈s(t)的变化率×时间在第一个小区间内，即从t₀到t₁，假设s(t)的变化率近似地为s'(t₀)，于是有

同样，在第二个小区间，即从₁到₂，假设s(t)的变化率近似地为s'(t₁)，因此有

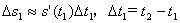
等等。把所有小区间上得到的位置变化近似值全部加在一起，得到

我们可以把s(t)在t₀＝a到t_n＝b之间位置的总变化写成s(b)－s(a)。另一方面，当分割无限加细，n趋于无空时，和式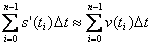

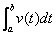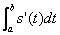的极限就是定积分或，也就是s(t)在t＝a到t＝b之间位置的总变化。于是，我们可得到以下结论：

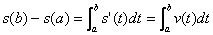
也就是说，变化率的定积分给出了总的变化。

特别地，当物体作匀速运动时，即

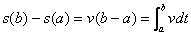
当物体作匀加速运动时，即v(t)＝at(其中a是常数)时，v(t)≡v时

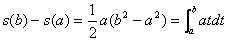
一般地，如果f(t)是连续函数，并且f(t)＝F'(t)，那么

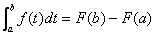
　这就是微积分基本定理。这里给出的并不是非常严格的证明，但是，它反映了微积分基本定理的基本思想，反映了微分(导数)与积分的联系。

　选修2-3

　在本模块中，学生将学习计数原理、统计案例、概率。

　计数问题是数学中的重要研究对象之一，分类加法计数原理、分步乘法计数原理是解决计数问题的最基本、最重要的方法，也称为基本计数原理，它们为解决很多实际问题提供了思想和工具。在本模块中，学生将学习计数基本原理、排列、组合、二项式定理及其应用，了解计数与现实生活的联系，会解决简单的计数问题。

　学生将在必修课程学习概率的基础上，学习某些离散型随机变量分布列及其均值、方差等内容，初步学会利用离散型随机变量思想描述和分析某些随机现象的方法，并能用所学知识解决一些简单的实际问题，进一步体会概率模型的作用及运用概率思考问题的特点，初步形成用随机观念观察、分析问题的意识。

　学生将在必修课程学习统计的基础上，通过对典型案例的讨论，了解和使用一些常用的统计方法，进一步体会运用统计方法解决实际问题的基本思想，认识统计方法在决策中的作用。

　内容与要求

6．教师应借助具体实例让学生了解数学归纳法的原理，对证明的问题要控制难度。

5．本模块中设置的证明内容是对学生已学过的基本证明方法的总结。在教学中，应通过实例，引导学生认识各种证明方法的特点，体会证明的必要性。对证明的技巧性不宜作过高的要求。

4．教学中应通过实例，引导学生运用合情推理去探索、猜测一些数学结论，并用演绎推理确认所得结论的正确性，或者用反例推翻错误的猜想。教学的重点在于通过具体实例理解合情推理与演绎推理，而不追求对概念的抽象表述。

3．教师应引导学生在解决具体问题的过程中，将研究函数的导数方法与初等方法作比较，以体会导数方法在研究函数性质中的一般性和有效性。

2．在教学中，要防止将导数仅仅作为一些规则和步骤来学习，而忽视它的思想和价值。应使学生认识到，任何事物的变化率都可以用导数来描述。

1．本模块中，导数的概念是通过实际背景和具体应用的实例引入的。教学中，可以通过研究增长率、膨胀率、效率、密度、速度等反映导数应用的实例，引导学生经历由平均变化率到瞬时变化率的过程，知道瞬时变化率就是导数。通过感受导数在研究函数和解决实际问题中的作用，体会导数的思想及其内涵。这样处理的目的是帮助学生直观理解导数的背景、思想和作用。

3．数系的扩充与复数的引入(约4课时)

　(1)在问题情境中了解数系的扩充过程，体会实际需求与数学内部的矛盾(数的运算规则、方程理论)在数系扩充过程中的作用，感受人类理性思维的作用以及数与现实世界的联系。

　(2)理解复数的基本概念以及复数相等的充要条件。

　(3)了解复数的代数表示法及其几何意义。

　(4)能进行复数代数形式的四则运算，了解复数代数形式的加、减运算的几何意义。

　说明与建议

2．推理与证明(约8课时)

　(1)合情推理与演绎推理

　①结合已学过的数学实例和生活中的实例，了解合情推理的含义，能利用归纳和类比等进行简单的推理，体会并认识合情推理在数学发现中的作用(参见选修2-2案例中的例2、例3)。

　②结合已学过的数学实例和生活中的实例，体会演绎推理的重要性，掌握演绎推理的基本模式，并能运用它们进行一些简单推理。

　③通过具体实例，了解合情推理和演绎推理之间的联系和差异。

　(2)直接证明与间接证明

　①结合已经学过的数学实例，了解直接证明的两种基本方法：分析法和综合法；了解分析法和综合法的思考过程、特点。

　②结合已经学过的数学实例，了解间接证明的一种基本方法──反证法；了解反证法的思考过程、特点。

　(3)数学归纳法

　了解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题。

　(4)数学文化

　①通过对实例的介绍(如欧几里得《几何原本》、马克思《资本论》、杰弗逊《独立宣言》、牛顿三定律)，体会公理化思想。

　②介绍计算机在自动推理领域和数学证明中的作用。