
19.某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为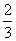 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为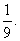
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为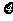 ,求
,求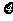 的分布列与均值E
的分布列与均值E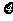 .
.
18.如图1所示,在边长为12的正方形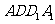 中,点
中,点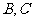 在线段
在线段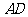 上,且
上,且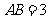 ,
,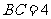 ,作
,作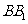
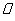
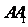 ,分别交
,分别交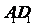 ,
,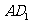 于点
于点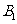 ,
,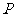 ,作
,作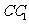
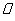
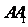 ,分别交
,分别交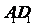 ,
,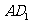 于点
于点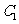 ,
,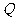 ,将该正方形沿
,将该正方形沿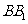 ,
,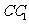 折叠,使得
折叠,使得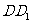 与
与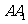 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱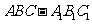 .
.
(Ⅰ)求证: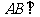 平面
平面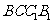 ;(Ⅱ)求四棱锥
;(Ⅱ)求四棱锥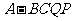 的体积;
的体积;

 (Ⅲ)求平面
(Ⅲ)求平面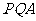 与平面
与平面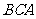 所成锐二面角的余弦值.
所成锐二面角的余弦值.
17.设函数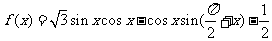 .
.
(Ⅰ)求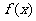 的最小正周期;
的最小正周期;
(Ⅱ)当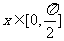 时,求函数
时,求函数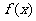 的最大值和最小值.
的最大值和最小值.
16.已知有公共焦点的椭圆与双曲线中心在原点,焦点在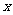 轴上,左右焦点分别为
轴上,左右焦点分别为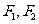 ,且它们在第一象限的交点为
,且它们在第一象限的交点为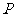 ,
,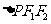 是以
是以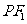 为底边的等腰三角形,若
为底边的等腰三角形,若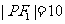 ,双曲线的离心率的取值范围为
,双曲线的离心率的取值范围为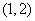 ,则该椭圆的离心率的取值范围为 .
,则该椭圆的离心率的取值范围为 .
15.在三棱锥A-BCD中,P、Q分别是棱AC、BD上的点,连结AQ、CQ、BP、DP、PQ,若三棱锥A-BPQ、B-CPQ、C-DPQ的体积分别为6、2、8,则三棱锥A-BCD的体积为 .
13.已知数列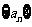 中,
中,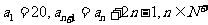 则数列
则数列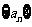 的通项公式是 . 14.已知双曲线
的通项公式是 . 14.已知双曲线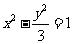 的左顶点为
的左顶点为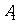 ,右焦点为
,右焦点为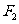 ,
,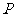 为双曲线右支上一点,则
为双曲线右支上一点,则 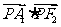 最小值为
.
最小值为
.
12.抛物线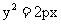
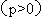 的焦点为F,点A、B在抛物线上,且
的焦点为F,点A、B在抛物线上,且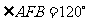 ,弦AB中点M在准线l上的射影为
,弦AB中点M在准线l上的射影为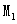 ,则
,则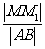 的最大值为( )
的最大值为( )
A. 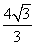 B.
B. 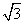 C.
C. 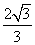 D.
D. 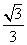
11.一个正四棱柱的底面边长为8,高为6,在其内部的底面上放入四个大小相同的球,使相邻的两球彼此相切,并且都与相邻的侧面相切,在四个球的上面再放一个球,使这个球在正四棱柱内部,则这个球半径的最大值为( )
A. 2
B.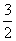 C.
C.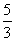 D.
D.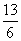
10.已知整数以按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1)……,则第60个数对是( )
A.(10,1) B.(2,10) C.(5,7) D.(7,5)
9. 定义在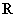 上的函数
上的函数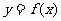 是减函数,且函数
是减函数,且函数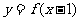 的图象关于
的图象关于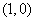 成中心对称,若
成中心对称,若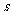 ,
,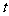 满足不等式
满足不等式 .则当
.则当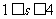 时,
时,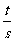 的取值范围是( )
的取值范围是( )
A.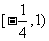 B.
B.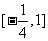 C.
C.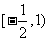 D.
D.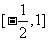
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com