
1.导数及其应用(约24课时)
(1)导数概念及其几何意义
① 通过对大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,知道瞬时变化率就是导数,体会导数的思想及其内涵(参见选修1-1案例中的例2、例3)。
②通过函数图象直观地理解导数的几何意义。
(2)导数的运算
① 能根据导数定义求函数y=c,y=x,y=x2,y=x3,y=1/x, y=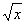 的导数。
的导数。
② 能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如f(ax+b))的导数。
③ 会使用导数公式表。
(3)导数在研究函数中的应用
① 结合实例,借助几何直观探索并了解函数的单调性与导数的关系(参见选修1-1案例中的例4);能利用导数研究函数的单调性,会求不超过三次的多项式函数的单调区间。
② 结合函数的图象,了解函数在某点取得极值的必要条件和充分条件;会用导数求不超过三次的多项式函数的极大值、极小值,以及闭区间上不超过三次的多项式函数最大值、最小值;体会导数方法在研究函数性质中的一般性和有效性。
(4)生活中的优化问题举例。
例如,通过使利润最大、用料最省、效率最高等优化问题,体会导数在解决实际问题中的作用。(参见选修1-1案例中的例5)
(5)定积分与微积分基本定理
① 通过实例(如求曲边梯形的面积、变力做功等),从问题情境中了解定积分的实际背景;借助几何直观体会定积分的基本思想,初步了解定积分的概念。
② 通过实例(如变速运动物体在某段时间内的速度与路程的关系),直观了解微积分基本定理的含义。(参见例1)
(6)数学文化
收集有关微积分创立的时代背景和有关人物的资料,并进行交流;体会微积分的建立在人类文化发展中的意义和价值。具体要求见本标准中“数学文化”的要求。(参见第91页)
6.在教学中,可以鼓励学生灵活选择运用向量方法与综合方法,从不同角度解决立体几何问题。
参考案例
例1 已知直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,︱BC︱=1,︱AA1︱=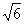 ,M是棱CC1的中点,证明:AB1⊥A1M。
,M是棱CC1的中点,证明:AB1⊥A1M。
例2 已知矩形ABCD和矩形ADEF垂直,以AD为公共边,但它们不在同一平面上。点M,N分别在对角线BD,AE上,且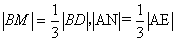 。证明:MN∥平面CDE。
。证明:MN∥平面CDE。
例3 已知单位正方体ABCD-A1B1C1D1,E,F 分别是棱B1C1和C1D1的中点。试求:
① AD1与所成的角;
② AF与平面BEB1所成的角;
③ 二面角C1-DB-B1的大小。
选修2-2
在本模块中,学生将学习导数及其应用、推理与证明、数系的扩充与复数的引入。
微积分的创立是数学发展中的里程碑,它的发展和广泛应用开创了向近代数学过渡的新时期,为研究变量和函数提供了重要的方法和手段。导数概念是微积分的核心概念之一,它有极其丰富的实际背景和广泛的应用。在本模块中,学生将通过大量实例,经历由平均变化率到瞬时变化率刻画现实问题的过程,理解导数概念,了解导数在研究函数的单调性、极值等性质中的作用,初步了解定积分的概念,为以后进一步学习微积分打下基础。通过该模块的学习,学生将体会导数的思想及其丰富内涵,感受导数在解决实际问题中的作用,了解微积分的文化价值。
“推理与证明”是数学的基本思维过程,也是人们学习和生活中经常使用的思维方式。推理一般包括合情推理和演绎推理。合情推理是根据已有的事实和正确的结论(包括定义、公理、定理等)、实验和实践的结果,以及个人的经验和直觉等推测某些结果的推理过程,归纳、类比是合情推理常用的思维方法。在解决问题的过程中,合情推理具有猜测和发现结论、探索和提供思路的作用,有利于创新意识的培养。演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等),按照严格的逻辑法则得到新结论的推理过程,培养和提高学生的演绎推理或逻辑证明的能力是高中数学课程的重要目标,合情推理和演绎推理之间联系紧密、相辅相成。证明通常包括逻辑证明和实验、实践证明,数学结论的正确性必须通过逻辑证明来保证,即在前提正确的基础上,通过正确使用推理规则得出结论。在本模块中,学生将通过对已学知识的回顾,进一步体会合情推理、演绎推理以及二者之间的联系与差异;体会数学证明的特点,了解数学证明的基本方法,包括直接证明的方法(如分析法、综合法、数学归纳法)和间接证明的方法(如反证法);感受逻辑证明在数学以及日常生活中的作用,养成言之有理、论证有据的习惯。
数系扩充的过程体现了数学的发现和创造过程,同时体现了数学发生发展的客观需求和背景,复数的引入是中学阶段数系的又一次扩充。在本模块中,学生将在问题情境中了解数系扩充的过程以及引入复数的必要性,学习复数的一些基本知识,体会数系扩充中人类理性思维的作用。
内容与要求
5.空间向量的教学应引导学生运用类比的方法,经历向量及其运算由平面向空间推广的过程。教学过程中应注意维数增加所带来的影响。
4.曲线与方程的教学应以学习过的曲线为主,注重使学生体会曲线与方程的对应关系,感受数形结合的基本思想。对于感兴趣的学生,教师也可以引导学生了解圆锥曲线的离心率与统一方程。有条件的学校应充分发挥现代教育技术的作用,通过一些软件向学生演示方程中参数的变化对方程所表示的曲线的影响,使学生进一步理解曲线与方程的关系。
3.教师可以向学生展现圆锥曲线在实际中的应用,例如,投掷铅球的运行轨迹、卫星的运行轨迹。
2.在引入圆锥曲线时,应通过丰富的实例(如行星运行轨道、抛物运动轨迹、探照灯的镜面),使学生了解圆锥曲线的背景与应用。
教师应向学生展示平面截圆锥得到椭圆的过程,使学生加深对圆锥曲线的理解。有条件的学校应充分发挥现代教育技术的作用,利用计算机演示平面截圆锥所得的圆锥曲线(参见选修1-1案例中的例1)。
1.在常用逻辑用语教学中,应特别注意以下几个问题。
(1)这里考虑的命题是指明确地给出条件和结论的命题,对“命题的逆命题、否命题与逆否命题”只要求做一般性了解,重点关注四种命题的相互关系和命题的必要条件、充分条件、充要条件。
(2)对逻辑联结词“或”“且”“非”的含义,只要求通过数学实例加以了解,帮助学生正确地表述相关的数学内容。
(3)对于量词,重在理解它们的含义,不要追求它们的形式化定义。
(4)注意引导学生在使用常用逻辑用语的过程中,掌握常用逻辑用语的用法,纠正出现的逻辑错误,体会运用常用逻辑用语表述数学内容的准确性、简洁性。避免对逻辑用语的机械记忆和抽象解释,不要求使用真值表。
3.空间向量与立体几何(约12课时)
(1)空间向量及其运算
① 经历向量及其运算由平面向空间推广的过程。
② 了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示。
③ 掌握空间向量的线性运算及其坐标表示。
④ 掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。
(2)空间向量的应用
① 理解直线的方向向量与平面的法向量。
② 能用向量语言表述线线、线面、面面的垂直、平行关系。
③ 能用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理)(参见例1、例2、例3)。
④ 能用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。
说明与建议
2.圆锥曲线与方程(约16课时)
(1)圆锥曲线
① 了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用。
② 经历从具体情境中抽象出椭圆、抛物线模型的过程,掌握它们的定义、标准方程、几何图形及简单性质。
③ 了解双曲线的定义、几何图形和标准方程,知道双曲线的有关性质。
④ 能用坐标法解决一些与圆锥曲线有关的简单几何问题(直线与圆锥曲线的位置关系)和实际问题。
⑤ 通过圆锥曲线的学习,进一步体会数形结合的思想。
(2)曲线与方程
结合已学过的曲线及其方程的实例,了解曲线与方程的对应关系,进一步感受数形结合的基本思想。
1.常用逻辑用语(约8课时)
(1)命题及其关系
① 了解命题的逆命题、否命题与逆否命题。
② 理解必要条件、充分条件与充要条件的意义,会分析四种命题的相互关系。
(2)简单的逻辑联结词
通过数学实例,了解逻辑联结词“或”“且”“非”的含义。
(3)全称量词与存在量词
① 通过生活和数学中的丰富实例,理解全称量词与存在量词的意义。
② 能正确地对含有一个量词的命题进行否定。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com