(二)问题探究

1．几何元素计数问题

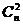例1(1)凸n(n>4)边形的对角线有多少条？对角线最多有几个交点？(-n=;)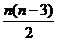

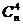(2)平面内有9个点，其中4个点在一条直线上，此外没有3个点在一条直线上，过这9个点可以作 80 个三角形。

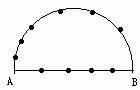
例2．如图，在以AB为直径的半圆上，有异于A、B的6个点C1，C2，…，C6，AB上异于A、B的4个点D1，D2，D3，D4，问：

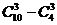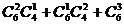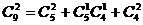以这10个点中的3个占为顶点作三角形可作多少个？其中含C1点有多少个？(==116；=36)

以图中12个点(含A，B)中的4个为顶点，可作出多少个四边形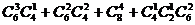？(=360或)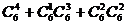

例3．空间12个点，其中5个点共面，此外无任何4个点共面，这12个点可决定多少个平面？(211)

分析：可分四类考虑

①5个共面点决定1个平面；②5个共面点中任何2个点和其余7个点任意一点决定7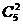；③5个共面点中任何1个点和其余7个点任意两点决定5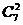；④7个点中任何3个点决定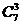。由分类计数原理即可求得。

例4．已知平面α∥β,在内有4个点，在内有6个点

经过3点作一平面，最多可作多少个不同的平面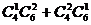？(+2=98)

以这些点为顶点，最多可构成多少个三棱锥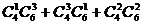？(=194)

上述三棱锥中最多可以有多少个不同的体积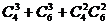？(=114)

2．整数的约数个数问题

例5．求2700(=22×33×52)约数个数？

3．其它计数问题(集合、映射个数等)

例6．(1)(a+b)n展开式共有多少项？每一项的结构特点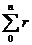？( =n+1, 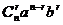,r=0,1,2,…,n)

(2)若A={1,2,3},B={0,-1,1},则使任意x∈A，且x+f(x)是偶数的映射f：A®B的个数是多少？ (9)

分析：x,f(x)应同奇偶，分两大步完成：

第一步：找出x∈A，且x是奇数的象f(x)的选取法有：23；(1，3，5的象可从中选)

第二步：找出x∈A，且x是偶数的象f(x)的选取法有：1；(2，4的象只能取0)

(3)设含有10个元素的集合的全部子集数为S，其中3个元素组成的子集数为T，则T/S=　　 (1992年全国高考题)(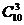/210=15/128)

例7．《教学与测试》P277§71备用题6

(一)计数问题的求解策略及注意事项：

1．求解策略

列举法；

公式法。

2．注意事项：在计数过程中，要防止遗漏和重复！

教学重点：空间、平面、整数中的有关计数问题。

教学难点：空间、平面、整数中的有关计数问题的解法。

解决方法：启发式．

(三)德育渗透点

学生学会用联系的观点看问题，把握空间、平面、整数中的有关计数问题的规律及解法，进一步提高分析问题和解决问题的能力。

(二)能力训练点

探索空间、平面、整数中的有关计数问题规律，掌握其解法。

知识教学点

1．空间、平面、整数中的有关计数问题

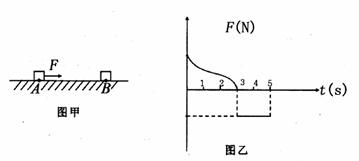
18．(18分)如图甲所示，一质量为m=1kg的小物体静止在粗糙水平面上的A点上，从t=0时刻开始，小物体在水平力F作用下向右运动，水平力F随时间的变化规律如图乙所示。第3s末小物体运动到B点时速度刚好为零，第5秒末小物体刚好回到A点，已知小物体与粗糙水平面间的动摩擦因数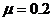，(g取10m/s²)求：

　 (1)AB间的距离；

　 (2)水平力F在5s时间内对小物体所做的功。

17．如图，ABCD为一竖直平面的轨道，其中BC水平，A点比BC高出10米，BC长1米，AB和CD轨道光滑。一质量为1千克的物体，从A点以4米/秒的速度开始运动，经过BC后滑到高出C点10.3m的D点速度为零。求：(g=10m/s²)

　 (1)物体与BC轨道的滑动摩擦系数。

　 (2)物体第5次经过B点的速度。

　 (3)物体最后停止的位置(距B点)。

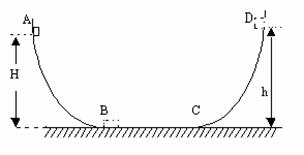　 　 (4)物体一共经过C点多少次？

16．(10分)蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目．一个质量为 60 kg的运动员，从离水平同面3.2m处自由下落，着网后沿竖直方向蹦回到离水平网面5.0m高处．已知运动员与网接触的时间为1.2s．若把在这段时间内网对运动员的作用力当作恒力处理，求此力的大小．(g=10 m/s²)(2002年全国高考题)

14．(12分)质量为3000t的列车，在恒定的额定功率下，由静止开始出发，运动过程中受到的阻力大小恒定，经过10³s速度达到最大行驶速度72km/h。此时司机发现前方4km处的铁轨被洪水冲毁，便立即紧急刹车，结果列车正好到达铁轨冲毁处停止，若所加的制动力为7.5×10⁴N。求：

　 (1)列车在行驶过程中所受阻力多大？

　 (2)列车的额定功率多大？

　 (3)列车的总行程多长？

15：电动机通过一绳吊起一质量为m=8kg的物体，绳的最大拉力为F_m=120N，电动机的最大输出功率为P_m=1200W，要将此物体由静止开始以最快的方式吊起H=90m，(已知此物体在被吊高90m时已开始以最大的速度匀速上升)，所需的时间为多少(空气阻力不计)。