
例8.对于函数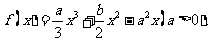
(1)若函数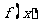 在
在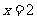 处的切线方程为
处的切线方程为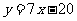 ,求
,求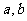 的值;
的值;
(2)设 是函数
是函数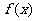 的两个极值点,且
的两个极值点,且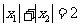 ,证明:
,证明: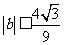
变式:
已知函数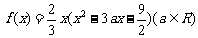
(1)若函数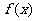 图像上点
图像上点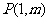 处的切线方程为
处的切线方程为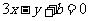 ,求
,求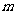 的值.
的值.
(2)若函数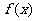 在
在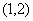 内是增函数,且
内是增函数,且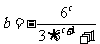 (
(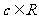 ),试比较
),试比较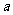 与
与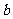 的大小.
的大小.
反馈练习:
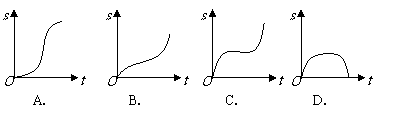
1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程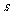 看作时间
看作时间 的函数,其图像可能是( )
的函数,其图像可能是( )

例7.已知函数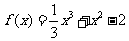
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点 (n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值。
例6.已知函数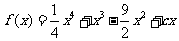 有三个极值点。
有三个极值点。
(1)证明: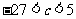 ;
;
(2)若存在实数c,使函数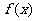 在区间
在区间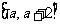 上单调递减,求
上单调递减,求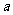 的取值范围。
的取值范围。
变式:
已知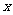 =3是函数
=3是函数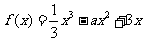 的一个极值点。
的一个极值点。
(1)求函数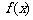 的单调区间;
的单调区间;
(2)若直线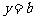 与函数
与函数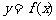 的图象有3个交点,求
的图象有3个交点,求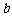 的取值范围。
的取值范围。
例4.设函数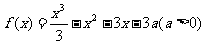 。
。
(1) 如果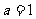 ,点
,点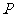 为曲线
为曲线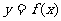 上一个动点,求以
上一个动点,求以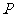 为切点的切线斜率取最小值时的切线方程;
为切点的切线斜率取最小值时的切线方程;
(2) 若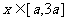 时,
时,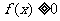 恒成立,求
恒成立,求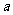 的取值范围。
的取值范围。
例5.函数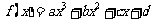 在
在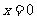 处取得极值,曲线
处取得极值,曲线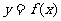 过原点和点P(-1,2),若曲线
过原点和点P(-1,2),若曲线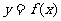 在P处的切线
在P处的切线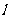 与直线
与直线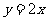 的夹角为
的夹角为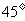 ,且
,且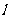 的倾斜角为钝角.
的倾斜角为钝角.
(1)求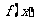 的解析式;
的解析式;
(2)若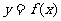 在区间
在区间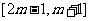 上是增函数,求实数
上是增函数,求实数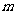 的取值范围;
的取值范围;
(3)若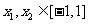 ,求证:
,求证: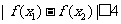 .
.
变式:
设函数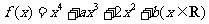 ,其中
,其中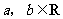 .
.
(1)当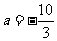 时,讨论函数
时,讨论函数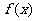 的单调性;
的单调性;
(2)若函数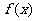 仅在
仅在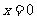 处有极值,求
处有极值,求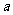 的取值范围;
的取值范围;
(3)若对于任意的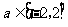 ,不等式
,不等式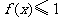 在
在 上恒成立,求
上恒成立,求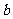 的取值范围.
的取值范围.
例3.用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
变式:
某公司为获更大收益,每年要投入一定资金用于广告促销,经调查,若每年投广告费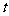 (百万元),可增加销售额约为
(百万元),可增加销售额约为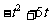 (百万元).
(百万元). 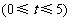 .
.
(1)若公司将当年的广告费控制在3百万元之内,则应投入多少广告费才能使公司由此获得收益最大?
(2)现公司准备共投入3百万元分别用于广告促销和技术改造,经预测,每投入技术改进费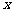 百万元,可增加销售额约
百万元,可增加销售额约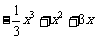 百万元.请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益=销售额-成本)
百万元.请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益=销售额-成本)
例1.已知函数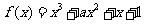 ,
,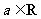 .
.
(1)讨论函数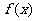 的单调区间;
的单调区间;
(2)设函数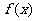 在区间
在区间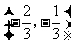 内是减函数,求
内是减函数,求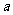 的取值范围.
的取值范围.
例2.已知定义在R上的函数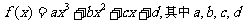 是实数.
是实数.
(1)若函数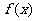 在区间
在区间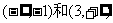 上都是增函数,在区间(-1,3)上是减函数,并且
上都是增函数,在区间(-1,3)上是减函数,并且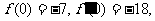 求函数
求函数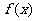 的表达式;
的表达式;
(2)若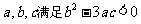 ,求证:函数
,求证:函数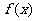 是单调函数.
是单调函数.
变式:
已知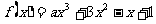 在R上是减函数,求
在R上是减函数,求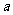 的取值范围。
的取值范围。
函数、导数和不等式这三部分内容都是高考考查的重点,题型既有灵活多变的客观性试题,又有具有一定能力要求的主观性试题。纵观近年的高考试题,对函数的主干知识,函数知识的综合应用,函数与导数、不等式的结合,利用导数研究函数的单调性、求函数的极值和最值等内容是本专题考查的重点,而本专题命题的热点主要是函数的图像与性质,以函数为背景的方程、不等式问题,以函数为模型运用导数解决的应用问题等几个方面。
14.用KMnO4氧化密度为1.19g/cm3,溶质质量为36.5%的 HCl.反应方程式如下:
2KMnO4 + 16HCl = 2KCl + 2MnCl 2+ 5Cl 2↑ + 8H2O
(1)15.8g KMnO4能使多少克HCl发生上述反应?有多少克HCl被氧化?
(2)若Cl 2在标准状况下的密度为3.17g/L,则产生的Cl 2在标准状况下的体积为多少?
13.某溶液中含有Ba2+,Cu2+,Ag+,现用NaOH溶液、
盐酸和Na2SO4溶液将这三种离子逐一沉淀分离。
其流程图如右(写出最佳答案)
(1).沉淀的化学式:沉淀1 ,
沉淀2 ,
沉淀3 ;
(2).写出混合液+A的离子方程式
溶液+B的离子方程式
12.将下列离子Na+、K+、Cu2+、H+、NO3-、Cl-、CO32-、OH-按可能大量共存于同一溶液的情况,把他们分成A、B两组,而且每组中均含两种阳离子和两种阴离子。
A组:
B组:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com