
例8.对于函数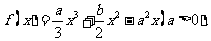
(1)若函数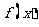 在
在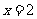 处的切线方程为
处的切线方程为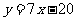 ,求
,求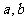 的值;
的值;
(2)设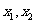 是函数
是函数 的两个极值点,且
的两个极值点,且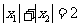 ,证明:
,证明: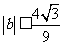
解:(1)由切点为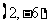 ,
,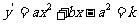 ,有
,有
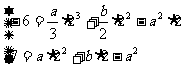 解得
解得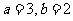
(2)由题,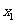 、
、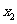 是方程
是方程 的两个根,
的两个根,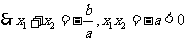 可得两根一正一负,
可得两根一正一负,
不妨设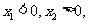
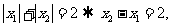
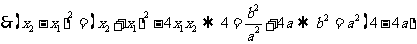 .
.
设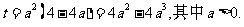
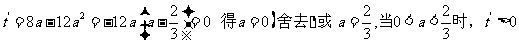 ;
;
当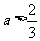 时,
时,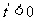 . 所以当
. 所以当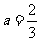 时,
时, ,即
,即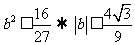 .
.
变式:
已知函数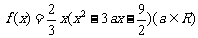
(1)若函数 图像上点
图像上点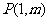 处的切线方程为
处的切线方程为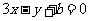 ,求
,求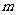 的值.
的值.
(2)若函数 在
在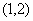 内是增函数,且
内是增函数,且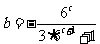 (
(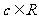 ),试比较
),试比较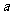 与
与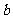 的大小.
的大小.
解:(1)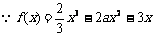
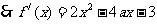 ,则过点
,则过点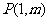 的切线斜率为
的切线斜率为
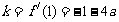 .
. 切线方程为
切线方程为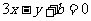 ,
,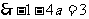 ,即
,即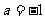 .
.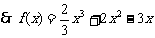 .
.

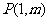 在
在 的图像上,
的图像上,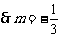 .
.
(2) 函数
函数 在
在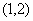 内是增函数,
内是增函数,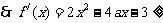 对一切
对一切 恒成立,即
恒成立,即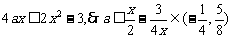 .
. 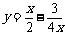 在
在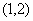 内是增函数,
内是增函数,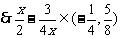 ,
,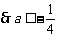 .令
.令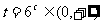 ,则
,则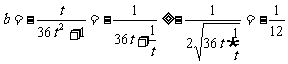 (当且仅当
(当且仅当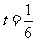 取等号),故
取等号),故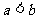 。
。
反馈练习:
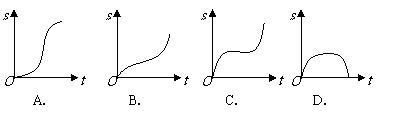
1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程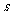 看作时间
看作时间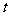 的函数,其图像可能是( A
)
的函数,其图像可能是( A
)

例7.已知函数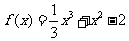 。
。
(1)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点 (n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(2)求函数f(x)在区间(a-1,a)内的极值。
解:(1)因为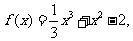 所以
所以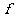 ′(x)=x2+2x,由点
′(x)=x2+2x,由点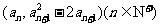 在函数y=f′(x)的图象上,又
在函数y=f′(x)的图象上,又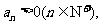 所以
所以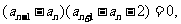
所以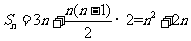 ,又因为
,又因为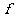 ′(n)=n2+2n,所以
′(n)=n2+2n,所以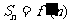 ,
,
故点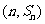 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(2) 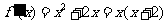 ,由
,由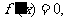 得
得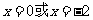 .当x变化时,
.当x变化时,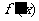 ﹑
﹑ 的变化情况
的变化情况
|
x |
(-∞,-2) |
-2 |
(-2,0) |
0 |
(0,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
注意到 ,从而
,从而
①当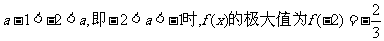 ,此时
,此时 无极小值;
无极小值;
②当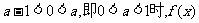 的极小值为
的极小值为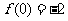 ,此时
,此时 无极大值;
无极大值;
③当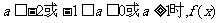 既无极大值又无极小值.
既无极大值又无极小值.
例6.已知函数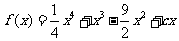 有三个极值点。
有三个极值点。
(1)证明: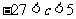 ;
;
(2)若存在实数c,使函数 在区间
在区间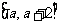 上单调递减,求
上单调递减,求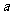 的取值范围。
的取值范围。
解:(1)因为函数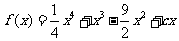 有三个极值点, 所以
有三个极值点, 所以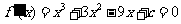 有三个互异的实根.设
有三个互异的实根.设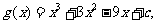 则
则
当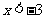 时,
时,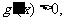
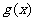 在
在 上为增函数;当
上为增函数;当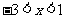 时,
时,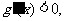
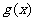 在
在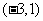 上为减函数;当
上为减函数;当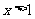 时,
时,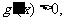
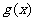 在
在 上为增函数,
上为增函数,
所以函数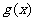 在
在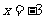 时取极大值,在
时取极大值,在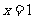 时取极小值。
时取极小值。
当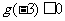 或
或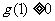 时,
时,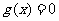 最多只有两个不同实根。
最多只有两个不同实根。
因为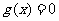 有三个不同实根, 所以
有三个不同实根, 所以 且
且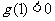 ,
,
即 ,且
,且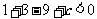 ,解得
,解得 且
且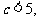 故
故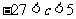 .
.
(2)由(1)的证明可知,当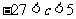 时,
时,  有三个极值点.
有三个极值点.
不妨设为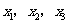 (
(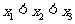 ),则
),则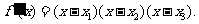
所以 的单调递减区间是
的单调递减区间是 ,
,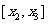
若 在区间
在区间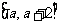 上单调递减,则
上单调递减,则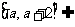
 , 或
, 或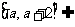
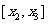 ,
,
若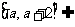
 ,则
,则 .由(I)知,
.由(I)知,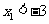 ,于是
,于是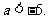
若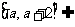
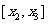 ,则
,则 且
且 .由(I)知,
.由(I)知,
又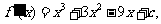 当
当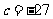 时,
时,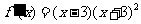 ;
;
当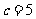 时,
时,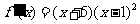 .因此, 当
.因此, 当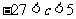 时,所以
时,所以 且
且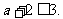
即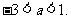 故
故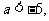 或
或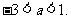 反之, 当
反之, 当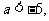 或
或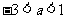 时,总可找到
时,总可找到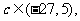 使函数
使函数 在区间
在区间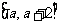 上单调递减。综上所述,
上单调递减。综上所述, 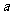 的取值范围是
的取值范围是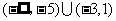 .
.
变式:
已知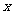 =3是函数
=3是函数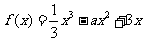 的一个极值点。
的一个极值点。
(1)求函数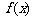 的单调区间;
的单调区间;
(2)若直线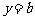 与函数
与函数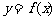 的图象有3个交点,求
的图象有3个交点,求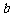 的取值范围。
的取值范围。
解:(1)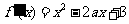
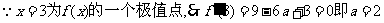
有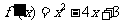 令
令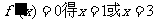
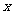 |
 |
1 |
(1,3) |
3 |
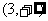 |
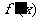 |
+ |
0 |
- |
0 |
+ |
 |
 |
极大值 |
 |
极小值 |
 |
∴由上表可知, 的单调递增区间为
的单调递增区间为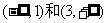 ,其单调减区间为(1,3)
,其单调减区间为(1,3)
(2)由(1)知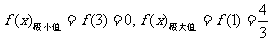 ,若直线
,若直线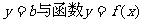 的图象有3个交点则
的图象有3个交点则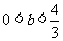 。
。
例4.设函数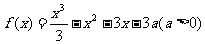 。
。
(1) 如果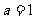 ,点
,点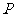 为曲线
为曲线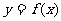 上一个动点,求以
上一个动点,求以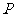 为切点的切线斜率取最小值时的切线方程;
为切点的切线斜率取最小值时的切线方程;
(2) 若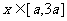 时,
时,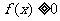 恒成立,求
恒成立,求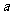 的取值范围。
的取值范围。
解:(1) 设切线斜率为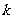 ,则
,则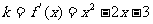 当
当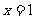 时,
时,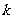 取最小值-4,
取最小值-4,
又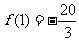 , 所以,所求切线方程为
, 所以,所求切线方程为 ,即
,即 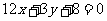
(2)
由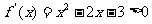 ,解得:
,解得: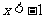 或
或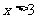 。
。
函数 在
在 和
和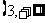 上是增函数,在
上是增函数,在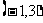 上是减函数。
上是减函数。
所以 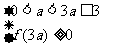 或
或 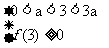 或
或 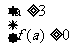 解得
解得 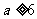
故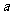 的取值范围是
的取值范围是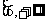 。
。
例5.已知函数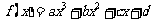 在
在 处取得极值,曲线
处取得极值,曲线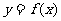 过原点和点P(-1,2),若曲线
过原点和点P(-1,2),若曲线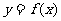 在P处的切线
在P处的切线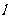 与直线
与直线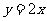 的夹角为
的夹角为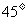 ,且
,且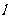 的倾斜角为钝角.
的倾斜角为钝角.
(1)求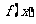 的解析式;
的解析式;
(2)若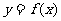 在区间
在区间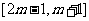 上是增函数,求实数
上是增函数,求实数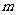 的取值范围;
的取值范围;
(3)若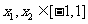 ,求证:
,求证: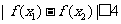 .
.
解:(1) 曲线
曲线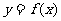 过原点,
过原点,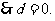

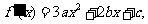 且
且 是
是 的极值点,
的极值点,
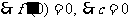 ,
, 过点P(-1,2)的切线
过点P(-1,2)的切线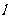 的斜率为
的斜率为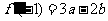 ,
,
由夹角公式得: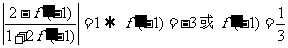
 切线
切线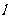 的倾斜角为钝角,
的倾斜角为钝角,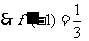 舍去.
舍去.
由
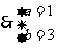 故
故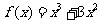
(2)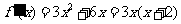 ,令
,令 即
即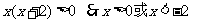
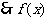 的增区间为
的增区间为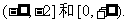
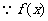 在区间
在区间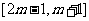 上是增函数,
上是增函数,
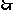
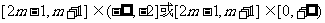 ;
;
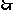

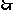
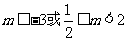
(3)令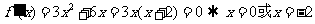 ,
,
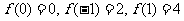 ,
,
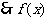 在区间[-1,1]上的最大值M为4,最小值N为0,
在区间[-1,1]上的最大值M为4,最小值N为0,
故对任意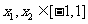 ,有
,有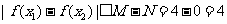
变式:
设函数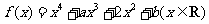 ,其中
,其中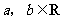 .
.
(1)当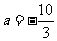 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若函数 仅在
仅在 处有极值,求
处有极值,求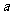 的取值范围;
的取值范围;
(3)若对于任意的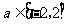 ,不等式
,不等式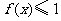 在
在 上恒成立,求
上恒成立,求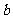 的取值范围.
的取值范围.
解:(1)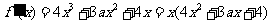 .
.
当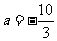 时,
时,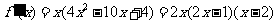 .
.
令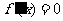 ,解得
,解得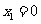 ,
,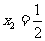 ,
,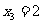 .当
.当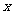 变化时,
变化时,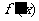 ,
, 的变化情况如下表:
的变化情况如下表:
 |
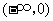 |
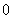 |
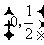 |
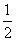 |
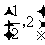 |
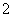 |
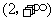 |
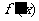 |
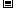 |
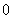 |
 |
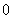 |
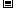 |
 |
 |
 |
↘ |
极小值 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以 在
在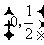 ,
,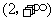 内是增函数,在
内是增函数,在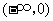 ,
,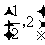 内是减函数.
内是减函数.
(2)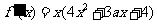 ,显然
,显然 不是方程
不是方程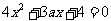 的根.
的根.
为使 仅在
仅在 处有极值,必须
处有极值,必须 恒成立,即有
恒成立,即有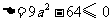 .
.
解此不等式,得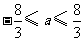 .这时,
.这时,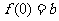 是唯一极值.因此满足条件的
是唯一极值.因此满足条件的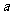 的取值范围是
的取值范围是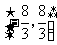 .
.
(3)由条件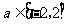 可知
可知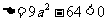 ,从而
,从而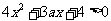 恒成立.
恒成立.
当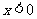 时,
时,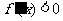 ;当
;当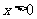 时,
时, .
.
因此函数 在
在 上的最大值是
上的最大值是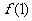 与
与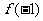 两者中的较大者.
两者中的较大者.
为使对任意的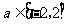 ,不等式
,不等式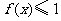 在
在 上恒成立,当且仅当
上恒成立,当且仅当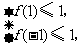 即
即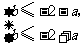 在
在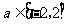 上恒成立.所以
上恒成立.所以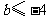 ,因此满足条件的
,因此满足条件的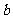 的取值范围是
的取值范围是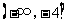 .
.
例3.用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
解:设长方体的宽为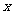 (m),则长为
(m),则长为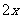 (m),高为
(m),高为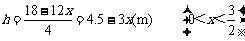 .
.
故长方体的体积为
从而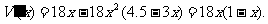 令
令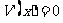 ,解得
,解得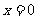 (舍去)或
(舍去)或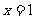 ,因此
,因此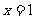 .
.
当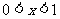 时,
时,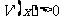 ;当
;当 时,
时,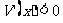 ,故在
,故在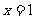 处
处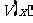 取得极大值,并且这个极大值就是
取得极大值,并且这个极大值就是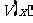 的最大值,从而最大体积
的最大值,从而最大体积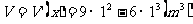 ,此时长方体的长为2 m,高为1.5
m
,此时长方体的长为2 m,高为1.5
m
变式:
某公司为获更大收益,每年要投入一定资金用于广告促销,经调查,若每年投广告费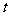 (百万元),可增加销售额约为
(百万元),可增加销售额约为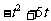 (百万元).
(百万元). 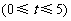 .
.
(1)若公司将当年的广告费控制在3百万元之内,则应投入多少广告费才能使公司由此获得收益最大?
(2)现公司准备共投入3百万元分别用于广告促销和技术改造,经预测,每投入技术改进费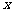 百万元,可增加销售额约
百万元,可增加销售额约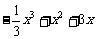 百万元.请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益=销售额-成本)
百万元.请设计一种资金分配方案,使该公司由此获得最大收益.(注:收益=销售额-成本)
解:(1)设投入广告费t百万元,则收益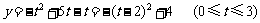 。
。
∴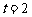 时,
时,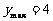 .∴应投入2百万元广告费,由此获得收益最大。
.∴应投入2百万元广告费,由此获得收益最大。
(2)投入广告费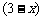 百万元,则收益
百万元,则收益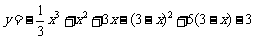
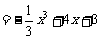
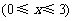
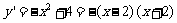
当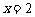 时,
时,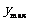 . ∴当投入技术改造2百万元、广告费1百万元时,公司收益最大。
. ∴当投入技术改造2百万元、广告费1百万元时,公司收益最大。
例1.已知函数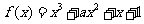 ,
,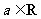 .
.
(1)讨论函数 的单调区间;(2)设函数
的单调区间;(2)设函数 在区间
在区间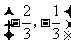 内是减函数,求
内是减函数,求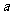 的取值范围.
的取值范围.
解:(1)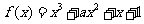 求导得
求导得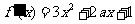
当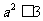 时,
时,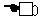 ,
, ,
, 在
在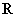 上递增;
上递增;
当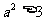 ,
,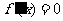 求得两根为
求得两根为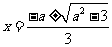 ,
,
即 在
在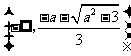 递增,
递增,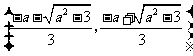 递减,
递减, 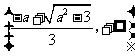 递增。
递增。
(2)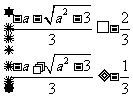 ,且
,且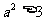 ,解得
,解得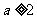 。
。
例2.已知定义在R上的函数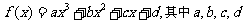 是实数.
是实数.
(1)若函数 在区间
在区间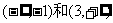 上都是增函数,在区间(-1,3)上是减函数,并且
上都是增函数,在区间(-1,3)上是减函数,并且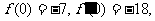 求函数
求函数 的表达式;
的表达式;
(2)若 ,求证:函数
,求证:函数 是单调函数.
是单调函数.
解:(1)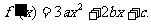 由
由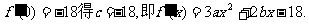
又由于 在区间
在区间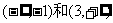 上是增函数,在区间(-1,3)上是减函数,所以
上是增函数,在区间(-1,3)上是减函数,所以
-1和3必是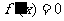 的两个根,从而
的两个根,从而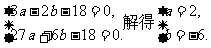
又根据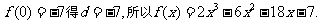
(2)因为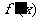 为二次三项式,并且
为二次三项式,并且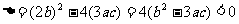 ,当
,当 恒成立,此时函数
恒成立,此时函数 是单调递增函数;当
是单调递增函数;当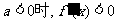 恒成立,此时函数
恒成立,此时函数 是单调递减函数,因此对任意给定的实数a,函数
是单调递减函数,因此对任意给定的实数a,函数 总是单调函数。
总是单调函数。
变式:
已知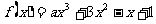 在R上是减函数,求
在R上是减函数,求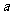 的取值范围。
的取值范围。
解:函数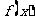 的导数为
的导数为 。对于
。对于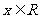 都有
都有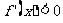 时,
时,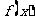 为减函数。由
为减函数。由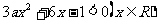 可得
可得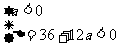 ,解得
,解得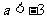 。
。
当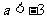 时函数
时函数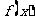 在R上是减函数;当
在R上是减函数;当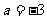 时,
时,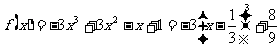 ,由函数
,由函数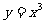 在R上的单调性,可知当
在R上的单调性,可知当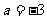 时函数
时函数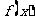 在R上是减函数;当
在R上是减函数;当 时函数
时函数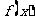 在R上存在增区间。综上
在R上存在增区间。综上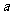 的取值范围是
的取值范围是 。
。
函数、导数和不等式这三部分内容都是高考考查的重点,题型既有灵活多变的客观性试题,又有具有一定能力要求的主观性试题。纵观近年的高考试题,对函数的主干知识,函数知识的综合应用,函数与导数、不等式的结合,利用导数研究函数的单调性、求函数的极值和最值等内容是本专题考查的重点,而本专题命题的热点主要是函数的图像与性质,以函数为背景的方程、不等式问题,以函数为模型运用导数解决的应用问题等几个方面。
14.设函数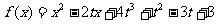 ,
,
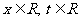 ,
将
,
将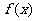 的最小值记为
的最小值记为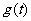 .
.
(1)求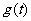 的表达式;
的表达式;
(2)讨论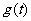 在区间[-1,1]内的单调性;
在区间[-1,1]内的单调性;
(3) 若当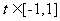 时,
时,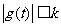 恒成立,其中
恒成立,其中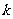 为正数,求
为正数,求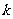 的取值范围.
的取值范围.
13.已知函数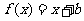 的图像与函数
的图像与函数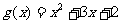 的图象相切,记
的图象相切,记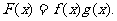
(1)求实数b的值及函数F(x)的极值;
(2)若关于x的方程F(x)= k恰有三个不等的实数根,求实数k的取值范围.
12.已知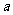 为实数,函数
为实数,函数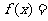
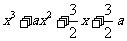 .
.
(1)若函数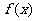 的图象上有与
的图象上有与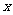 轴平行的切线,求
轴平行的切线,求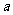 的取值范围;
的取值范围;
(2)若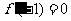 ,对任意
,对任意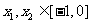 ,不等式
,不等式 恒成立,求
恒成立,求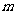 的最小值.
的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com