
|
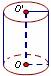
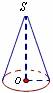
图形 |
 |
 |
|
|
|
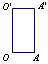
定义 |
 |
 |
|
|
|
有关线 |
轴 |
直线 |
直线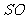 |
|
|
母线 |
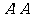 |
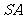 |
|
|
|
有关面 |
底面 |
圆 |
圆 |
|
|
平行于底 的截面 |
圆 |
圆 |
|
|
|
轴截面 |
全等的矩形 |
全等的等腰三角形 |
|
|
|
侧面及 展开图 |
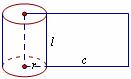 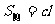 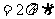 |
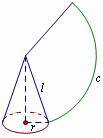 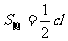  |
|
|
|
|
|
|
|
|
|
|
|
|
|
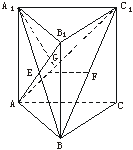
10. 在直三棱柱ABC-A1B1C1中,AB1⊥BC1,AB=CC1=a,BC=b.
(1)设E、F分别为AB1、BC1的中点,求证:EF∥平面ABC;
(2)求证:A1C1⊥AB;
(3)求点B1到平面ABC1的距离.
(1)证明:∵E、F分别为AB1、BC1的中点,
∴EF∥A1C1.∵A1C1∥AC,∴EF∥AC.
∴EF∥平面ABC.
(2)证明:∵AB=CC1,
∴AB=BB1.又三棱柱为直三棱柱,
∴四边形ABB1A1为正方形.连结A1B,则A1B⊥AB1.
又∵AB1⊥BC1,
∴AB1⊥平面A1BC1. ∴AB1⊥A1C1.
又A1C1⊥AA1,
∴A1C1⊥平面A1ABB1. ∴A1C1⊥AB.
(3)解:∵A1B1∥AB,∴A1B1∥平面ABC1.
∴A1到平面ABC1的距离等于B1到平面ABC1的距离.过A1作A1G⊥AC1于点G,
∵AB⊥平面ACC1A1,
∴AB⊥A1G.从而A1G⊥平面ABC1,故A1G即为所求的距离,即A1G=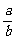
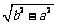 .
.
评述:本题(3)也可用等体积变换法求解.
[探索题](2004年春季上海)如下图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EFcos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
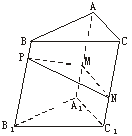
(1)证明:∵CC1∥BB1 CC1⊥PM,CC1⊥PN,
CC1⊥PM,CC1⊥PN,
∴CC1⊥平面PMN CC1⊥MN.
CC1⊥MN.
(2)解:S2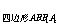 =S2
=S2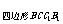 +S2
+S2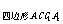 -2S
-2S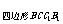 ·S
·S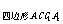 cosα,
cosα,
其中α为平面CC1B1B与平面CC1A1A所成的二面角.
∵CC1⊥平面PMN,∴上述的二面角为∠MNP.
在△PMN中,
PM2=PN2+MN2-2PN.MNcos∠MNP
 PM2CC12=PN2CC12+MN2CC12
PM2CC12=PN2CC12+MN2CC12
-2(PN·CC1)·(MN·CC1)cos∠MNP.
∵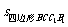 =PN·CC1,
=PN·CC1,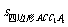 =MN·CC1,
=MN·CC1,
S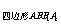 =PM·BB1,
=PM·BB1,
∴S2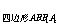 =S2
=S2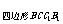 +S2
+S2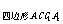 -
-
2S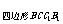 ·S
·S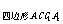 cosα
cosα
9.正方形ABCD中,AB=2,E是AB边的中点,F是BC边上一点,将△AED及△DCF折起(如下图),使A、C点重合于A′点.
(1)证明:A′D⊥EF;
(2)当F为BC的中点时,求A′D与平面DEF所成的角;
(3)当BF=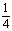 BC时,求三棱锥A′-EFD的体积.
BC时,求三棱锥A′-EFD的体积.

(1)证明:略
(2)解:取EF的中点G,连结A′G、DG…………
平面DEF⊥平面A′DG.
作A′H⊥DG于H,得A′H⊥平面DEF,
∴∠A′DG为A′D与平面DEF所成的角.
在Rt△A′DG中,A′G=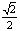 ,
,
A′D=2, ∴∠A′DG=arctan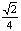 .
.
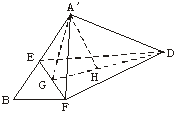
(3)解:∵A′D⊥平面A′EF,
∴A′D是三棱锥D-A′EF的高.
又由BE=1,BF=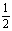 推出EF=
推出EF=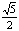 ,可得S
,可得S =
=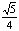 ,
,
VA′-EFD=VD-A′EF=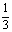 ·S
·S ·A′D
·A′D
=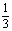 ·
·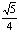 ·2=
·2=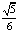 .
.
8.(2006福建) 如图,四面体ABCD中,O、E分别是BD、BC的中点,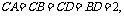
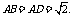
(I)求证: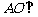 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
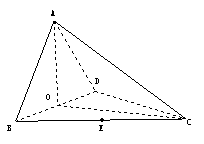 (III)求点E到平面ACD的距离.
(III)求点E到平面ACD的距离.
解法一:
(I)证明:证∠AOB=900.
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知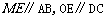
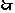 直线OE与EM所成的锐角就是异面直线AB与CD所成的角. 在
直线OE与EM所成的锐角就是异面直线AB与CD所成的角. 在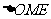 中,
中,
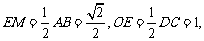
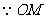 是直角
是直角 斜边AC上的中线,
斜边AC上的中线,
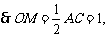
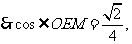
AB与CD所成角的大小为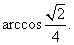
(III)等积法得
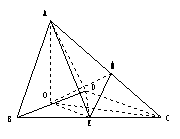
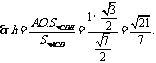
即为所求.
7.如图ABCD是矩形,PA^平面ABCD,DPAD是等腰三角形,M、N分别是AB、PC的中点,求证:MN^平面PCD
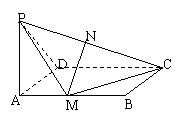 证略
证略
6. AC⊥BD或四边形ABCD菱形等;
[解答题]
6. 在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件_______时,有A1C⊥B1D1 (注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况)
◆答案提示: 1-4 CDAC; 5.3cm;
5.△ABC的三个顶点A、B、C到平面α的距离分别为2 cm、3 cm、4 cm,且它们在α的同侧,则△ABC的重心到平面α的距离为______
4.PA垂直于以AB为直径的圆所在的平面,C为圆上异于A、B的任一点,则下列关系不正确的是 ( )
A PA⊥BC B BC⊥平面PAC C AC⊥PB D PC⊥BC
[填空题]
3.给出下列命题:
①若平面α的两条斜线段PA、PB在α内的射影长相等,那么PA、PB的长度相等;
②已知PO是平面α的斜线段,AO是PO在平面α内的射影,若OQ⊥OP,则必有OQ⊥OA;
③与两条异面直线都平行的平面有且只有一个;
④平面α内有两条直线a、b都与另一个平面β平行,则α∥β.
上述命题中不正确的是 ( )
A.①②③④ B.①②③ C.①③④ D.②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com