5．下列各项中最适合填在横线上的一项是

(　)

尊严的具体性不只表现在工作有岗位、生活有保障上，更表现在你可以自由、独立地存在，不会依附于强权，可以建立并实现你的自我价值。这样，________。

A．每个国民才是有尊严的国民，无数个有尊严的国民构成的国家才是真正有尊严的国家，才会真正赢得世界的尊重与敬重

B．国家才是有尊严的国家，每个国民才是有尊严的国民，才会真正赢得世界的尊重与敬重

C．才会赢得世界的尊重与敬重，才使每个国民成为有尊严的国民，国家才是真正有尊严的国家

D．每个国民才是有尊严的国民，才会真正赢得世界的尊重与敬重，国家才会由无数个有尊严的国民构成真正有尊严的国家

[解析]　注意说话的顺序，一般的顺序是由小到大，由国民的尊严到国家的尊严，再到国家受到尊重与敬重。

[答案]　A

4．把下列句子组合成语意连贯的一段话，填写在横线上，组合恰当的一组是

(　)

__________，__________，__________。__________，________，至今成为梅派的必修课程，也成为梅派京剧里美丽动人的形姿。

①创新了旦角的表现力

②也被梅兰芳演变出了五十三种之多

③梅兰芳摸索出了丰富多样的表演技巧

④就算是最简单的旦角手姿

⑤随着改良创新在众多剧目中的实践

A．⑤③①④②　 　　　　　　　　　　　 B．⑤③④②①

C．④②⑤③①　 　　　　　　　　　　　 D．②①⑤④③

[解析]　按照先概述后具体的逻辑顺序排列。⑤③①概括说明梅兰芳在旦角上的创新，④②具体说明他在旦角手姿上的创新。

[答案]　A

1．依次填入下面一段文字横线处的语句，衔接最恰当的一组是

(　)

没有一个人的生命是完整无缺的，每个人都少了一样东西。______________，仿佛我们背上的一根刺，时时提醒我们要谦卑；要懂得怜恤。

①以前我也痛恨我人生中的缺失　②你不想要它　③每个人的生命，都被上苍划上了一道缺口　④因为我认识到生命中的缺口　⑤它却如影随形　⑥但现在我却能宽心接受

A．③②⑤①⑥④　　　　　 B．③②①⑥④⑤

C．①⑥④③②⑤　 　　　　　　　　　 D．①⑥②⑤④③

[解析]　解答此题，首先要注意题中横线前后的语句，由横线前的语句，可确定③紧承其后，由横线后的语句，可确定④在其前，由上述两点即可确定答案。

[答案]　A

12.下面是一个电子元件在处理数据时的流程图：　　　　　　　　　　　　　　 　　　　　　　　

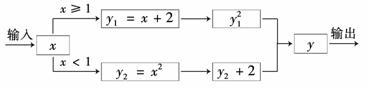
(1)试确定y与x的函数关系式；

(2)求f(－3)、f(1)的值；

(3)若f(x)＝16，求x的值.

解：(1)y＝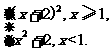

(2)f(－3)＝(－3)²+2＝11；f(1)＝(1+2)²＝9.

(3)若x≥1，则(x+2)²＝16，

解得x＝2或x＝－6(舍)；

若x＜1，则x²+2＝16，

解得x＝(舍)或x＝－.

即x＝2或x＝－.

11.如果f(a+b)＝f(a)·f(b)，且f(1)＝2，则+++…+++＝　　.

解析：f(2)＝f(1)f(1)＝2²，＝2，

f(3)＝f(1)f(2)＝2³，f(4)＝f(2)f(2)＝2⁴，

＝2，…＝2，

∴原式＝2×1005＝2010.

答案：2010

10.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s看作时间t的函数，其图象可能是　　　　　　　　　　　　　　　 (　)

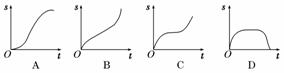
解析：画出曲线的切线，其切线的斜率的意义为速度.由图中切线斜率的变化规律可知选A.

答案：A

9.已知f(x)＝且f(a)＝3，求a的值.

解：①当a≤－1时，f(a)＝a+2，

由a+2＝3，得a＝1，与a≤－1相矛盾，应舍去.

②当－1<a<2时，f (a)＝2 a，

由2a＝3，得a＝，满足－1<a<2.

③当a≥2时，f (a)＝，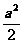

由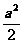＝3，得a＝±，又a≥2，∴a＝.

综上可知，a的值为或.

8.已知函数f(x)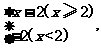＝则不等式x·f(x－1)＜10的解集是　　.

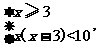解析：当x－1≥2，即x≥3时，不等式等价于解得3≤x＜5；当

x－1＜2，即x＜3时，不等式等价于 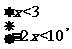解得－5＜x＜3.

综上可知不等式的解集为{x|－5＜x＜5}.

答案：{x|－5＜x＜5}