
5.(08贵州贵阳)25.(本题满分12分)(本题暂无答案)
某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加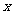 元.求:
元.求:
(1)房间每天的入住量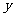 (间)关于
(间)关于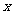 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(2)该宾馆每天的房间收费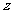 (元)关于
(元)关于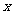 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(3)该宾馆客房部每天的利润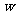 (元)关于
(元)关于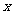 (元)的函数关系式;当每个房间的定价为每天多少元时,
(元)的函数关系式;当每个房间的定价为每天多少元时,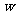 有最大值?最大值是多少?(6分)
有最大值?最大值是多少?(6分)
4. (08广东深圳)22.如图9,在平面直角坐标系中,二次函数
(08广东深圳)22.如图9,在平面直角坐标系中,二次函数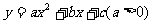 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=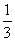 .
(1)求这个二次函数的表达式.
.
(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
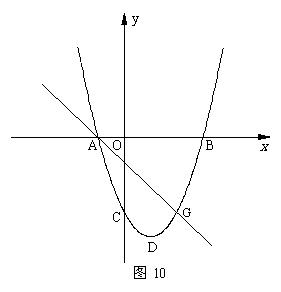
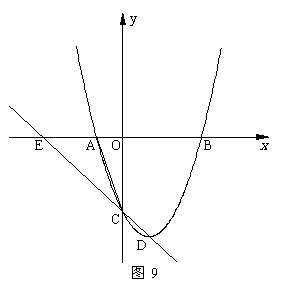 (4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
(4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
(08广东深圳22题解析)22.(1)方法一:由已知得:C(0,-3),A(-1,0) …1分
将A、B、C三点的坐标代入得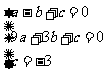 ……………………2分
……………………2分
解得: ……………………3分
……………………3分
所以这个二次函数的表达式为: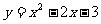 ……………………3分
……………………3分
方法二:由已知得:C(0,-3),A(-1,0) ………………………1分
设该表达式为: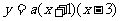 ……………………2分
……………………2分
将C点的坐标代入得: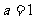 ……………………3分
……………………3分
所以这个二次函数的表达式为: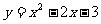 ……………………3分
……………………3分
(注:表达式的最终结果用三种形式中的任一种都不扣分)
(2)方法一:存在,F点的坐标为(2,-3) ……………………4分
理由:易得D(1,-4),所以直线CD的解析式为: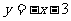
∴E点的坐标为(-3,0) ……………………4分
由A、C、E、F四点的坐标得:AE=CF=2,AE∥CF
∴以A、C、E、F为顶点的四边形为平行四边形
∴存在点F,坐标为(2,-3) ……………………5分
方法二:易得D(1,-4),所以直线CD的解析式为: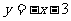
∴E点的坐标为(-3,0) ………………………4分
∵以A、C、E、F为顶点的四边形为平行四边形
∴F点的坐标为(2,-3)或(―2,―3)或(-4,3) 代入抛物线的表达式检验,只有(2,-3)符合∴存在点F,坐标为(2,-3) ………………………5分
 (3)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
(3)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
代入抛物线的表达式,解得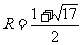 …………6分
…………6分
②当直线MN在x轴下方时,设圆的半径为r(r>0),
则N(r+1,-r),
代入抛物线的表达式,解得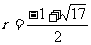 ………7分
………7分
∴圆的半径为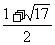 或
或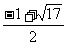 . ……………7分
. ……………7分
(4)过点P作y轴的平行线与AG交于点Q,
易得G(2,-3),直线AG为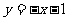 .……………8分
.……………8分
设P(x,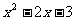 ),则Q(x,-x-1),PQ
),则Q(x,-x-1),PQ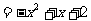 .
.
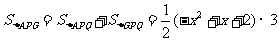 ……………………9分
……………………9分
当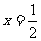 时,△APG的面积最大
时,△APG的面积最大
此时P点的坐标为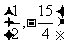 ,
, .
……………………10分
.
……………………10分
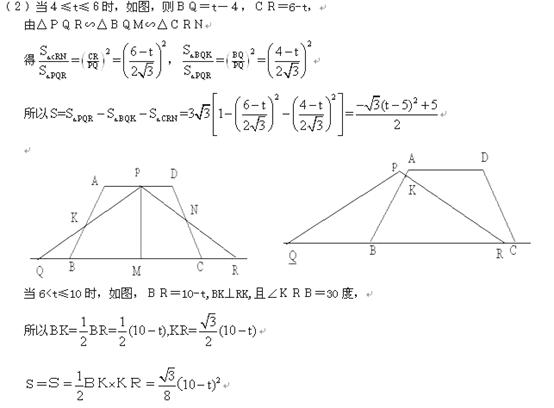
3.(08广东广州)25、(2008广州)(14分)如图11,在梯形ABCD中,AD∥BC,AB=AD=DC=2cm,BC=4cm,在等腰△PQR中,∠QPR=120°,底边QR=6cm,点B、C、Q、R在同一直线l上,且C、Q两点重合,如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动,t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米
(1)当t=4时,求S的值
(2)当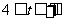 ,求S与t的函数关系式,并求出S的最大值
,求S与t的函数关系式,并求出S的最大值
|
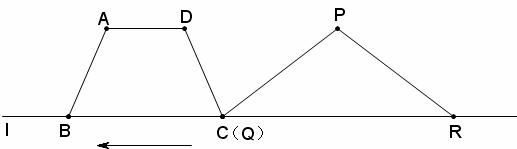
(08广东广州25题解析)25.(1)t=4时,Q与B重合,P与D重合,
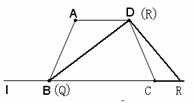 重合部分是
重合部分是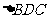 =
=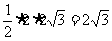
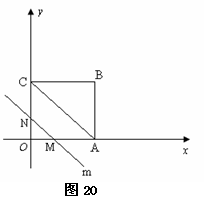
2.(08甘肃白银等9市)28.(12分)如图20,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
(1) 点A的坐标是__________,点C的坐标是__________;
(2) 当t= 秒或
秒时,MN=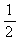 AC;
AC;
(3) 设△OMN的面积为S,求S与t的函数关系式;
(4) 探求(3)中得到的函数S有没有最大值?若有,求出最大值;若没有,要说明理由.
(08甘肃白银等9市28题解析)28. 本小题满分12分
解:(1)(4,0),(0,3); ·················································································· 2分
(2) 2,6; ········································································································· 4分
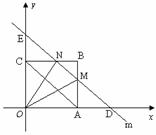 (3) 当0<t≤4时,OM=t.
(3) 当0<t≤4时,OM=t.
由△OMN∽△OAC,得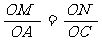 ,
,
∴ ON=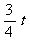 ,S=
,S=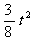 . ···································· 6分
. ···································· 6分
当4<t<8时,
如图,∵ OD=t,∴ AD= t-4.
方法一:
由△DAM∽△AOC,可得AM=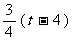 ,∴ BM=6-
,∴ BM=6-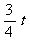 . ···························· 7分
. ···························· 7分
由△BMN∽△BAC,可得BN=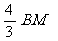 =8-t,∴ CN=t-4. ·································· 8分
=8-t,∴ CN=t-4. ·································· 8分
S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积
=12-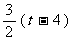 -
-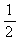 (8-t)(6-
(8-t)(6-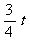 )-
)-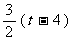
=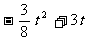 . ··························································································· 10分
. ··························································································· 10分
方法二:
易知四边形ADNC是平行四边形,∴ CN=AD=t-4,BN=8-t.·································· 7分
由△BMN∽△BAC,可得BM=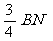 =6-
=6-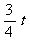 ,∴ AM=
,∴ AM=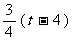 .······ 8分
.······ 8分
以下同方法一.
(4) 有最大值.
方法一:
当0<t≤4时,
∵ 抛物线S=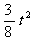 的开口向上,在对称轴t=0的右边, S随t的增大而增大,
的开口向上,在对称轴t=0的右边, S随t的增大而增大,
∴ 当t=4时,S可取到最大值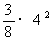 =6; ················ 11分
=6; ················ 11分
当4<t<8时,
∵ 抛物线S=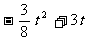 的开口向下,它的顶点是(4,6),∴ S<6.
的开口向下,它的顶点是(4,6),∴ S<6.
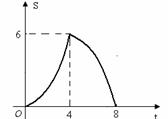 综上,当t=4时,S有最大值6. ······································································· 12分
综上,当t=4时,S有最大值6. ······································································· 12分
方法二:
∵ S=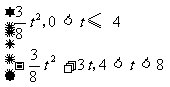
∴ 当0<t<8时,画出S与t的函数关系图像,如图所示. ······························ 11分
显然,当t=4时,S有最大值6. ··································································· 12分
说明:只有当第(3)问解答正确时,第(4)问只回答“有最大值”无其它步骤,可给1分;否则,不给分.
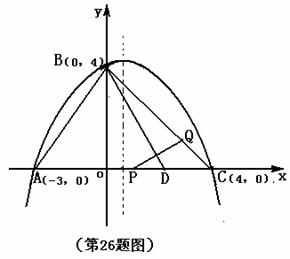
1.(08福建莆田)26.(14分)如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
(1) 求抛物线的解析式.
(2)已知AD = AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t 秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由。
(注:抛物线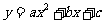 的对称轴为
的对称轴为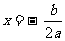 )
)
(08福建莆田26题解析)26(1)解法一:设抛物线的解析式为y = a (x +3 )(x - 4)
因为B(0,4)在抛物线上,所以4 = a ( 0 + 3 ) ( 0 - 4 )解得a= -1/3
所以抛物线解析式为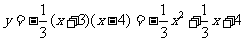
解法二:设抛物线的解析式为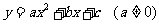 ,
,
依题意得:c=4且 解得
解得
所以 所求的抛物线的解析式为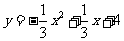
(2)连接DQ,在Rt△AOB中,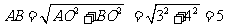
所以AD=AB= 5,AC=AD+CD=3 + 4 = 7,CD = AC - AD = 7 – 5 = 2
因为BD垂直平分PQ,所以PD=QD,PQ⊥BD,所以∠PDB=∠QDB
因为AD=AB,所以∠ABD=∠ADB,∠ABD=∠QDB,所以DQ∥AB
所以∠CQD=∠CBA。∠CDQ=∠CAB,所以△CDQ∽ △CAB
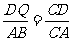 即
即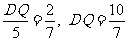
所以AP=AD – DP = AD – DQ=5 –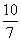 =
=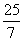 ,
,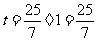
所以t的值是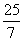
(3)答对称轴上存在一点M,使MQ+MC的值最小
理由:因为抛物线的对称轴为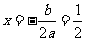
所以A(- 3,0),C(4,0)两点关于直线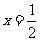 对称
对称
连接AQ交直线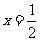 于点M,则MQ+MC的值最小
于点M,则MQ+MC的值最小
过点Q作QE⊥x轴,于E,所以∠QED=∠BOA=900
DQ∥AB,∠ BAO=∠QDE, △DQE ∽△ABO
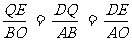 即
即 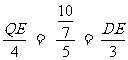
所以QE=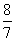 ,DE=
,DE=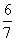 ,所以OE = OD + DE=2+
,所以OE = OD + DE=2+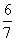 =
=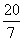 ,所以Q(
,所以Q(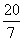 ,
,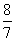 )
)
设直线AQ的解析式为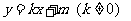
则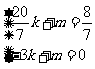 由此得
由此得 
所以直线AQ的解析式为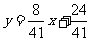 联立
联立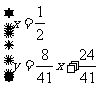
 由此得
由此得 所以M
所以M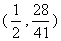
则:在对称轴上存在点M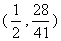 ,使MQ+MC的值最小
,使MQ+MC的值最小
8. 碳、氢、氧3种元素组成的有机物A,相对分子质量为102,含氢的质量分数为9.8%,分子氢原子个数为氧的5倍。
(1)A的分子式是 。
(2)A有2个不同的含氧官能团,其名称是 。
(3)一定条件下,A与氢气反应生成B,B分子的结构可视为1个碳原子上连接2个甲基和另外2个结构相同的基团。
①A的结构简式是 。
②A不能发生的反应是(填写序号字母) 。
a.取代反应 b.消去反应 c.酯化反应 d.还原反应
(4)写出两个与A具有相同官能团、并带有支链的同分异构体的结构简式:
、 。
(5)A还有另一类酯类同分异构体,该异构体在酸性条件下水解,生成两种相对分子质量相同的化合物,其中一种的分子中有2个甲基,此反应的化学方程式是:
7. 2005年的诺贝尔化学奖颁给了3位在烯烃复分解反应研究方面做出突出贡献的化学家。烯烃复分解反应实际上是在金属烯烃络合物的催化下实现C=C双键两边基团换位的反应。如下图表示了两个丙烯分子进行烯烃换位,生成两个新的烯烃分子--丁烯和乙烯。
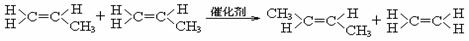
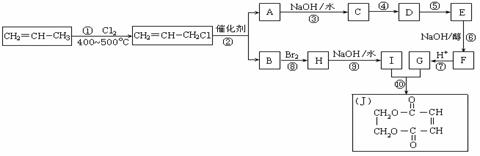
现以石油裂解得到的丙烯为原料,经过下列反应可以分别合成重要的化工原料I和G。I和G在不同条件下反应可生成多种化工产品,如环酯J。其中G的分子式为C4H4O4。
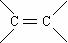 提示:有机物分子结构中的
比-OH更容易被氧化。
提示:有机物分子结构中的
比-OH更容易被氧化。
请按要求填空:
⑴写出下列反应的反应类型:⑥_________,⑧___________。
⑵写出结构简式:B_________________。
⑶写出下列反应的化学方程式:
③____________________________________________________________________;
⑩____________________________________________________________________。
⑷依据题意,写出④、⑤两步转化中所需无机物的化学式:④_______,⑤__________。
⑸写出符合下列条件的J的同分异构体:4个碳原子在同一直线上、二元酸酯。
_________________________________________________________。
6. 2008北京奥运会吉祥物福娃,已被做成各种玩具。有一种玩具的内充物为无
毒的聚酯纤维P,其合成线路如下,其中A、B、C、D、E均为有机物。
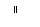
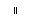
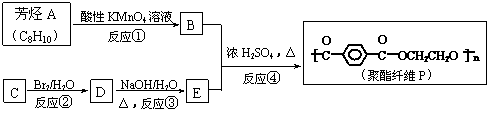 (1)A的结构简式是
,C的结构简式是
。
(1)A的结构简式是
,C的结构简式是
。
(2)反应②的化学方程式是 ;
 反应④的化学方程式是 。
反应④的化学方程式是 。
(3)等物质的量的B与E在热的浓硫酸存在的条件下反应,生成1mol有机物x及1mol水,则有机物x的结构简式是 。
(4)指出下列有机反应类型:
反应②属于 反应;反应③属于 反应;反应④属于 反应。
(5)B的同分异构体有多种,其中某种同分异构体y的分子内含有苯环,且y既能与NaHCO3溶液反应放出CO2气体,又能发生银镜反应,还能发生水解反应。则y的结构简式是 (只写一种)。
5. 已知:
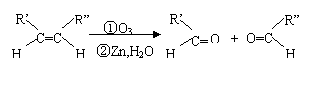
某一元氯代烃A分之式为C6H11Cl,可以发生如下图所示的转化:
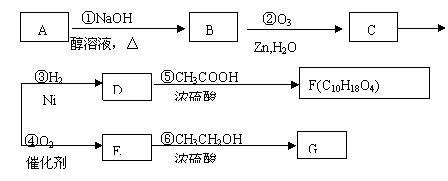
结构分析表明F分之中含有两个甲基,请回答下列问题:
(1)G的分子式为______________________
(2)写出A、E的结构简式:A________________,E_____________________。
 (3)D
F的反应方程式是___________________________
(3)D
F的反应方程式是___________________________
(4)分之式和E相同,主链含有3个碳原子的二元羧酸的同分异构有___________种。
4. 已知反应:
现有物质B-I的转化关系如下图:
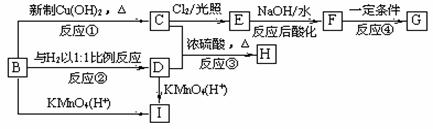
若B的分子式为C8H8O,其苯环上的一元取代物只有两种;G为高分子化合物。请回答下列问题:
(1)反应②的反应类型是 。
(2)写出有关物质的结构简式:F ,I 。
(3)写出下列反应的化学方程式:
B→C ;
 C+D→H
。
C+D→H
。
(4)C的同素分异构体且属于酯类的芳香族化合物共有6种,以下已有三种,请写出另三种同分异构体的结构简式:
 、
;
、
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com