
3、求曲线 在点M(2,6)处的切线方程.
在点M(2,6)处的切线方程.
(1)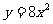 (2)
(2)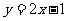 (3)
(3)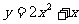 (4)
(4)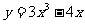
(5)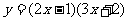 (6)
(6)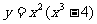
2、已知曲线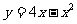 上有两点A(4,0),B(2,4),求:
上有两点A(4,0),B(2,4),求:
(1)割线AB的斜率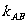 ;(2)过点A处的切线的斜率
;(2)过点A处的切线的斜率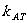 ;(3)点A处的切线的方程.
;(3)点A处的切线的方程.
2、导数的运算法则:
如果函数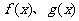 有导数,那么
有导数,那么
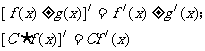
也就是说,两个函数的和或差的导数,等于这两个函数的导数的和或差;常数与函数的积的导数,等于常数乘函数的导数.
例1:求下列函数的导数:
(1)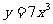 (2)
(2)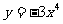 (3)
(3)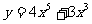
(4)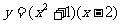 (5)
(5)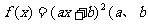 为常数)
为常数)
例2:已知曲线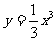 上一点
上一点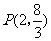 ,求:
,求:
(1)过点P的切线的斜率; (2)过点P的切线方程.
1、两个常用函数的导数:
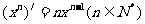
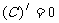
2、根据导数的定义求下列函数的导数:
(1)常数函数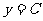 (2)函数
(2)函数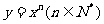





1、已知函数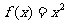 ,由定义求
,由定义求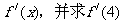



20.(2006湖北理)已知二次函数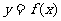 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为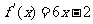 ,数列
,数列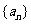 的前n项和为
的前n项和为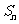 ,点
,点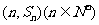 均在函数
均在函数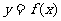 的图像上。 (Ⅰ)求数列
的图像上。 (Ⅰ)求数列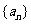 的通项公式;
的通项公式;
(Ⅱ)设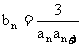 ,
,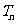 是数列
是数列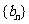 的前n项和,求使得
的前n项和,求使得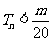 对所有
对所有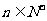 都成立的最小正整数m;
都成立的最小正整数m;
历届高考中的“等差数列”试题精选(自我测试)
19.(2006北京文)设等差数列{an}的首项a1及公差d都为整数,前n项和为Sn.
(Ⅰ)若a11=0,S14=98,求数列{an}的通项公式;
(Ⅱ)若a1≥6,a11>0,S14≤77,求所有可能的数列{an}的通项公式.
18.(据2005春招北京理改编)已知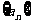 是等差数列,
是等差数列,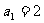 ,
,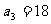 ;
;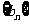 也是等差数列,
也是等差数列,
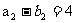 ,
,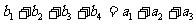 。
。
(1)求数列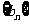 的通项公式及前
的通项公式及前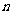 项和
项和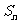 的公式;
的公式;
(2)数列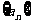 与
与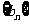 是否有相同的项? 若有,在100以内有几个相同项?若没有,请说明理由。
是否有相同的项? 若有,在100以内有几个相同项?若没有,请说明理由。
17.(2000全国、江西、天津文)设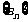 为等差数列,
为等差数列,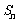 为数列
为数列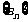 的前
的前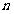 项和,已知
项和,已知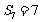 ,
,
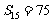 ,
,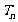 为数列
为数列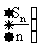 的前
的前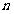 项和,求
项和,求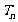 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com