
7.(2010·青岛模拟)已知函数f (x)=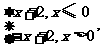 则不等式f (x)≥x 2的解集为 ( )
则不等式f (x)≥x 2的解集为 ( )
A.[-1,1] B.[-2,2] C.[-2,1] D.[-1,2]
解析:当x≤0时,不等式f
(x)≥x2化为x+2≥x2,即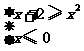 ,所以-1≤x≤0;
,所以-1≤x≤0;
当x>0时,不等式f
(x)≥x2化为-x+2≥x2,即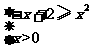 所以0<x≤1.
所以0<x≤1.
综上可得不等式的解集为[-1,1].
答案:A
6.已知函数f(x)的定义域为(0,+∞),且f (x)=2f (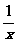 )
)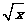 -1,则f(x)= .
-1,则f(x)= .
解析:考虑到所给式子中含有f
(x)和f (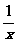 ),故可考虑利用换元法进行求解.
),故可考虑利用换元法进行求解.
在f (x)=2f
(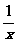 )-1,用
)-1,用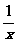 代替x,得f (
代替x,得f (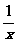 )=2f
(x)
)=2f
(x)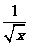 -1,将f (
-1,将f (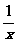 )=
)=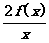 -1代入f (x)=2f
(
-1代入f (x)=2f
(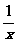 )-1中,可求得f (x)=+.
)-1中,可求得f (x)=+.
答案:+
|
题组三 |
分 段 函 数 |
5.已知f
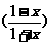 =
=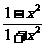 ,则f(x)的解析式为
( )
,则f(x)的解析式为
( )
A. f (x)=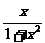 B.
f (x)=
B.
f (x)=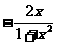

C.
f (x)=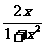 D. f (x)=
D. f (x)=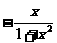
解析:由f
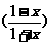 =
=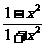 ,令t=
,令t=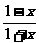 ,
,
则x=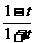 ,
,
∴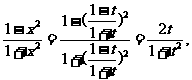
即f(t)=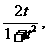
∴f(x)=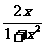 .
.
答案:C
4.已知函数f (x)的图象是两条线段(如图,不含端点),则f [f ()]= ( )
A.- B. C.- D.
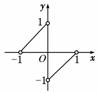 解析:由图象知f(x)=
解析:由图象知f(x)=
∴f ()=-1=-,
∴f [f ()]=f (-)=-+1=.
答案:B
3.已知两个函数f (x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表:
|
x |
1 |
2 |
3 |
|
f (x) |
2 |
3 |
1 |
|
x |
1 |
2 |
3 |
|
g( x ) |
3 |
2 |
1 |
则方程g [f (x)]=x的解集为 ( )
A.{1} B.{2} C.{3} D.∅
解析:当x=1时,g[f(1)]=g(2)=2,不合题意;
当x=2时,g[f(2)]=g(3)=1,不合题意;
当x=3时,g[f(3)]=g(1)=3,符合题意.
答案:C
|
题组二 |
函数的表示方法 |
2.下列各组函数中,表示同一函数的是 ( )
A.y=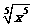 与y=
与y=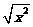
B.y=lnex与y=elnx
C.y=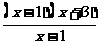 与y=x+3
与y=x+3
D.y=x0与y=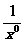
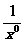 解析:对于命题A,对应关系不同;对于命题B,定义域不同;对于命题C,定义域不同;对于命题D,y=x0(x≠0)与y=
(x≠0)
解析:对于命题A,对应关系不同;对于命题B,定义域不同;对于命题C,定义域不同;对于命题D,y=x0(x≠0)与y=
(x≠0) 完全相同.
完全相同.
答案:D
1.设f:x→x2是从集合A到集合B的映射,如果B={1,2},则A∩B为 ( )
A.∅ B.{1} C.∅或{2} D.∅或{1}
解析:由已知x2=1或x2=2,解之得x=±1或x=±.若1∈A,则A∩B={1},若1∉A,则A∩B=∅.故A∩B=∅或{1}.
答案:D
(17)(本小题满分12分)
已知函数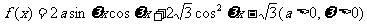 的最大值为
的最大值为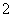 ,
,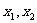 是集合
是集合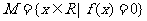 中的任意两个元素,且|
中的任意两个元素,且| |的最小值为
|的最小值为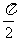 。
。
(I)求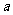 ,
,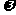 的值;
的值;
(II)若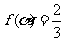 ,求
,求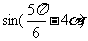 的值
的值
(18)(本小题满分12分)
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(I)求证:EF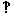 平面PAD;
平面PAD;
(II)求平面EFG与平面ABCD所成锐二面角的大小;
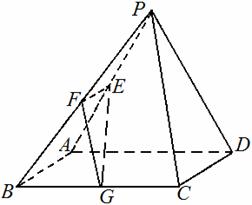 (III)若M为线段AB上靠近A的一个动点,问当AM长度等于多少时,直线MF与平面EFG所成角的正弦值等于
(III)若M为线段AB上靠近A的一个动点,问当AM长度等于多少时,直线MF与平面EFG所成角的正弦值等于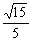 ?
?
(19)(本小题满分1 2分)
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖,盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽” 或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(I)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,从盒中抽取两张都是“世博会会徽“卡的概率是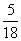 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(II)现有甲、乙、丙、丁四人依次抽奖,用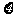 表示获奖的人数,求
表示获奖的人数,求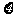 的分布列及
的分布列及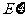 ,
,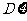 的值.
的值.
(20)(本小题满分12分)
点M在椭圆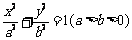 上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
(I)若圆M与y轴相交于A、B两点,且△ABM是边长为2的正三角形,求椭圆的方程;
(II)已知点F(1,0),设过点F的直线l交椭圆于C、D两点,若直线l绕点F任意转动时,恒有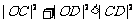 成立,求实数
成立,求实数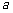 的取值范围.
的取值范围.
(21)(本小题 满分12分)
满分12分)
已知函数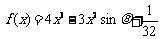 的极小值大于零,其中
的极小值大于零,其中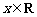 ,
,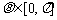 .
.
(I)求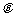 的取值范围;
的取值范围;
(II)若在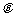 的取值范围内的任意
的取值范围内的任意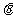 ,函数
,函数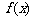 在区间
在区间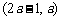 内都是增函数,求实数
内都是增函数,求实数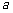 的取值范围;
的取值范围;
(III)设 ,
,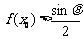 ,若
,若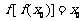 ,求证:
,求证: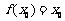 .
.
请考生在(22)、(23)、(24)三题中任选一题作答,如果多答,则按答题位置最前的题计分.作答时用2B铅笔在答题卡上把所选题目对应题号右侧的方框涂黑.
(22)(本小题满分10分)选修4-1:几何证明选讲
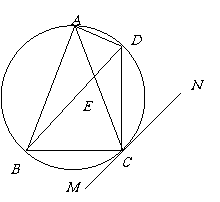
如图: 是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD//MN,AC与BD相交于点E。
 (I)求证:
(I)求证: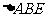

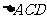 ;
;
(II)若AB=6,BC=4 ,求AE。
,求AE。
(23)(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线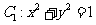 ,将
,将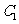 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的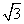 、2倍后得到曲线
、2倍后得到曲线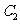 . 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
. 以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线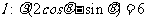 .
.
(I)试写出直线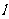 的直角坐标方程和曲线
的直角坐标方程和曲线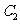 的参数方程;
的参数方程;
(II)在曲线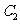 上求一点P,使点P到直线
上求一点P,使点P到直线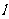 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
(24)(本小题满分10分)选修4-5:不等式选讲
(I)已知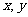 都是正实数,求证:
都是正实数,求证: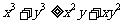 ;
;
(II)已知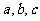 都是正实数,求证:
都是正实数,求证: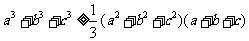 .
.
2011年辽宁省丹东市四校协作体第一次联合考试
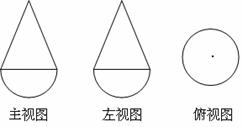
(13)已知一个几何体是由上下两部分构成的组合体,其三视图如下,若图中圆的半径为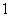 ,等腰三角形的腰长为
,等腰三角形的腰长为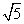 ,则该几何体的体积是
;
,则该几何体的体积是
;
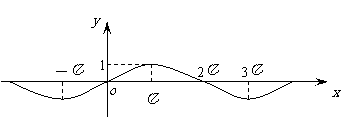
(14)已知函数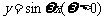 的图象如图所示,把
的图象如图所示,把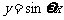 的图象所有点向右平移
的图象所有点向右平移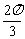 个单位后,再把所得函数图象上所有点得横坐标变为原来的
个单位后,再把所得函数图象上所有点得横坐标变为原来的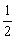 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数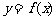 的图象,则
的图象,则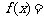 ;
;

(15)定义在R上的单调递减函数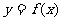 满足
满足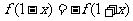 ,且对于任意
,且对于任意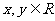 ,
, 不等式
不等式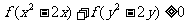 恒成立,则当
恒成立,则当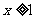 时,
时,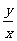 的取值范围为
;
的取值范围为
;
(16)某公司计划在北 京、丹东、沈阳、大连四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该公司不同的投资方案种数是
.(用数字作答)
京、丹东、沈阳、大连四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该公司不同的投资方案种数是
.(用数字作答)
(1)已知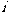 是虚数单位,复数
是虚数单位,复数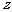 的共轭复数是
的共轭复数是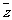 ,若
,若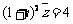 ,则
,则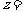
(A)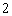 (B)
(B)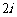 (C)
(C)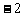 (D)
(D)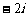
(2)在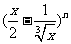 的展开式中,只有第5项的二项式系数最大,则展开式中常数项是
的展开式中,只有第5项的二项式系数最大,则展开式中常数项是
(A)7 (B)-28 (C)-7 (D)28
(3)甲、已乙两名篮球运动员每场比赛的得分情况用茎叶图表示如下:
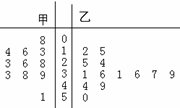 则下列说法中正确的个数为
则下列说法中正确的个数为
⑴甲得分的中位数为26,乙得分的中位数为36;
⑵甲、乙比较,甲的稳定性更好;
⑶乙有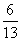 的叶集中在茎3上
的叶集中在茎3上
⑷甲有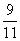 的叶集中在茎1、2、3上。
的叶集中在茎1、2、3上。
(A)1 (B)2 (C)3 (D)4
(4)若将函数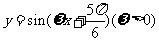 的图象向右平移
的图象向右平移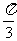 个单位长度后,与函数
个单位长度后,与函数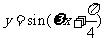 的图象重合,则
的图象重合,则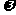 的最小值为
的最小值为
(A)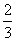 (B)
(B)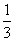 (C)
(C) 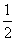 (D)
(D)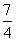
(5)已知数列{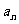 }满足
}满足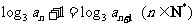 ,且
,且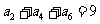 ,则
,则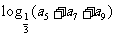 的值是
的值是
(A)5
(B)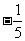 (C)-5
(D)
(C)-5
(D) 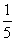
(6)已知命题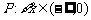 ,
,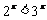 ;命题
;命题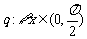 ,
,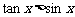 .则下列命题为真命题的是
.则下列命题为真命题的是
(A) (B)
(B)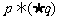 (C)
(C) (D)
(D)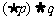
(7)已知平面向量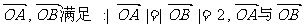 的夹角为
的夹角为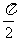 ,又
,又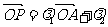
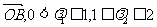 ,则点P的集合所表示的图形面积为
,则点P的集合所表示的图形面积为
(A)8 (B)4 (C)2 (D)1
(8)有编号为1,2,…,1000的产品,现需从中抽取所有编号能被3整除的产品作为样品进行检验,下面是四位同学设计的输出样品编号的程序框图:
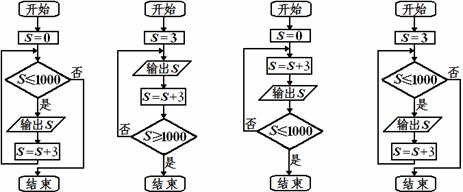
其中正确程序框图的个数是
(A)0 ( B)1 (C)2 (D)3
B)1 (C)2 (D)3
(9)已知P为双曲线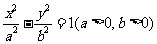 左支上一点,
左支上一点,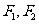 为双曲线的左右焦点,且
为双曲线的左右焦点,且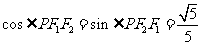 则此双曲线离心率是
则此双曲线离心率是
(A)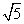 (B)5
(C)2
(B)5
(C)2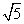 (D)3
(D)3
(10)某五所大学进行自主招生,同时向一所重点中学的五位学习成绩优秀,并在某些方面有特长的学生发出提前录取通知单.若这五名学生都乐意进这五所大学中的任意一所就读,则仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)的概率是
(A)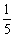 (B)
(B)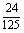 (C)
(C)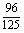 (D)
(D)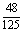
(11)已知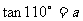 ,求
,求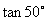 时,同学甲利用两角差的正切公式求得:
时,同学甲利用两角差的正切公式求得: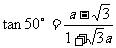 ;同学乙利用二倍角公式及诱导公式得
;同学乙利用二倍角公式及诱导公式得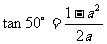 ;根据上述信息可估算
;根据上述信息可估算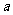 的范围是
的范围是
(A)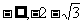 (B)
(B)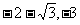
(C)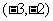 (D)
(D)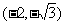
(12)在直角坐标系中横纵坐标为整数的点称为“格点”,如果函数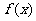 的图像恰好通过
的图像恰好通过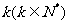 个格点,则称函数
个格点,则称函数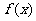 为k阶格点函数,下列函数中“一阶格点”函数有
为k阶格点函数,下列函数中“一阶格点”函数有
①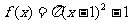 ②
②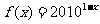
③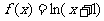 ④
④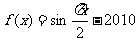
(A)②③ (B)①③ (C)①④ (D)②④
(C)①④ (D)②④
第II卷
本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题-第(24)题为选考题,考生根据要求做答.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com