
7. 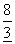 ;
8.
;
8. 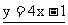 ; 9.
; 9. 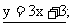 10.
10. 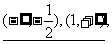 5 ,
5 , 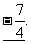
6.(提示: 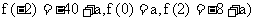
(二) 专题测试与练习
(一) 典型例题
例1. 解:(1) A
; (2) 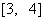 .
.
例2. 解:(1) 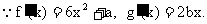
由题意得: 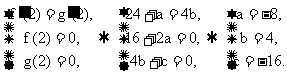
(2) 由(1)得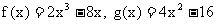
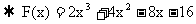
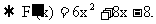 由
由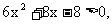 得:
得: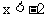 或
或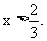
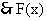 的递增区间是
的递增区间是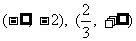 ;
; 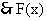 的递减区间是
的递减区间是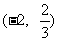 .
.
例3. 解:(1)
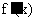
 , 若
, 若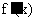
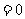 , 则
, 则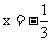 ,
, 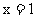
当x变化时,
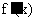 ,
,  变化情况如下表:
变化情况如下表:
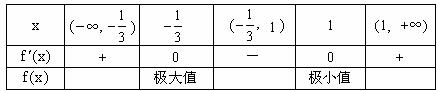
∴ 的极大值是
的极大值是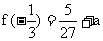 , 极小值是
, 极小值是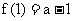 .
.
(2) 函数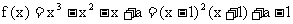 .
.
由此可知,
取足够大的正数时, 有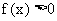 , 取足够小的负数时有
, 取足够小的负数时有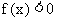 ,
,
所以曲线y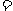
 与x轴至少有一个交点, 结合
与x轴至少有一个交点, 结合 的单调性可知:
的单调性可知:
当 的极大值
的极大值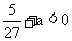 , 即
, 即 时, 它的极小值也小于0,
时, 它的极小值也小于0,
因此曲线y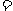
 与x轴仅有一个交点, 它在
与x轴仅有一个交点, 它在 上.
上.
当 的极小值
的极小值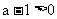 即
即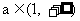 时, 它的极大值也大于0, 因此曲线
时, 它的极大值也大于0, 因此曲线
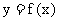 与x轴仅有一个交点, 它在
与x轴仅有一个交点, 它在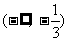 上.
上.
∴当
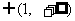 时, 曲线y
时, 曲线y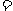
 与x轴仅有一个交点.
与x轴仅有一个交点.
11. 已知函数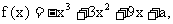
(1) 求 的单调递减区间;
的单调递减区间;
(2) 若 在区间
在区间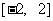 上的最大值为20, 求它在该区间上的最小值.
上的最大值为20, 求它在该区间上的最小值.
12. 已知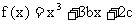 , 若函数
, 若函数 的一个极值点落在
的一个极值点落在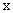 轴上, 求
轴上, 求 的值.
的值.
13. 已知函数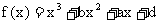 的图象过点P
的图象过点P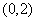 , 且在点M
, 且在点M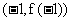 处的切线
处的切线
方程为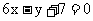 .
.
(1) 求函数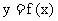 的解析式; (2) 求函数
的解析式; (2) 求函数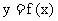 的单调区间.
的单调区间.
14. 已知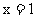 是函数
是函数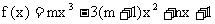 的一个极值点, 其中
的一个极值点, 其中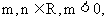
(1) 求m与n的关系式; (2) 求 的单调区间;
的单调区间;
(3) 当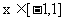 时, 函数
时, 函数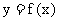 的图象上任意一点的切线斜率恒大于3m, 求m的取值
的图象上任意一点的切线斜率恒大于3m, 求m的取值
范围.
导数与函数(一)解答
10.函数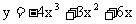 的单调递减区间为
, 极大值为
,极小值为
.
的单调递减区间为
, 极大值为
,极小值为
.
9. 曲线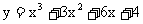 的所有切线中, 斜率最小的切线的方程是
.
的所有切线中, 斜率最小的切线的方程是
.
8. 曲线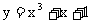 在点
在点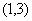 处的切线方程是
.
处的切线方程是
.
7. 曲线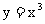 在点
在点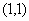 处的切线与x轴、直线
处的切线与x轴、直线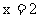 所围成的三角形的面积为 .
所围成的三角形的面积为 .
6. 已知:  为常数)在
为常数)在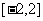 上有最大值是3, 那么
上有最大值是3, 那么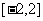 在上的最小
在上的最小
值是 ( )
A. 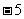 B.
B.
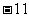 C.
C.
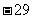 D.
D.
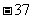
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com