
1.出现1道复合其它知识的圆锥曲线综合题;
2.与圆锥曲线有关的最值问题、参数范围问题,这类问题的综合型较大,解题中需要根据具体问题、灵活运用解析几何、平面几何、函数、不等式、三角知识,正确的构造不等式或方程,体现了解析几何与其他数学知识的联系。
预测2010年高考:
近年来圆锥曲线在高考中比较稳定,解答题往往以中档题或以押轴题形式出现,主要考察学生逻辑推理能力、运算能力,考察学生综合运用数学知识解决问题的能力。但圆锥曲线在新课标中化归到选学内容,要求有所降低,估计2007年高考对本讲的考察,仍将以以下三类题型为主.
1.求曲线(或轨迹)的方程,对于这类问题,高考常常不给出图形或不给出坐标系,以考察学生理解解析几何问题的基本思想方法和能力;
3.了解圆锥曲线的简单应用.
2.通过圆锥曲线与方程的学习,进一步体会数形结合的思想;
1.由方程研究曲线,特别是圆锥曲线的几何性质问题常化为等式解决,要加强等价转化思想的训练;
41.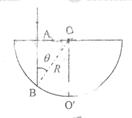 半圆柱体的横截面如图所示,
半圆柱体的横截面如图所示,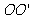 为半径。设从A点入射的光线在B点处恰好满足全反射条件,由折射定律有
为半径。设从A点入射的光线在B点处恰好满足全反射条件,由折射定律有
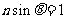
式中,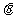 为全反射临界角。由几何关系得
为全反射临界角。由几何关系得
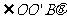 ②
②
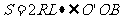 ③
③
代入题所给条件得
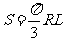 ④
④
40.解析:光线在AB面上折射时有sin60°=nsinα,在BC面上出射时,nsinβ=nsinγ
由几何关系,α+β=90°,δ=(60°-α)+(γ-β)=30°
 联立解得,α=β=45°,γ=60°,所以n=sin60°/sin45°=
联立解得,α=β=45°,γ=60°,所以n=sin60°/sin45°=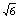 /2
/2
光在棱镜中的路程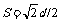 ,光在棱镜中光速
,光在棱镜中光速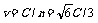
设垂直距离为L,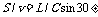 ,所以
,所以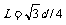
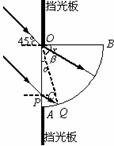
39.解:从O点射入的光线,折射角为r,根据折射定律,有: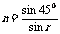 解得:r=30°
解得:r=30°
从某位置P点入射的光线,折射到AB弧面上Q点时,入射角恰等于临界角C,有:sinC=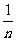
代入数据得: C=45°
ΔPQO中∠α=180°-90°-C-r=15°
所以能射出的光线区域对应的圆心角β=90°-α-r=45°
能射出光线的部分占AB面的比例为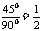
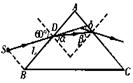
38.解:S发出的临界光线光路如图所示,由几何关系有
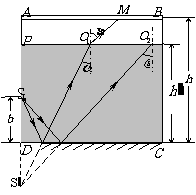
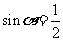 ①
①
根据折射定律有 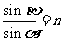 ②
②
由①②解得 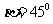
此横截面上标尺上被照亮的长度
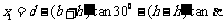 代入数据得
代入数据得 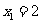 m
m
设此液体的临界角为θ,则
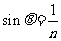
所示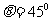
则液面上能射出光线部分的长度
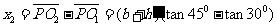
代入数据得 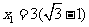 m=2.2m
m=2.2m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com