
9.二倍角公式:①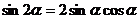 .
.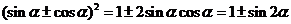
②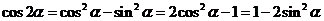 (升幂公式).
(升幂公式).
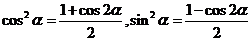 (降幂公式).
(降幂公式).
8.两角和与差的正弦、余弦、正切公式:
①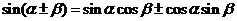 ;
;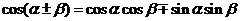 ;
;
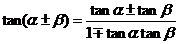 .
.
②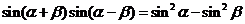 ;
;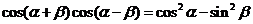 .
.
③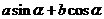 =
=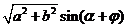 (其中,辅助角
(其中,辅助角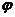 所在象限由点
所在象限由点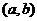 所在的象限
所在的象限
决定,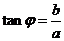 ).
).
7.三角函数的单调区间及对称性:
⑴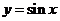 的单调递增区间为
的单调递增区间为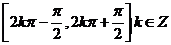 ,单调递减区间为
,单调递减区间为
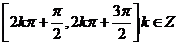 ,对称轴为
,对称轴为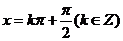 ,对称中心为
,对称中心为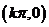
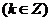 .
.
⑵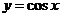 的单调递增区间为
的单调递增区间为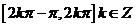 ,单调递减区间为
,单调递减区间为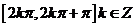 ,
,
对称轴为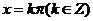 ,对称中心为
,对称中心为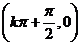
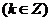 .
.
⑶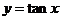 的单调递增区间为
的单调递增区间为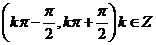 ,对称中心为
,对称中心为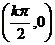
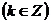 .
.
6.同角三角函数的基本关系: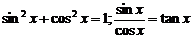
5.⑴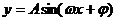 对称轴:令
对称轴:令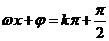 ,得
,得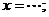 对称中心:
对称中心: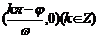 ;
;
⑵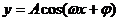 对称轴:令
对称轴:令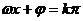 ,得
,得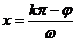 ;对称中心:
;对称中心: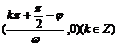 ;
;
⑶周期公式:①函数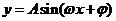 及
及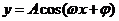 的周期
的周期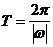 (A、ω、
(A、ω、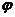 为常数,
为常数,
且A≠0).②函数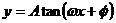 的周期
的周期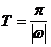 (A、ω、
(A、ω、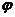 为常数,且A≠0).
为常数,且A≠0).
4.诱导公式记忆规律:“奇变偶不变,符号看象限”
3.三角函数符号规律:一全正,二正弦,三正切,四余弦;(简记为“全s t c”)
2.三角函数定义:角 终边上任一点(非原点)P
终边上任一点(非原点)P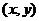 ,设
,设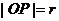 则:
则: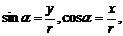
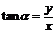
1.⑴角度制与弧度制的互化: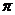 弧度
弧度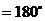 ,
,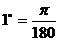 弧度,
弧度,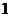 弧度
弧度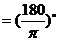
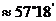
⑵弧长公式: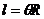 ;扇形面积公式:
;扇形面积公式: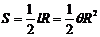 。
。
13.导数:
⑴导数定义:f(x)在点x0处的导数记作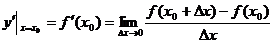
⑵常见函数的导数公式: ①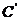
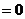 ;②
;②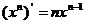 ;③
;③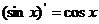 ;④
;④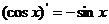 ;⑤
;⑤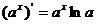 ;⑥
;⑥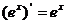 ;⑦
;⑦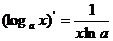 ;⑧
;⑧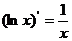 。
。
⑶导数的四则运算法则: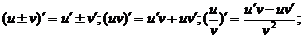
⑷(理科)复合函数的导数: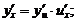
⑸导数的应用:
①利用导数求切线:注意:ⅰ)所给点是切点吗?ⅱ)所求的是“在”还是“过”该点的切线?
②利用导数判断函数单调性:i)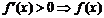 是增函数;ii)
是增函数;ii)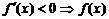 为减函数;iii)
为减函数;iii)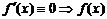 为常数;
为常数;
③利用导数求极值:ⅰ)求导数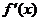 ;ⅱ)求方程
;ⅱ)求方程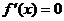 的根;ⅲ)列表得极值。
的根;ⅲ)列表得极值。
④利用导数求最大值与最小值:ⅰ)求极值;ⅱ)求区间端点值(如果有);ⅲ)比较得最值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com