
6、在正方体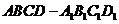 中,
中,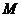 为
为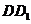 的中点,
的中点, 为底面
为底面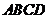 的中心,
的中心,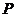 为棱
为棱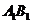 上任意一点,则直线
上任意一点,则直线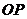 与直线
与直线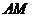 所成的角是(D )A.
所成的角是(D )A.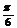 B.
B.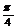 C.
C.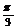 D.
D.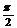
4、在棱长都相等的四面体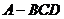 中,
中, 、
、 分别为棱
分别为棱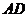 、
、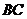 的中点,连接
的中点,连接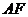 、
、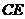 ,则直线
,则直线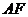 、
、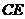 所成角的余弦值为: C A、 B、 C、 D、
所成角的余弦值为: C A、 B、 C、 D、
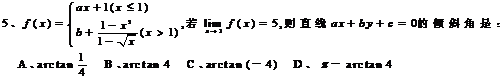 A
A
3、6名运动员站在6条跑道上准备参加比赛,其中甲不能站在第一道也不能站在第二道,乙必须站在第五道或第六道,则不同排法种数共有: AA、144 B、96 C、72 D、48
2、有一个容量为45的样本数据,分组后各组的频数如下:
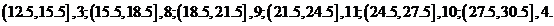 根据累积频率分布,估计不大于27.5的数据约为总体的 AA.91% B.92% C.95% D.30%
根据累积频率分布,估计不大于27.5的数据约为总体的 AA.91% B.92% C.95% D.30%
1、一个动点在三棱锥体内等可能出现,则该动点与下底面构成的三棱锥的体积超过原三棱锥体积的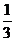 而不足原三棱锥体积的
而不足原三棱锥体积的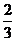 的概率为D A、
的概率为D A、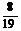 ; B、
; B、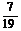 ; C、
; C、 ; D、
; D、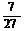 ;
;
21. (I)证:  三棱柱
三棱柱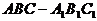 中
中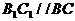 ,
,
又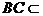 平面
平面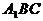 ,且
,且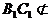 平面
平面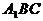 ,
, 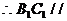 平面
平面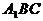
(II)证:
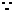 三棱柱
三棱柱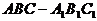 中
中 ,
, 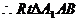 中
中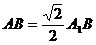
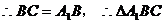 是等腰三角形 ,
是等腰三角形 ,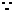 E是等腰
E是等腰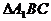 底边
底边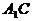 的中点,
的中点,
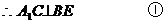 又依条件知
又依条件知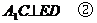 且
且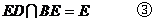
由①,②,③得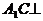 平面EDB
平面EDB
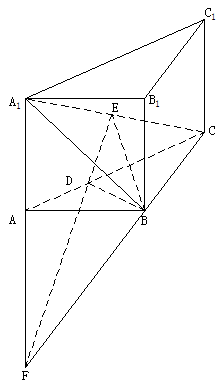
(III)解:
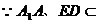 平面
平面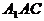 , 且
, 且 不平行,故延长
不平行,故延长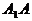 ,ED后必相交, 设交点为E,连接EF,如下图
,ED后必相交, 设交点为E,连接EF,如下图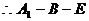 是所求的二面角
是所求的二面角
依条件易证明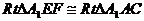
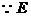 为
为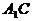 中点,
中点, 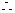 A为
A为 中点
中点
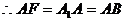
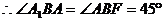
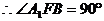
即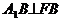 又
又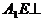 平面EFB,
平面EFB, 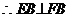
 是所求的二面角的平面角 ,
是所求的二面角的平面角 , 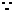 E为等腰直角三角形
E为等腰直角三角形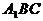 底边中点,
底边中点, 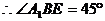
故所求的二面角的大小为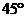
22 证明
证明 (1)当n=1时,42×1+1+31+2=91能被13整除
(1)当n=1时,42×1+1+31+2=91能被13整除
(2)假设当n=k时,42k+1+3k+2能被13整除,则当n=k+1时,
42(k+1)+1+3k+3=42k+1·42+3k+2·3-42k+1·3+42k+1·3
=42k+1·13+3·(42k+1+3k+2?)
∵42k+1·13能被13整除,42k+1+3k+2能被13整除
∴当n=k+1时也成立
由①②知,当n∈N*时,42n+1+3n+2能被13整除
20. 解:(I)设“甲队以3:0获胜”为事件A,则
(II)设“甲队获得总冠军”为事件B,
则事件B包括以下结果:3:0;3:1;3:2三种情况
若以3:0胜,则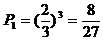 ;
;
若以3:1胜,则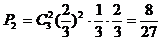
若以3:2胜,则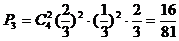
所以,甲队获得总冠军的概率为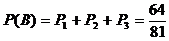
19. 解:(Ⅰ)证明:CD//C1B1,又BD=BC=B1C1,∴ 四边形BDB1C1是平行四边形,
∴BC1//DB1.又DB1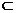 平面AB1D,BC1
平面AB1D,BC1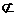 平面AB1D,∴直线BC1//平面AB1D.
平面AB1D,∴直线BC1//平面AB1D.
(Ⅱ)解:过B作BE⊥AD于E,连结EB1,∵B1B⊥平面ABD,∴B1E⊥AD ,
∴∠B1EB是二面角B1-AD-B的平面角,∵BD=BC=AB,∴E是AD的中点, 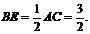 在Rt△B1BE中,
在Rt△B1BE中,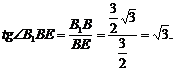 ∴∠B1EB=60°。即二面角B1-AD-B的大小为60°
∴∠B1EB=60°。即二面角B1-AD-B的大小为60°
21、直三棱柱ABC-A1B1C1中,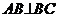 ,E是A1C的中点,
,E是A1C的中点,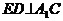 且交AC于D,
且交AC于D,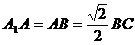 。(I)证明:
。(I)证明: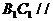 平面
平面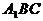 ;(II)证明:
;(II)证明: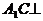 平面
平面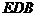 ;
;
(III)求平面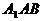 与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。
与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。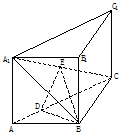
22 用数学归纳法证明4
用数学归纳法证明4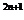 +3n+2能被13整除,其中n∈N*
+3n+2能被13整除,其中n∈N*
20、某篮球职业联赛总决赛在甲、乙两支球队之间进行,比赛采用五局三胜制,即哪个队先胜三场即可获得总冠军。已知在每一场比赛中,甲队获胜的概率均为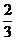 ,乙队获胜的概率均为
,乙队获胜的概率均为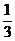 。求:(I)甲队以3:0获胜的概率;(II)甲队获得总冠军的概率。
。求:(I)甲队以3:0获胜的概率;(II)甲队获得总冠军的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com