
40.复数的相等: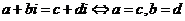 .(
.(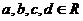 )
)
39.复合函数的求导法则: 设函数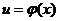 在点
在点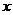 处有导数
处有导数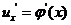 ,函数
,函数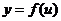 在点
在点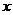 处的对应点U处有导数
处的对应点U处有导数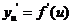 ,则复合函数
,则复合函数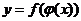 在点
在点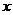 处有导数,且
处有导数,且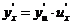 ,或写作
,或写作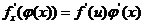 .
.
38.可导函数四则运算的求导法则:
①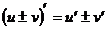 ;②
;②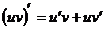 ,
,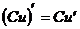 ;③
;③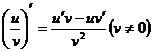 .
.
37.常见函数的导数:①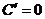 (
(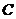 为常数);②
为常数);②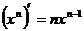
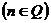 ;③
;③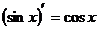 ;
;
④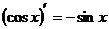 ;⑤
;⑤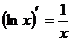 ,
,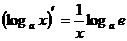 ;⑥
;⑥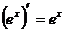 ,
,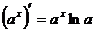 .
.
36.导数与函数的单调性的关系:
(1)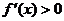 与
与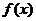 为增函数的关系:
为增函数的关系: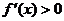 能推出
能推出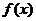 为增函数,但反之不一定.如函数
为增函数,但反之不一定.如函数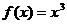 在
在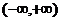 单调递增,但
单调递增,但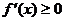 ,故
,故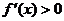 是
是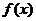 为增函数的充分不必要条件.
为增函数的充分不必要条件.
(2)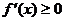 与
与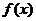 为增函数的关系:
为增函数的关系: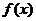 为增函数,一定可以推出
为增函数,一定可以推出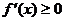 ,但反之不一定,因为
,但反之不一定,因为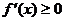 ,即为
,即为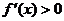 或
或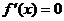 .当函数在某个区间内恒有
.当函数在某个区间内恒有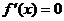 ,则
,则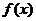 为常数,函数不具有单调性.∴
为常数,函数不具有单调性.∴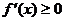 是
是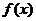 为增函数的必要不充分条件.
为增函数的必要不充分条件.
35.函数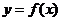 在点
在点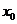 处的导数的几何意义:函数
处的导数的几何意义:函数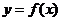 在点
在点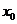 处的导数是曲线
处的导数是曲线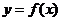
在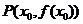 处的切线的斜率
处的切线的斜率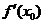 ,相应的切线方程是
,相应的切线方程是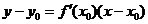
34.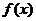 在
在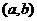 的导数
的导数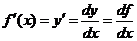
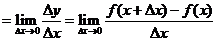 .
.
33.瞬时加速度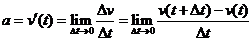 .
.
32.瞬时速度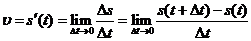 .
.
31.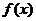 在
在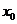 处的导数(或变化率或微商)
处的导数(或变化率或微商)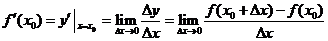 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com