
296.
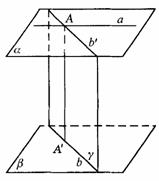
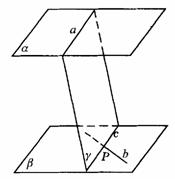
如图9-35,平面a
∥平面b ,△ABC、△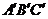 的分别在a 、b 内,线段
的分别在a 、b 内,线段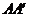 、
、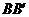 、
、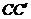 相交于点O,O在a 、b 之间.若AB=2,AC=1,∠ABC=60°,OA∶
相交于点O,O在a 、b 之间.若AB=2,AC=1,∠ABC=60°,OA∶ =3∶2,则△
=3∶2,则△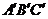 的面积为________.
的面积为________.
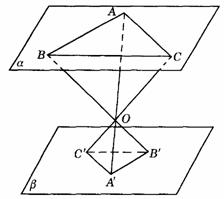
解析:图9-35
∵  ,∴
,∴ 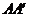 、
、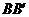 确定平面
确定平面 ,平面
,平面 ∩a =AB,平面
∩a =AB,平面 ,∵ a ∥b ,∴
,∵ a ∥b ,∴ 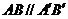 ,同理
,同理 ,
,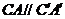 .由于方向相反,∴ △ABC与△
.由于方向相反,∴ △ABC与△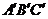 的三内角相等,∴ △ABC∽△
的三内角相等,∴ △ABC∽△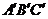 .且
.且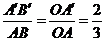 . ∵
. ∵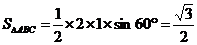 ,∴
,∴ 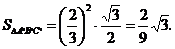
295. 已知空间不共面的四个点,与此四个点距离都相等的平面有________个.
解析:与不共面的四个点距离相等的平面分为两类,一类是四个点中一个点位于平面的一侧,另外三个点在平面的另一侧,这样的平面有4个;另一类是四个点中的两个点位于平面一侧,另外两个点在平面的另一侧,这样的平面有3个,故一共7个平面到这四个点距离相等.
294. 已知AC,BD是夹在两平行平面a 、b 间的线段,A∈a ,B∈a ,C∈b ,D∈b ,且AC=25cm,BD=30cm,AC、BD在平面b 内的射影的和为25cm,则AC、BD在平面b 内的射影长分别为________,AC与平面b 所成的角的正切值为________,BD与平面b 所成的角的正切值为________.
解析:设a 、b 间的距离为h,AC在平面b
内的射影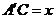 ,BD在平面b
内的射影
,BD在平面b
内的射影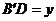 ,根据已知条件可得
,根据已知条件可得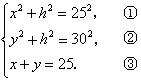 ②-①得
②-①得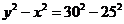 ,即
,即
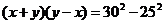 ,把③代入得y-x=11,∴
,把③代入得y-x=11,∴  解得
解得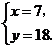 即
即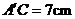 ,
,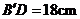 .又h=24cm,AC与平面b
所成的角为
.又h=24cm,AC与平面b
所成的角为 ,
,
 ,同理
,同理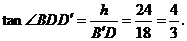
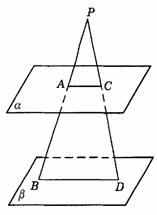
293. 平面a ∥平面b ,过平面a 、b 外一点P引直线PAB分别交a 、b 于A、B两点,PA=6,AB=2,引直线PCD分别交a 、b 于C、D两点.已知BD=12,则AC的长等于( ).
A.10 B.9 C.8 D.7
解析:B.如图答9-32,平面PBD∩a
=AC,平面PBD∩b =BD,∵ a
∥b ,∴ AC∥BD.由平面几何知识知,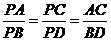 .∵ PA=6,AB=2,BD=12,∴
.∵ PA=6,AB=2,BD=12,∴ 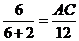 ,∴ AC=9.
,∴ AC=9.
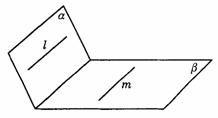
292. 设a 、b 是两个平面,l和m是两条直线,那么a ∥b 的一个充分条件是( ).
A.l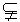 a ,m
a ,m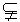 a ,且l∥b
,m∥b
B.l
a ,且l∥b
,m∥b
B.l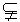 a ,m
a ,m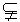 b ,且l∥m
b ,且l∥m
C.l⊥a ,m⊥b ,且l∥m D.l∥a ,m∥b ,且l∥m
解析:C.可参看图答9-31.
图答9-31
291. 给出下列命题,错误的命题是( ).
A.若直线a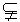 平面a ,且a ∥平面b ,则直线a与平面b 的距离等于平面a 、b 间的距离
平面a ,且a ∥平面b ,则直线a与平面b 的距离等于平面a 、b 间的距离
B.若平面a ∥平面b ,点A∈a ,则点A到平面b 的距离等于平面a 、b 间的距离
C.两条平行直线分别在两个平行平面内,则这两条直线间的距离等于这两个平行平面间的距离
D.两条异面直线分别在两个平行平面内,则这两条直线间的距离等于这两个平行平面间的距离
解析:C.以下按顺序说明,对A中,在a上任取一点P,作PH⊥b ,PH为直线a与平面b 的距离.∵ a ∥b ,PH⊥a ,∴ PH又为a 、b 间的距离.对于B,作AH⊥b ,AH的长为点A到b 的距离.又∵ a ∥b ,∴ AH⊥a ,于是AH的长是a 、b 两个平行平面间的距离.
对于C,设a∥b,a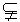 a ,b
a ,b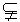 b ,过a上任一点P作PQ⊥b于Q,则PQ的长为a、b两平行直线间的距离.因为PQ与a 、b 不一定垂直,所以PQ的长一般不是a 、b
间的距离,一般地说,a、b间的距离不小于a 、b
间的距离.
b ,过a上任一点P作PQ⊥b于Q,则PQ的长为a、b两平行直线间的距离.因为PQ与a 、b 不一定垂直,所以PQ的长一般不是a 、b
间的距离,一般地说,a、b间的距离不小于a 、b
间的距离.
对于D.设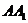 是异面直线a、b的公垂线段,A∈a,
是异面直线a、b的公垂线段,A∈a, ,a
,a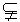 a ,b
a ,b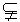 b ,过A和b的平面与a 相交于
b ,过A和b的平面与a 相交于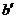 ,则
,则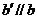 ,于是
,于是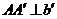 .∴
.∴  .同理
.同理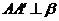 .故
.故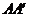 的长又是a 、b 两个平面间的距离(如图答9-30).
的长又是a 、b 两个平面间的距离(如图答9-30).
290. 给出以下命题:
①平行于同一条直线的两条直线平行;
②垂直于同一条直线的两条直线平行;
③平行于同一个平面的两条直线平行;
④垂直于同一个平面的两条直线平行;
⑤平行于同一条直线的两个平面平行;
⑥垂直于同一条直线的两个平面平行;
⑦平行于同一个平面的两个平面平行.
其中正确的命题是________(把你认为正确的命题的序号都写上).
解析:①、④、⑥、⑦.由公理4知①正确.由直线与平面垂直的性质定理知④正确.由两个平面平行判定定理可以推导出⑥、⑦正确.垂直于同一条直线的两条直线的位置关系是平行、相交、或异面;平行于同一个平面的两条直线的位置关系是平行、相交、或异面;平行于同一条直线的两个平面的位置关系是平行或相交.
289. .B.A不正确是因为直线b可以在平面a 内,也可能与a 平行,还可能与a 相交但不成直角,C中的直线b只与b 内的直线a垂直,不能得出垂直b 的结论.D中a 、b 可能相交,a 内的两条直线均与交线平行
288. 已知直线a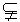 平面a ,直线b
平面a ,直线b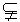 平面b ,a
平面b ,a 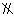 b,a∥b ,b∥a .求证:a ∥b .
b,a∥b ,b∥a .求证:a ∥b .
解析:如图答9-29,在b上任取一点P,由点P和直线a确定的平面g 与平面b 交于直线c,则c与b相交于点P.
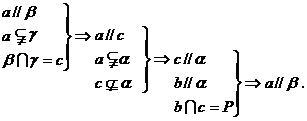
图答9-29
287. .三个不同平面a ,b ,g 满足a ∥b ,b ∩g =l,则a 与g 的位置关系是________;若三个平面满足a ∥b ,b ∥g ,则a 与g 的位置关系是________.
解析:相交;平行.作直线l⊥b
,∵ a ∥b ,∴ l⊥a ,∵ b
∥g ,∴ l⊥g
.∴ a ∥g .当a
∥b ,b ∩g
=l,假设a
与g 不相交,则a ∥g
,∵ a ∥b ,由前面证明可知b
∥g ,这与b 、g
相交矛盾.∴ a 与g 相交.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com