
§2. 物体的运动
22.(12分)已知函数f ( x )=x 2+ax+b
(1)若对任意的实数x都有f (1+x)=f (1-x) 成立,求实数 a的值;
(2)若f (x)满足f(-x)=f(x),求实数a的值;
(3)若f (x)在[ 1,+∞)内递增,求实数a的范围。
(选做).(14分)已知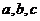 都是实数且
都是实数且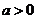 ,
,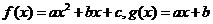 ,当
,当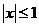 时,
时,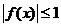 且
且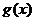 的最小值为-2。 1)证明:
的最小值为-2。 1)证明: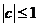 ;
2)求
;
2)求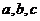 的值。
的值。
21. (本小题满分12分)
(本小题满分12分)
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.,
当每辆车的月租金定为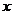 元时,租赁公司的月收益为
元时,租赁公司的月收益为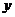 元,
元,
(1)试写出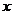 ,
,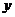 的函数关系式(不要求写出定义域);
的函数关系式(不要求写出定义域);
(2)租赁公司某月租出了88辆车,求租赁公司的月收益多少元?
19.(8分) 已知函数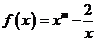 且
且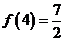 ,
,
(1)求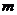 的值;
的值;
(2)判定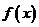 的奇偶性;
的奇偶性;
20 .(12分)已知函数
.(12分)已知函数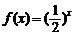 (x>0),g (x)是定义在R上的函数,且满足
(x>0),g (x)是定义在R上的函数,且满足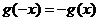 ;当x>0时,g (x)=f (x).求g (x)的表达式并画出图象.
;当x>0时,g (x)=f (x).求g (x)的表达式并画出图象.
18. (12分)化简: (1)(0.064) + 16 -- 0.75
- ()0 (2)lg2lg50 + lg25 - lg5lg20
(12分)化简: (1)(0.064) + 16 -- 0.75
- ()0 (2)lg2lg50 + lg25 - lg5lg20
17.(10分) 已知M={x| -2≤x≤5}, N={x| a+1≤x≤2a-1}.
(Ⅰ)若M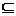 N,求实数a的取值范围;
N,求实数a的取值范围;
(Ⅱ)若M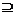 N,求实数a的取值范围.
N,求实数a的取值范围.
16.函数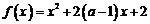 在区间
在区间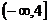 上是减函数,则实数
上是减函数,则实数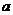 的取值范围是________________________
的取值范围是________________________
15.函数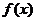 是定义在R上的奇函数,并且当
是定义在R上的奇函数,并且当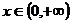 时,
时,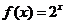 ,那么,
,那么,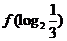 =
.
=
.
13.设集合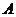 ={1,2},
={1,2}, 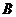 ={2,3},
={2,3}, 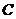 ={2,3,4},则(
={2,3,4},则(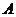 ∩
∩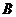 )∪
)∪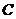 = .
= .
14.函数y = log0.5(2 - x2)的值域是_____________________________
12.函数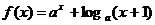 (
(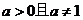 )在
)在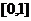 上的最大值与最小值之和为
上的最大值与最小值之和为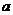 ,则
,则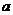 的值为(
).
的值为(
).
A.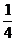 B.
B.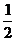 C.2 D.4
C.2 D.4
第Ⅱ卷 (非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com