
12. 设F1、F2分别为椭圆C: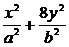 =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,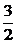 )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线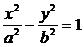 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
第二讲 双曲线
[知识梳理]
[知识盘点]
11. 椭圆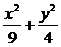 =1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,求点P横坐标的取值范围。
=1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,求点P横坐标的取值范围。
10.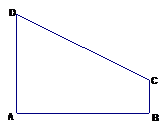 (2007年广东韶关调研)如图,在直角梯形
(2007年广东韶关调研)如图,在直角梯形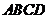 中,
中,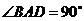 ,
,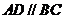 ,
,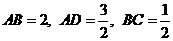 ,椭圆以
,椭圆以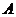 、
、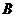 为焦点且经过点
为焦点且经过点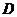 .建立适当的直角坐标系,求椭圆的方程;
.建立适当的直角坐标系,求椭圆的方程;
9.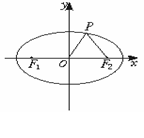 如图所示,F1、F2分别为椭圆
如图所示,F1、F2分别为椭圆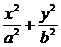 =1的左、右焦点,点P在椭圆上,△POF2是面积为
=1的左、右焦点,点P在椭圆上,△POF2是面积为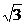 的正三角形,则b2的值是__
___.
的正三角形,则b2的值是__
___.
8.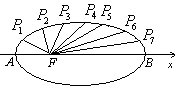 (2006年四川卷)如图,把椭圆
(2006年四川卷)如图,把椭圆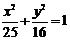 的长轴
的长轴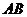 分成
分成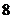 等份,过每个分点作
等份,过每个分点作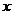 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于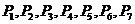 七个点,
七个点,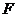 是椭圆的一个焦点,则
是椭圆的一个焦点,则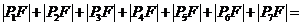 _______________
_______________
7.(2007年广东惠州市调研)已知点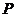 是椭圆
是椭圆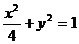 上的在第一象限内的点,又
上的在第一象限内的点,又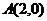 、
、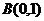 ,
,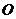 是原点,则四边形
是原点,则四边形 的面积的最大值是_________
的面积的最大值是_________
6.已知椭圆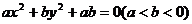 ,则其焦点坐标为____________.
,则其焦点坐标为____________.
5.(2006年湖北卷)设过点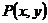 的直线分别与
的直线分别与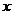 轴的正半轴和
轴的正半轴和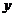 轴的正半轴交于
轴的正半轴交于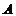 、
、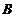 两点,点
两点,点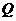 与点
与点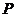 关于
关于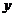 轴对称,
轴对称,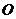 为坐标原点,若
为坐标原点,若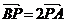 ,且
,且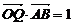 ,则
,则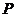 点的轨迹方程是( )
点的轨迹方程是( )
(A) 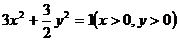 (B)
(B)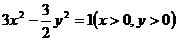
(C)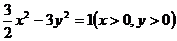 (D)
(D) 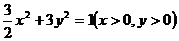
4.如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是( )
(A)(0,+∞) (B)(0,2) (C)(1,+∞) (D)(0,1)
3.椭圆短轴长是2,长轴是短轴的2倍,则椭圆中心到其准线距离是( )
(A)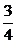 (B)
(B)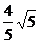 (C)
(C)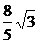 (D)
(D)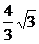
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com