
18.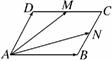 (本小题满分12分)如图,在平行四边形ABCD中,
(本小题满分12分)如图,在平行四边形ABCD中,
M,N分别为DC,BC的中点,已知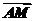 =c,
=c,
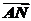 =d,试用c,d表示
=d,试用c,d表示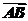 ,
,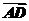 .
.
解:法一:设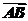 =a,
=a,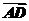 =b,则
=b,则
a=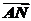 +
+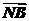 =d+(-b),
①
=d+(-b),
①
b=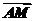 +
+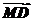 =c+(-a), ②
=c+(-a), ②
将②代入①得a=d+(-)[c+(-a)]
⇒a=d-c,代入②
得b=c+(-)(d-c)=c-d.
故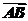 =d-c,
=d-c,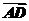 =c-d.
=c-d.
法二:设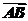 =a,
=a,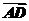 =b.
=b.
所以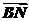 =b,
=b,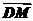 =a,
=a,
因而⇒,
即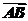 =(2d-c),
=(2d-c),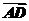 =(2c-d).
=(2c-d).
17.(本小题满分12分)已知复数z满足:|z|=1+3i-z,化简
解:设z=a+bi(a,b∈R),而|z|=1+3i-z,即-1-3i+a+bi=0,
则,⇒
∴z=-4+3i.
∴===3+4i.
16.在直角坐标系xOy中,i、j分别是与x轴,y轴平行的单位向量,若直角三角形ABC中,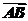 =i+j,
=i+j,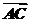 =2i+mj,则实数m=________.
=2i+mj,则实数m=________.
解析:本题考查了向量的运算.由已知可得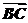 =
=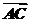 -
-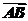 =i+(m-1)j.
=i+(m-1)j.
当A=90°时,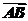 ·
·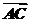 =(i+j)·(2i+mj)=2+m=0,m=-2.
=(i+j)·(2i+mj)=2+m=0,m=-2.
当B=90°时,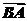 ·
·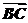 =-(i+j)·[i+(m-1)·j]=-(1+m-1)=-m=0,m=0.
=-(i+j)·[i+(m-1)·j]=-(1+m-1)=-m=0,m=0.
当C=90°时,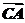 ·
·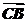 =-(2i+mj)·[-i-(m-1)j]=2+m(m-1)=m2-m+2=0,此时m不存在.故m=0或-2.
=-(2i+mj)·[-i-(m-1)j]=2+m(m-1)=m2-m+2=0,此时m不存在.故m=0或-2.
答案:0或-2
15.已知平面向量a,b,c满足a+b+c=0,且a与b的夹角为135°,c与b的夹角为120°,|c|=2,则|a|=________.
解析:根据已知条件,组成以|a|,|b|,|c|为边长的三角形,由正弦定理得=,又|c|=2,所以|a|=.
答案:
14.(文)若向量a=(1+2λ,2-3λ)与b=(4,1)共线,则λ=________.
解析:依题意得4(2-3λ)-(1+2λ)=0,由此解得λ=.
答案:
(理)已知a=(3,2),b(-1,2),(a+λb)⊥b,则实数λ=________.
解析:∵(a+λb)⊥b,
∴(a+λb)·b=a·b+λb2=1+5λ=0,∴λ=-.
答案:-
13.已知复数z1=m+2i,z2=3-4i,若为实数,则实数m=________.
解析:===是实数,∴6+4m=0,故m=-.
答案:-
12.设a=(a1,a2),b=(b1,b2).定义一种向量积:
a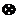 b=(a1,a2)
b=(a1,a2) 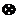 (b1,b2)=(a1b1,a2b2).已知m=,n=,点P(x,y)在y=sinx的图象上运动 ,点Q在y=f(x)的图象上运动,满足
(b1,b2)=(a1b1,a2b2).已知m=,n=,点P(x,y)在y=sinx的图象上运动 ,点Q在y=f(x)的图象上运动,满足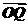 =m
=m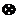
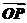 +n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别为
( )
+n(其中O为坐标原点),则y=f(x)的最大值A及最小正周期T分别为
( )
A.2,π B.2,4π C.,4π D.,π
解析:设Q(x0,y0),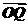 =(x0,y0),
=(x0,y0),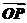 =(x,y),
=(x,y),
∵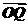 =m
=m
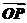 +n,
+n,
∴(x0,y0)=?(x,y)+=+=,
∴⇒
代入y=sinx中得,2y0=sin,
所以最大值为,周期为4π.
答案:C
11.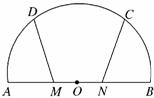 如图,AB是半圆O的直径,C,D是弧AB的三等分点,
如图,AB是半圆O的直径,C,D是弧AB的三等分点,
M,N是线段AB的三等分点,若OA=6,
则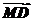 ·
·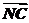 的值为
( )
的值为
( )
A.13 B.26 C.18 D.36
解析: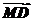 ·
·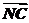 =(
=(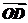 -
-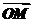 )·(
)·(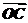 -
-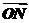 )=
)=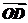 ·
·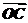 -
-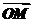 ·
·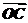 -
-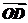 ·
·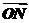 +
+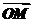 ·
·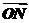 =6×6cos60°-6×2cos120°-6×2cos120°+2×2cos180°=26.
=6×6cos60°-6×2cos120°-6×2cos120°+2×2cos180°=26.
答案:B
10.已知非零向量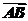 ,
,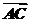 和
和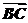 满足
满足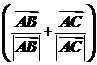 ·
·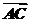 =0,且
=0,且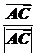 ·
·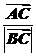 =,则△ABC为
( )
=,则△ABC为
( )
A.等边三角形 B.等腰非直角三角形
C.非等腰三角形 D.等腰直角三角形
解析: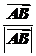 、
、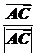 、
、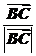 均为单位向量.
均为单位向量.
由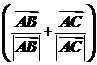 ·
·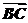 =0,得|
=0,得|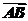 |=|
|=|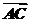 |.
|.
由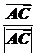 ·
·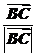 =1×1×cosC=,得C=45°.
=1×1×cosC=,得C=45°.
故三角形为等腰直角三角形.
答案:D
9.(2010·黄冈模拟)已知A、B、C是锐角△ABC的三个内角,向量p=(1+sinA,1+cosA),q=(1+sinB,-1-cosB),则p与q的夹角是 ( )
A.锐角 B.钝角 C.直角 D.不确定
解析:锐角△ABC中,sinA>cosB>0,sinB>cosA>0,
故有p·q=(1+sinA)(1+sinB)-(1+cosA)(1+cosB)>0,同时易知p与q方向不相同,故p与q的夹角是锐角.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com