
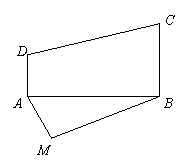
6.如图所示,某农场在M处有一堆肥料沿道路MA或MB送到大田ABCD中去,已知|MA|=6,|MB|=8,|BC|=3,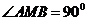 ,能否在大田中确定一条界线,使位于界线一侧的点沿MA送肥料较近,而另一侧沿MB送肥料较近?若能,请建立适当的直角坐标系,求出这条界线的方程.
,能否在大田中确定一条界线,使位于界线一侧的点沿MA送肥料较近,而另一侧沿MB送肥料较近?若能,请建立适当的直角坐标系,求出这条界线的方程.
[能力提升]
5.设双曲线C: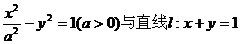 相交于两个不同的点A、B.求双曲线C的离心率e的取值范围。
相交于两个不同的点A、B.求双曲线C的离心率e的取值范围。
例6.(2006年北京宣武区)神舟6号飞船返回仓顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),B在A的正东方向,相距6km,C在B的北偏东30°,相距4km,P为航天员着陆点,某一时刻A接到P的求救信号,由于B、C两地比A距P远,因此4s后,B、C两个救援中心才同时接收到这一信号,已知该信号的传播速度为1km/s。
(I)求A、C两个救援中心的距离;
(II)求在A处发现P的方向角;
(III)若信号从P点的正上方Q点处发出,则A、B收到信号的时间差变大还是变小,说明理由。
[剖析]对于(1)以借助于两点间的距离公式得到;(2)抓住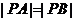 这一条件可知P在BC线段的垂直平分线上且
这一条件可知P在BC线段的垂直平分线上且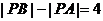 ,由双曲线的定义,可得P在以A、B为焦点的双曲线的左支上,从而求出其对应的方程;(3)是一个比较大小的问题,一般的处理思路是作差法比较.
,由双曲线的定义,可得P在以A、B为焦点的双曲线的左支上,从而求出其对应的方程;(3)是一个比较大小的问题,一般的处理思路是作差法比较.
[解]解:(I)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则
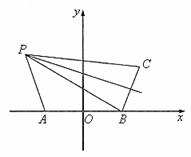
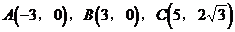
则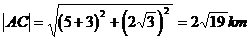
即A、C两个救援中心的距离为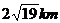
(II)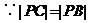 ,所以P在BC线段的垂直平分线上
,所以P在BC线段的垂直平分线上
又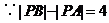 ,所以P在以A、B为焦点的双曲线的左支上,且
,所以P在以A、B为焦点的双曲线的左支上,且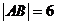
∴双曲线方程为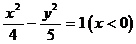
BC的垂直平分线的方程为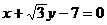 联立两方程解得:
联立两方程解得: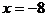
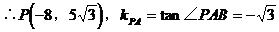 ∴∠PAB=120°
∴∠PAB=120°
所以P点在A点的北偏西30°处.
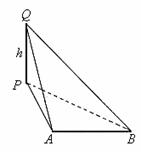
(III)如图,设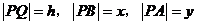
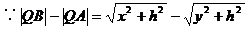
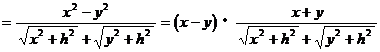
又∵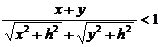 ,
,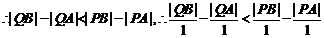
即A、B收到信号的时间差变小,且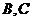 两救援中心收到信号的时间少于4秒。
两救援中心收到信号的时间少于4秒。
 [警示]面对实际问题,首先要构建数学模型,将实际问题转化为数学问题。本题抓住“A听到该巨响的时间比其它两测试点晚4s”想到差为定值,结合双曲线的定义,将实际问题转化为双曲线问题,进一步产生双曲线方程,从而顺利完成求解.从本题可以看出:抓住问题的本质促使转化是非常重要的一环.
[警示]面对实际问题,首先要构建数学模型,将实际问题转化为数学问题。本题抓住“A听到该巨响的时间比其它两测试点晚4s”想到差为定值,结合双曲线的定义,将实际问题转化为双曲线问题,进一步产生双曲线方程,从而顺利完成求解.从本题可以看出:抓住问题的本质促使转化是非常重要的一环.
[变式训练]
4.已知双曲线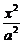 -
-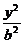 =1的离心率
=1的离心率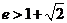 ,左、右焦点分别为F1、F2,左准线为l,能否在双曲线的左支上找一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?
,左、右焦点分别为F1、F2,左准线为l,能否在双曲线的左支上找一点P,使得|PF1|是P到l的距离d与|PF2|的等比中项?
例5.双曲线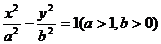 的焦距为2c,直线
的焦距为2c,直线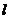 过点(a,0)和(0,b),且点(1,0)到直线
过点(a,0)和(0,b),且点(1,0)到直线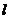 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线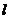 的距离之和
的距离之和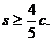 求双曲线的离心率e的取值范围.
求双曲线的离心率e的取值范围.
[剖析]本题是求双曲线的离心率取值范围问题,根据题设中的独立条件建立关于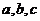 的等式或不等式,再利用
的等式或不等式,再利用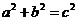 与
与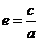 进行求解。
进行求解。
[解]直线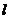 的方程为
的方程为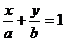 ,即
,即 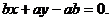
由点到直线的距离公式,且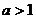 ,得到点(1,0)到直线
,得到点(1,0)到直线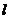 的距离
的距离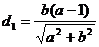 ,
,
同理得到点(-1,0)到直线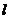 的距离
的距离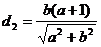
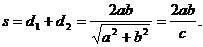
由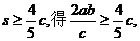 即
即 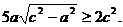
于是得 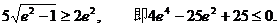
解不等式,得 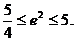
由于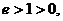 所以
所以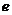 的取值范围是
的取值范围是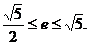
[警示]求方程的离心率的最值(或范围)问题,往往需要借僵双曲线的定义、图象、范围和性质,正(余)弦函数的有界性等,结合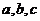 的关系,构造出一个关于离心率的不等式,从而达到求解的目的。
的关系,构造出一个关于离心率的不等式,从而达到求解的目的。
[变式训练]
3.已知双曲线关于两坐标轴对称,且与圆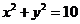 相交于点
相交于点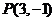 ,若此圆过点P的切线与双曲线的渐近线平行,求此双曲线的方程。
,若此圆过点P的切线与双曲线的渐近线平行,求此双曲线的方程。
例4.已知直线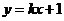 与双曲线
与双曲线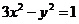 相交于A、B两点,那么是否存在实数
相交于A、B两点,那么是否存在实数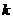 使得
使得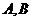 两点关于直线
两点关于直线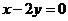 对称?若存在,求出
对称?若存在,求出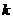 的值;若不存在,说明理由。
的值;若不存在,说明理由。
[剖析]这是一类非常典型的题目上,“已知曲线 :
: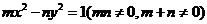 上是否存在相异的两点
上是否存在相异的两点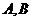 ,使
,使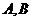 关于定直线
关于定直线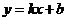 对称”这类问题的基本解决思路是:若存在
对称”这类问题的基本解决思路是:若存在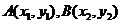 是曲线
是曲线 上相异两点,它们关于
上相异两点,它们关于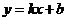 对称.设
对称.设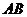 的中点为
的中点为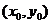 ,则
,则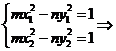
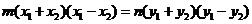 ,即
,即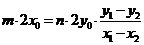 ,
,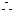
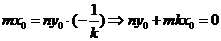 ①,又
①,又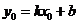 ②,由①②可解得
②,由①②可解得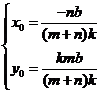 ,根据坐标
,根据坐标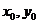 的范围,不难得出答案。
的范围,不难得出答案。
[解]设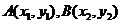 ,若存在这样的
,若存在这样的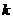 ,使
,使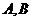 两点关于直线
两点关于直线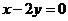 对称,则
对称,则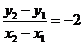 ,且
,且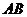 的中点
的中点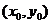 满足
满足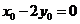 .由
.由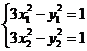 ,两式相减得:
,两式相减得:
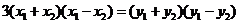 ,
,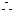
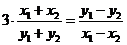 ,
,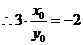 ,即
,即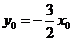 ,又
,又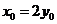 ,
,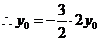 即
即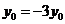 ,
,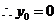 ,从而
,从而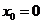 ,这显然是不可能的,故不存在这样的直线。
,这显然是不可能的,故不存在这样的直线。
[警示]对于类似的探索性题目,我们一般假设符合题设条件的直线存在,从这个假设出发,如果能够推导出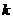 的值,则说明这样的直线是存在的;如果推导不出
的值,则说明这样的直线是存在的;如果推导不出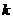 的值,或者说推导出矛盾的结果,这就说明满足条件的
的值,或者说推导出矛盾的结果,这就说明满足条件的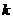 值不存在。
值不存在。
[变式训练]
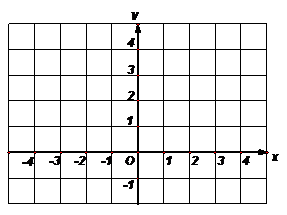
2.(2007年上海浦东)已知曲线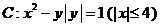 .
.
(1)画出曲线 的图像,
的图像,
(2)若直线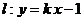 与曲线
与曲线 有两个公共点,求
有两个公共点,求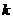 的取值范围;
的取值范围;
 (3)若
(3)若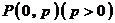 ,
,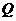 为曲线
为曲线 上的点,求
上的点,求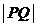 的最小值.
的最小值.
例3.已知双曲线C的中心在原点,焦点在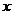 轴上,点
轴上,点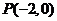 与其渐近线的距离为
与其渐近线的距离为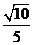 ,过点P作斜率为
,过点P作斜率为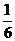 的直线交双曲线于
的直线交双曲线于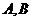 两点,交
两点,交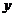 轴于M,且
轴于M,且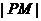 是
是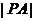 与
与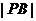 的等比中项.
的等比中项.
(1)求双曲线 的渐近线方程;
的渐近线方程;
(2)求双曲线 的方程.
的方程.
[剖析](1)由点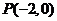 与其渐近线的距离为
与其渐近线的距离为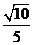 ,借助于点到直线的距离公式可求得其渐近线方程;(2)由渐近线方程,可设双曲线方程,再借助于题条件,不难得到双曲线方程。
,借助于点到直线的距离公式可求得其渐近线方程;(2)由渐近线方程,可设双曲线方程,再借助于题条件,不难得到双曲线方程。
[解](1)设双曲线的一条渐近线方程为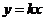 ,由点到直线的距离公式得
,由点到直线的距离公式得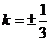 ,即双曲线的渐近线方程为
,即双曲线的渐近线方程为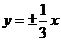 ;
;
(2)设双曲线方程为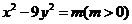 ,
,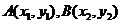 ,
,
则直线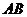 的方程为
的方程为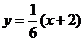 .由
.由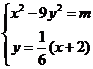 得
得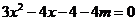 ,
,
当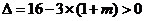 即
即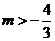 时,有
时,有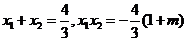
由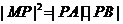 可得
可得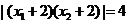 ,从而
,从而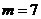 或
或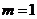 .
.
故所求的双曲线方程为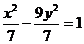 或
或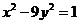 .
.
[警示]渐近线是双曲线特有的,如果说双曲线的方程为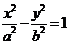 ,则其渐近线方程可记为
,则其渐近线方程可记为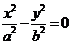 .同时,以
.同时,以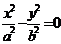 为渐近线的双曲线,其方程可设为
为渐近线的双曲线,其方程可设为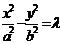 ;若已知双曲线的渐近线方程是以ax±by=0的形式给出的,则可设双曲线方程为a2x2-b2y2=
;若已知双曲线的渐近线方程是以ax±by=0的形式给出的,则可设双曲线方程为a2x2-b2y2=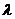 (
(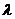 ≠0).
≠0).
[变式训练]
1. 根据下列条件,求双曲线方程:
(1)与双曲线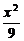 -
-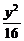 =1有共同的渐近线,且过点(-3,2
=1有共同的渐近线,且过点(-3,2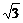 );
);
(2)与双曲线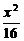 -
-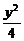 =1有公共焦点,且过点(3
=1有公共焦点,且过点(3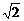 ,2).
,2).
例2.设点P到点M(-1,0)、N(1,0)距离之差为2m,到x轴、y轴距离之比为2,求m的取值范围.
[剖析]由|PM|-|PN|=2m,得||PM|-|PN||=2|m|.知点P的轨迹是双曲线,由点P到x轴、y轴距离之比为2,知点P的轨迹是直线,由交轨法求得点P的坐标,进而可求得m的取值 范围.
[解]设点P的坐标为(x,y),依题意得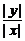 =2,即y=±2x(x≠0) ①
=2,即y=±2x(x≠0) ①
因此,点P(x,y)、M(-1,0)、N(1,0)三点不共线,得||PM|-|PN||<|MN|=2.
∵||PM|-|PN||=2|m|>0,∴0<|m|<1.因此,点P在以M、N为焦点,实轴长为2|m|的双曲线上.故设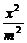 -
-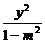 =1. ②
=1. ②
将①代入②,并解得x2=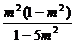 ,
,
∵1-m2>0,∴1-5m2>0.解得0<|m|<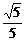 ,
,
即m的取值范围为(-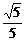 ,0)∪(0,
,0)∪(0,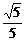 ).
).
[警示]求双曲线的方程,关键是求a、b,在解题过程中应熟悉各元素(a、b、c、e及准线)之间的关系,并注意方程思想的应用.
[变式训练]
6.给出问题:F1、F2是双曲线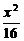 -
-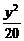 =1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
=1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面横线上;若不正确,将正确结果填在题中的横线上.______________________________________________________.
[典例精析]
例1.设双曲线与椭圆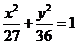 有共同的焦点,且与椭圆相交,一个交点的纵坐标为4,求双曲线的方程。
有共同的焦点,且与椭圆相交,一个交点的纵坐标为4,求双曲线的方程。
[剖析]由于椭圆的焦点坐标为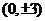 ,且双曲线与椭圆具有相同的焦点,知双曲线的焦点也为
,且双曲线与椭圆具有相同的焦点,知双曲线的焦点也为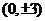 ,从而知所设双曲线的形式应为
,从而知所设双曲线的形式应为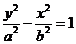 ,围绕定义产生的问题,要注意
,围绕定义产生的问题,要注意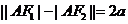 的三个量之间的关系。本题抓住“交点
的三个量之间的关系。本题抓住“交点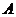 ”在双曲线上,必须满足定义,从而应用定义求出双曲线方程中的基本量。
”在双曲线上,必须满足定义,从而应用定义求出双曲线方程中的基本量。
[解]解法一:由椭圆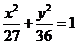 ,得其焦点为
,得其焦点为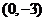 或
或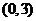 ,
, 双曲线的焦点在
双曲线的焦点在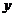 轴上,设所求的双曲线方程为
轴上,设所求的双曲线方程为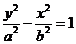 (
(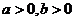 ). 由已知得双曲线两焦点分别为
). 由已知得双曲线两焦点分别为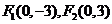 ,且与椭圆相交其中一个交点的纵坐标为4,设交点坐标为
,且与椭圆相交其中一个交点的纵坐标为4,设交点坐标为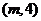 ,从而得
,从而得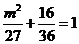 ,解得
,解得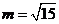 ,
,
则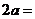
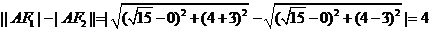
解得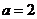 ,由于
,由于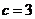 ,得
,得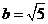 ,因此方程
,因此方程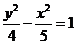 即为所求.
即为所求.
解法二:由题意设双曲线方程为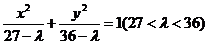 ,将A(
,将A(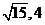 )代入求得
)代入求得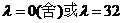 ,故所求双曲线方程为
,故所求双曲线方程为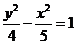 .
.
[警示]利用定义法来求解双曲线的标准方程时,一定要抓住题设所给出的独立条件建立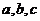 之间的等量关系,再利用
之间的等量关系,再利用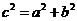 运用方程的思想来求解,从而得到
运用方程的思想来求解,从而得到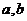 的值。但需注意首先应判断焦点的位置,以便于采用哪种形式的方程。
的值。但需注意首先应判断焦点的位置,以便于采用哪种形式的方程。
[变式训练]:
5.已知圆C过双曲线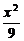 -
-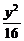 =1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是____________.
=1的一个顶点和一个焦点,且圆心在此双曲线上,则圆心到双曲线中心的距离是____________.
4.(2006年陕西卷)已知双曲线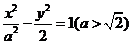 的两条渐近线的夹角为
的两条渐近线的夹角为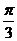 ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
(A)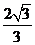 (B)
(B)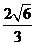 (C)
(C)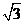 (D)2
(D)2
3.过点(2,-2)且与双曲线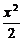 -y2=1有公共渐近线的双曲线方程是( )
-y2=1有公共渐近线的双曲线方程是( )
(A)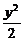 -
-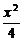 =1 (B)
=1 (B)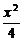 -
-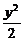 =1 (C)
=1 (C)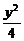 -
-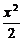 =1 (D)
=1 (D)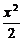 -
-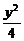 =1
=1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com