
2.(2006年山东卷)在给定椭圆中,过焦点且垂直于长轴的弦长为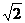 ,焦点到相应准线的距离为1,则该椭圆的离心率为 ( )
,焦点到相应准线的距离为1,则该椭圆的离心率为 ( )
(A)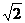 (B)
(B)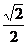 (C)
(C) 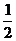 (D)
(D)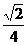
1.有以下两个命题:
(1)动点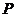 到两定点
到两定点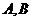 的距离之和
的距离之和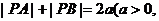 且
且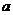 为常数);
为常数);
(2)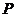 点的轨迹是椭圆.
点的轨迹是椭圆.
则命题(1)是命题(2)的( )
(A)必要不充分条件 (B)充分不必要条件 (C)充分且必要条件 (D)既不充分也不必要条件
6. 设F1、F2为椭圆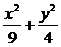 =1的两个焦点,P为椭圆上的一点.已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求
=1的两个焦点,P为椭圆上的一点.已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求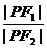 的值.
的值.
[能力提升]
5.设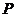 的轨迹是曲线
的轨迹是曲线 ,满足:点
,满足:点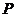 到
到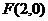 的距离与它到直线
的距离与它到直线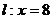 的距离之比是常数,又点
的距离之比是常数,又点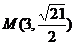 在曲线
在曲线 上,点
上,点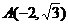 在曲线
在曲线 的内部.
的内部.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2) 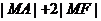 的最小值,并求此时点
的最小值,并求此时点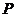 的坐标.
的坐标.
例6.设点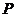 是椭圆
是椭圆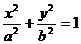 上一点,
上一点,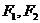 是椭圆的两个焦点,且
是椭圆的两个焦点,且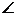
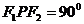 ,求椭圆的离心率的取值范围。
,求椭圆的离心率的取值范围。
[剖析]由题设条件不难看出
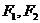 是一直角三角形的三个顶点,且由
是一直角三角形的三个顶点,且由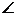
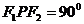 ,可想到利用勾股定理来加以解决。
,可想到利用勾股定理来加以解决。
[解]由椭圆的定义得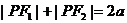 ①
①
在
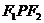 中,
中,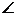
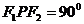 ,由勾股定理,得
,由勾股定理,得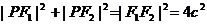 ②
②
将①②化简得: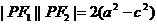 ③
③
由①③,根据韦达定理,可知 是方程
是方程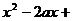
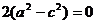 的两个根。
的两个根。
则有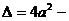
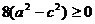 ,所以
,所以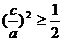 ,即
,即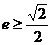 ,又
,又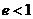 ,从而
,从而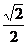
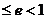 .
.
[警示] <<考试大纲>>要求掌握椭圆的简单几何性质,这就要求我们不仅准确把握和牢固地记忆这些几何性质,还要灵活地运用这些性质解决问题,更要注意教材中利用椭圆的标准方程推导这些几何性质的思想方法。在椭圆的几何性质中,离心率问题一直是高考的热点题型,需要重点把握。
[变式训练]
4.在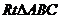 中,
中,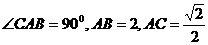 ,曲线E过C点,动点P在曲线E上运动,且保持
,曲线E过C点,动点P在曲线E上运动,且保持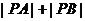 的值不变,求曲线E的方程。
的值不变,求曲线E的方程。
例5.设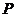 的轨迹是曲线
的轨迹是曲线 ,满足:点
,满足:点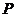 到
到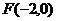 的距离与它到直线
的距离与它到直线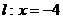 的距离之比是常数,又点
的距离之比是常数,又点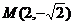 在曲线
在曲线 上,点
上,点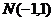 在曲线
在曲线 的内部.
的内部.
(1)求曲线 的方程;
的方程;
(2)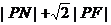 的最小值,并求此时点
的最小值,并求此时点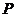 的坐标.
的坐标.
[剖析]:由已知条件通过列方程,不难得出曲线 的方程,但要注意计算准确。
的方程,但要注意计算准确。
[解](1)设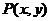 是曲线
是曲线 上任一点,则
上任一点,则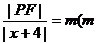 为常数),
为常数),
即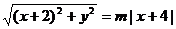 ,又点
,又点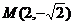 在曲线
在曲线 上,所以
上,所以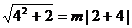 ,所以
,所以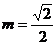 ,所以曲线
,所以曲线 的方程是
的方程是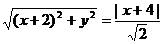 ,即
,即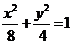 .
.
(2)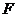 是椭圆
是椭圆 的左焦点,
的左焦点,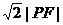 实际上是点
实际上是点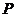 到左准线的距离.所以当
到左准线的距离.所以当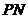 与左准线垂直时,
与左准线垂直时,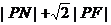 的值最小,此时点
的值最小,此时点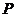 的坐标为
的坐标为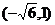 .
.
[警示]由本例可知,点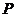 到
到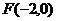 的距离与它到直线
的距离与它到直线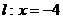 的距离之比
的距离之比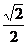 ,是一个在(0,1)的常数,事实上,平面内到一定点
,是一个在(0,1)的常数,事实上,平面内到一定点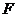 的距离和一条直线
的距离和一条直线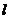 (
(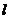 不在直线上)的距离之比是常数
不在直线上)的距离之比是常数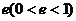 的动点的轨迹就是椭圆,其中定点
的动点的轨迹就是椭圆,其中定点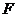 是椭圆的一个焦点,定直线
是椭圆的一个焦点,定直线 是椭圆的这个焦点所对应的准线,这就是椭圆的第二定义。
是椭圆的这个焦点所对应的准线,这就是椭圆的第二定义。
[变式训练]
3. 求满足下列各条件的椭圆的标准方程.
(1)焦点在坐标轴上,且经过两点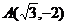 、
、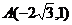 ;
;
(2)经过点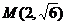 ,且与椭圆
,且与椭圆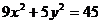 具有共同的焦点.
具有共同的焦点.
例4.在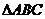 中,BC=24,AC、AB边上的中线长之和等于39,求
中,BC=24,AC、AB边上的中线长之和等于39,求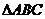 的重心的轨迹方程。
的重心的轨迹方程。
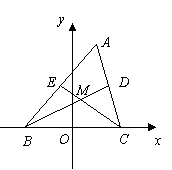 [剖析]:有一定长线段BC,两边上的中线长也均与定点B、C和
[剖析]:有一定长线段BC,两边上的中线长也均与定点B、C和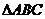 的重心有关,因此需考虑以BC的中点为坐标原点建立直角坐标系。但需注意点A不能在BC的所在的直线上。
的重心有关,因此需考虑以BC的中点为坐标原点建立直角坐标系。但需注意点A不能在BC的所在的直线上。
[解]如图所示,以线段BC所在直线为x轴、线段BC的中垂线为y轴建立直角坐标系。
设M为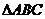 的重心,BD是AC边上的中线,CE是AB边上的中线,由重心的性质知
的重心,BD是AC边上的中线,CE是AB边上的中线,由重心的性质知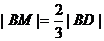 ,
,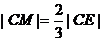 ,于是
,于是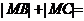
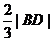
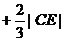 =
=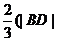
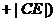 =
=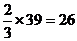 .根据椭圆的定义知,点M的轨迹是以B、C为焦点的椭圆.
.根据椭圆的定义知,点M的轨迹是以B、C为焦点的椭圆.
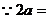
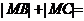 26,
26,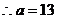 ,又
,又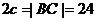 ,
,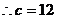 ,
,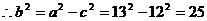 ,故所求的椭圆方程为
,故所求的椭圆方程为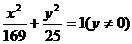 .
.
[警示] 在求点的轨迹时,要特点注意所求点轨迹的几何意义,在本题中,所求的椭圆方程为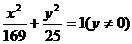 ,应考虑若
,应考虑若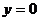 时,A、B、C三点在同一条直线上,不可能构成三角形,所以应将
时,A、B、C三点在同一条直线上,不可能构成三角形,所以应将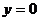 去掉。另外,平面内一动点与两定点F1,F2的距离之和为常数2a,当2a>| F1F2|时,动点的轨迹是椭圆;当2a=| F1F2|时动点的轨迹是线段F1F2;当2a<| F1F2|时,动点的轨迹不存在。
去掉。另外,平面内一动点与两定点F1,F2的距离之和为常数2a,当2a>| F1F2|时,动点的轨迹是椭圆;当2a=| F1F2|时动点的轨迹是线段F1F2;当2a<| F1F2|时,动点的轨迹不存在。
[变式训练]
2.(2006年江苏卷)已知三点P(5,2)、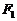 (-6,0)、
(-6,0)、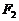 (6,0)。求以
(6,0)。求以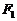 、
、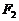 为焦点且过点P的椭圆的标准方程。
为焦点且过点P的椭圆的标准方程。
例3.求满足下列各条件的椭圆的标准方程.
(1)焦点在坐标轴上,且经过两点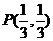 、
、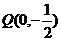 ;
;
(2)经过点(2,-3)且与椭圆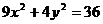 具有共同的焦点.
具有共同的焦点.
[剖析]对于(1),由题设条件不能确定椭圆的焦点在哪一坐标轴上,因此应分别设出焦点在x轴、y轴上的标准方程,进行讨论求解;或采用椭圆方程mx2+ny2=1(m>0,n>0,且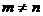 )直接求解,避免讨论;对于(2)由于椭圆
)直接求解,避免讨论;对于(2)由于椭圆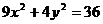 的焦点坐标为
的焦点坐标为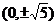 ,因而可设所求的椭圆方程为
,因而可设所求的椭圆方程为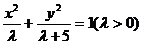 ,只要由题设条件确定
,只要由题设条件确定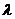 的值即可.
的值即可.
[解](1)[解法一]①当所求椭圆的焦点在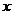 轴上时,设它的标准方程为
轴上时,设它的标准方程为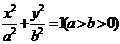 ,依题意应有
,依题意应有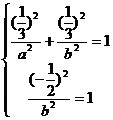 ,解得
,解得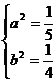 ,因为
,因为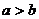 从而方程组无解;
从而方程组无解;
②当所求椭圆的焦点在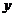 轴上时,设它的标准方程为
轴上时,设它的标准方程为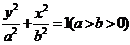 ,
,
依题意应有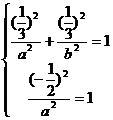 ,解得
,解得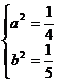 ,所以所求椭圆的标准方程为
,所以所求椭圆的标准方程为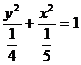 .
.
故所求的椭圆的标准方程为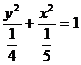
[解法二]设所求椭圆的方程为mx2+ny2=1(m>0,n>0,且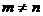 ),
),
依题意得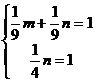 ,解得
,解得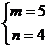 ,从而所求椭圆的标准方程为
,从而所求椭圆的标准方程为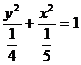 .
.
(2)[解]因为椭圆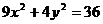 的焦点坐标为
的焦点坐标为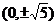 ,,从而可设所求的椭圆的方程为
,,从而可设所求的椭圆的方程为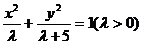 ,将又因为经过点(2,-3),从而得
,将又因为经过点(2,-3),从而得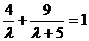 ,解得
,解得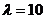 或
或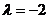 (舍去),故所求椭圆的标准方程为:
(舍去),故所求椭圆的标准方程为: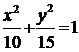 .
.
[警示]由于题(1)中的椭圆是唯一存在的,为了运算方便,可设其方程为mx2+ny2=1(m>0,n>0,且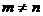 ),而不必考虑焦点的位置,求接求得椭圆的方程;题(2)中椭圆
),而不必考虑焦点的位置,求接求得椭圆的方程;题(2)中椭圆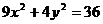 变形为
变形为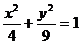 ,其焦点坐标为
,其焦点坐标为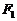
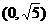 ,
,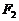
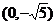 ,所设的方程
,所设的方程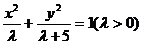 是具有共同焦点的
是具有共同焦点的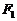
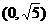 ,
,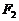
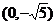 的椭圆系方程。遇到与本题类似的问题,我们可以采用类似的方法来求解椭圆的方程。另外本题还可以设方程
的椭圆系方程。遇到与本题类似的问题,我们可以采用类似的方法来求解椭圆的方程。另外本题还可以设方程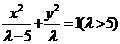 ,
,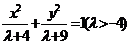 等解决。一般说来,与椭圆
等解决。一般说来,与椭圆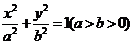 具有相同焦点的椭圆方程可设为
具有相同焦点的椭圆方程可设为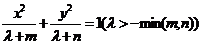 ,其中
,其中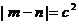 。本题实质上运用的也是待定系数法。
。本题实质上运用的也是待定系数法。
[变式训练]
1. 已知点A(3,0),B(-2,1)是椭圆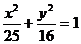 内的点,M是椭圆上的一动点,试求|MA|+|MB|的最大值与最小值。
内的点,M是椭圆上的一动点,试求|MA|+|MB|的最大值与最小值。
例2.已知点P在以坐标轴为对称轴的椭圆上,点P到两焦点的距离分别为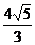 和
和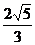 ,过点P作长轴的垂线,恰好过椭圆的一个焦点,求椭圆的方程。
,过点P作长轴的垂线,恰好过椭圆的一个焦点,求椭圆的方程。
[剖析]由题设条件设出椭圆的标准方程,求出焦距与长轴长是求解本题的关键。因椭圆的焦点位置未明确在哪个坐标轴上,故应有两种情况。
[解]设椭圆的两个焦点分别为F1,F2,|P F1|=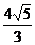 ,|P F2|=
,|P F2|=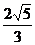
由椭圆的定义知2a=|P
F1|+|P F2|=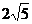 ,即
,即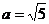 ,由|P F1|>|P F2|知P F2垂直于长轴。所以在
,由|P F1|>|P F2|知P F2垂直于长轴。所以在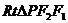 中,4c2=|P F1|2 -|P F2|2=
中,4c2=|P F1|2 -|P F2|2=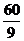 ,所以c2=
,所以c2=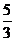 ,于是b2=a2-c2=
,于是b2=a2-c2=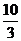
又由于所求的椭圆的焦点可以在x轴上,也可以在y轴上,故所求的椭圆方程为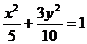 或
或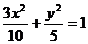 .
.
[警示]求椭圆的标准方程,需要一个定位条件和两个定形条件,通常采用待定系数法解决。椭圆中有“六点”(即两个交点与四个顶点)“四线”(即两条对称轴与两条准线),因此在解题时要注意它们对椭圆方程的影响,如在求椭圆的标准方程时,当遇到焦点位置不确定时,应注意有两种结果。
[变式训练]
6.短轴长为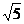 ,离心率
,离心率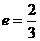 的椭圆的两焦点为F1,F2,过点F1作直线交椭圆于A、B两点,则
的椭圆的两焦点为F1,F2,过点F1作直线交椭圆于A、B两点,则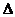 AB F2的周长是
.
AB F2的周长是
.
[典例精析]
例1.设F1,F2是椭圆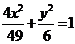 的两个焦点,P是椭圆上的点,且|P F1|:|P F2|=4:3,求
的两个焦点,P是椭圆上的点,且|P F1|:|P F2|=4:3,求 P F1F2的面积。
P F1F2的面积。
[剖析]由椭圆方程可求出2a与2c,且由|P F1|:|P F2|=4:3知可求出|P F1|,|P F2|的长度,从而可求三角形的面积。
[解]由于|P F1|+|P F2|=7,且|P F1|:|P F2|=4:3,得|P F1|=4,|P F2|=3,又| F1F2|=2c=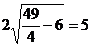 ,显然|P F1|2
+|P F2|2=| F1F2|2,所以
,显然|P F1|2
+|P F2|2=| F1F2|2,所以 P F1F2是以P F1,P F2为直角边的直角三角形,从而所求
P F1F2是以P F1,P F2为直角边的直角三角形,从而所求 P F1F2的面积为S=
P F1F2的面积为S=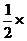 |P F1|
|P F1|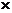 |P F2|=
|P F2|=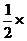 4
4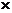 3=6.
3=6.
[警示]本题运用了椭圆的定义来解题。椭圆定义是用椭圆上任意一点P到两焦点的距离之和来描述的,定义中|P F1|+|P F2|=2a>| F1F2|.定义能够对一些距离进行相关的转化,简化解题过程。因此在解题过程中,遇到涉及椭圆上的点到焦点的距离问题时,应先考虑是否能够使椭圆的定义来解决。
[变式训练]:
5.(2006年上海卷)已知椭圆中心在原点,一个焦点为F(-2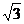 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 .
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com