
5.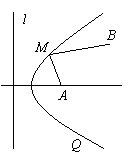 (2006年山东维坊高三统一考试)如图,南北方向的公路
(2006年山东维坊高三统一考试)如图,南北方向的公路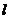 ,
,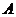 地在公路的正东方
地在公路的正东方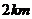 处,
处,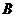 地在
地在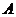 地东偏北
地东偏北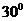 方向
方向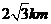 处,河流沿河岸
处,河流沿河岸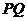 (曲线)上任一点到公路
(曲线)上任一点到公路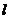 和到
和到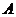 地距离相等。现要在曲线
地距离相等。现要在曲线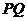 上选一处
上选一处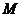 建一座码头,向
建一座码头,向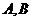 两地转运货物,经测算从
两地转运货物,经测算从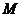 到
到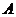 ,
,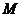 到
到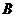 修建公路的费用均为
修建公路的费用均为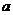 万元
万元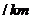 ,那么修建过两条公路的总费用最低是( )
,那么修建过两条公路的总费用最低是( )
(A)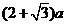 万元 (B)
万元 (B)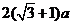 万元 (C)
万元 (C)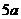 万元 (D)
万元 (D)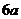 万元
万元
4.已知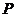 为抛物线
为抛物线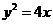 上任一动点,记点
上任一动点,记点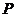 到
到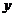 轴的距离为
轴的距离为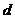 ,对于给定点
,对于给定点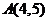 ,则
,则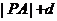 的最小值为( )
的最小值为( )
(A)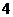 (B)
(B)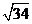 (C)
(C)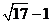 (D)
(D)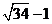
3.抛物线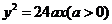 上有一点
上有一点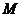 ,它的横坐标是3,它到焦点的距离为5,则抛物线的方程为( )
,它的横坐标是3,它到焦点的距离为5,则抛物线的方程为( )
(A)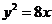 (B)
(B) 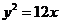 (C)
(C) 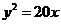 (D)
(D) 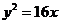
2.(2006年东北三校)已知点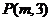 是抛物线
是抛物线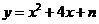 上距点
上距点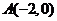 最近的点,则
最近的点,则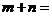 ( )
( )
(A)1 (B)3 (C)5 (D)7
1.(2006年山东泰安模拟试题)焦点坐标为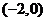 的抛物线的标准方程为( )
的抛物线的标准方程为( )
(A)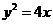 (B)
(B) 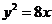 (C)
(C) 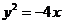 (D)
(D) 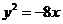
6.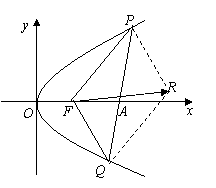 (2006年合肥模拟)如图,已知抛物线
(2006年合肥模拟)如图,已知抛物线 的方程为
的方程为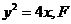 为抛物线的焦点,过点
为抛物线的焦点,过点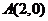 的直线
的直线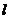 与抛物线
与抛物线 交于点
交于点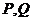 ,且
,且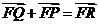 ,求点
,求点 的轨迹方程。
的轨迹方程。
[能力提升]
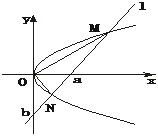
5.(2005年北京春季)如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b(a>0,b≠0),且交抛物线y2=2px(p>0)于M(x1,y1),N(x2,y2)两点.
|
例6.(2006年全国卷II)已知抛物线x2=4y的焦点为F,A、B是抛物线上的两动点,且=λ(λ>0).过A、B两点分别作抛物线的切线,设其交点为M.
(Ⅰ)证明·为定值;
(Ⅱ)设△ABM的面积为S,写出S=f(λ)的表达式,并求S的最小值.
[解] (Ⅰ)由已知条件,得F(0,1),λ>0.
设A(x1,y1),B(x2,y2).由=λ,即得 (-x1,1-y)=λ(x2,y2-1),
将①式两边平方并把y1=x12,y2=x22代入得y1=λ2y2 ③
解②、③式得y1=λ,y2=,且有x1x2=-λx22=-4λy2=-4,
抛物线方程为y=x2,求导得y′=x.
所以过抛物线上A、B两点的切线方程分别是y=x1(x-x1)+y1,y=x2(x-x2)+y2,
即y=x1x-x12,y=x2x-x22.
解出两条切线的交点M的坐标为(,)=(,-1).
所以·=(,-2)·(x2-x1,y2-y1)=(x22-x12)-2(x22-x12)=0
所以·为定值,其值为0.
(Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S=|AB||FM|.
|FM|===
==+.
因为|AF|、|BF|分别等于A、B到抛物线准线y=-1的距离,
所以|AB|=|AF|+|BF|=y1+y2+2=λ++2=(+)2.
于是S=|AB||FM|=(+)3,由+≥2知S≥4,且当λ=1时,S取得最小值4.
[警示]有向线段所成的比,线段的定比分点等概念,本身就是解析几何研究的一类重要问题。向量概念的引入,使这类问题的解决显得简洁而流畅。由于向量可以用一条有向线段来表示,有向线段的方向可以决定解析几何中直线的斜率,故直线的方向向量与解析几何中的直线有着天然的联系。求解此类问题的关键是:根据直线的方向向量得出直线方程,再转化为解析几何问题解决。求解这类问题可以用定比分点公式,也可以直接用有向线段的比解题。另外,向量的长度,点的平移等与解析几何都有着千丝万缕的联系,向量与解析几何的结合,为解决这些问题开辟了新的解题途径。
[变式训练]
4.设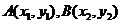 为抛物线
为抛物线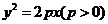 上位于
上位于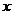 轴两侧的两点.
轴两侧的两点.
(1)若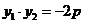 ,证明:直线
,证明:直线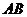 恒过一定点;
恒过一定点;
(2)若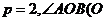 为坐标原点
为坐标原点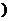 为钝角,求直线
为钝角,求直线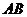 在
在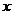 轴上的截距的取值范围.
轴上的截距的取值范围.
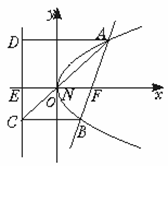
例5.设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴.证明直线AC经过原点O.
[剖析]证直线AC经过原点O,即证O、A、C三点共线,为此只需证kOC=kOA.本题也可结合图形特点,由抛物线的几何性质和平面几何知识去解决.
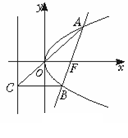 [解]解法一:设直线方程为y=k(x
[解]解法一:设直线方程为y=k(x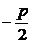 )A(x1,y1),B(x2,y2),C(
)A(x1,y1),B(x2,y2),C(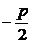 ,y2).
,y2).
∴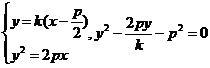 ,
,
∴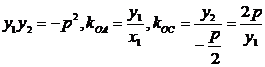 又∵y12=2px1 ∴kOC=
又∵y12=2px1 ∴kOC=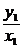 =kOA
=kOA
即k也是直线OA的斜率,所以AC经过原点O.
当k不存在时,AB⊥x轴,同理可得kOA=kOC,所以AC经过原点O.
解法二:因为抛物线y2=2px(p>0)的焦点为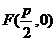 ,由于直线
,由于直线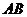 斜率不为0,所以经过点
斜率不为0,所以经过点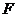 的直线
的直线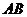 的方程可设为
的方程可设为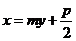 ,代入抛物线方程消去
,代入抛物线方程消去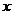 得
得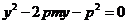 .若记
.若记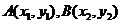 ,则
,则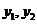 是该方程的两个根,所以
是该方程的两个根,所以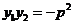 ,因为
,因为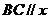 轴,且点
轴,且点 在准线
在准线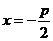 上,所以点
上,所以点 的坐标
的坐标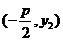 ,
,
 故直线
故直线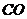 的斜率为
的斜率为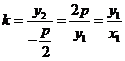 ,
,
即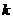 也是直线
也是直线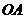 的斜率,所以直线
的斜率,所以直线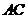 经过原点
经过原点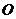 .
.
解法三:如图,过A作AD⊥l,D为垂足,则:AD∥EF∥BC
连结AC与EF相交于点N,
则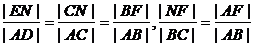
由抛物线的定义可知:|AF|=|AD|,|BF|=|BC|
∴|EN|=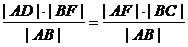 =|NF|.
=|NF|.
即点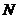 是
是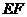 的中点,与抛物线的顶点
的中点,与抛物线的顶点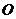 重合,所以直线
重合,所以直线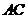 经过原点
经过原点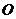 .
.
[警示]本例实际揭示了抛物线焦点弦的一个几何性质“A、O、C三点共线”.其中证法一采用常规的坐标法,借助代数推理进行,解题思路容易找到,但容易漏解;证法二中将直线设为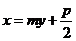 有两个好处:一是它包括了
有两个好处:一是它包括了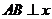 轴的情形,避免了将直线
轴的情形,避免了将直线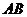 的斜率作为参数时对
的斜率作为参数时对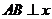 轴情况的讨论;二是可以直接求得
轴情况的讨论;二是可以直接求得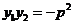 ;证法三采用圆锥曲线的几何性质,借助平面几何的方法进行推理,体现了数与形的结合.解题思路宽,而且几何方法较之解析法比较快捷便当.从审题与思维深度上看,几何法的采用,源于思维的深刻.另外,本题也可以采用平面向量加以证明,同学们可以试一下.
;证法三采用圆锥曲线的几何性质,借助平面几何的方法进行推理,体现了数与形的结合.解题思路宽,而且几何方法较之解析法比较快捷便当.从审题与思维深度上看,几何法的采用,源于思维的深刻.另外,本题也可以采用平面向量加以证明,同学们可以试一下.
[变式训练]
3. 已知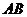 为抛物线
为抛物线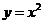 的动弦,且
的动弦,且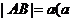 为常数且
为常数且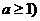 ,求弦
,求弦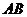 的中点
的中点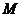 离
离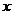 轴的最近距离.
轴的最近距离.
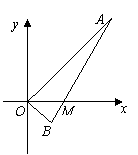
例4.如图所示,线段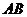 过
过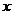 轴正半轴上一定点
轴正半轴上一定点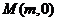 ,端点
,端点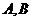 到
到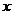 轴的距离之积为
轴的距离之积为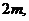 以
以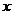 轴为对称轴,过
轴为对称轴,过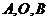 三点作抛物线。
三点作抛物线。
(1)求抛物线的方程;
(2)若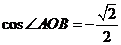 ,求
,求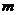 的取值范围.
的取值范围.
[剖析]此题目利可将直线方程与抛物线的方程联立,消去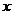 后利用韦达定理,求得抛物线方程;在考虑角度问题时一般利用余弦定理。
后利用韦达定理,求得抛物线方程;在考虑角度问题时一般利用余弦定理。
[解](1)由题意设抛物线的方程为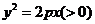 ,直线
,直线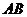 的方程为
的方程为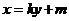 ,
,
由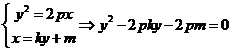 ,由韦达定理得
,由韦达定理得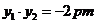
由已知条件知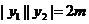 ,从而
,从而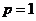 ,故抛物线方程为
,故抛物线方程为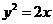 .
.
(2)由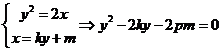 ,设
,设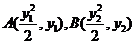
由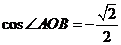 ,得
,得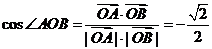
即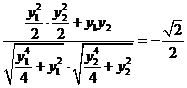 ,化简得
,化简得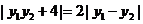
因为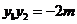 且
且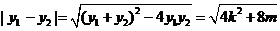 ,
,
即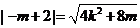 ,
,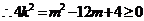 ,解得:
,解得: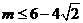 或
或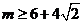 (舍)
(舍)
故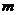 的取值范围为
的取值范围为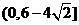
[警示](1)涉及几何性质的问题往往要结合图形来进行思考,通过图形可以看出抛物线的顶点、对称轴、开口方向等.
(2)对解题过程进行完备性思考是必要的,这样可以有效地避免错误,本题若缺少这种思考,很容易误认为答案就是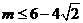 或
或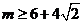 ,其实当
,其实当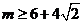 时,
时,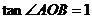 ,并非是
,并非是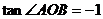 .
.
(3)本题若将直线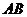 的方程设为点斜式,则需要讨论
的方程设为点斜式,则需要讨论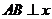 轴的情形.
轴的情形.
[变式训练]
2.求满足下列条件的抛物线方程
(1)抛物线的顶点在原点,对称轴为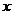 轴,抛物线上一点
轴,抛物线上一点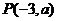 到焦点的距离为5;
到焦点的距离为5;
(2)以原点为顶点,从坐标轴为对称轴,并且经过点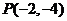 .
.
例3.设点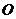 为抛物线的顶点,
为抛物线的顶点,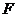 是抛物线的焦点且
是抛物线的焦点且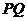 为过焦点的弦,若
为过焦点的弦,若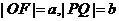 ,求
,求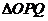 的面积.
的面积.
[剖析]本题将焦点弦分成两段,利用定义将焦点弦长用两端点横坐标表示,结合方程,通过韦达定理产生问题的结论。另外,将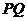 所在直线方程设为
所在直线方程设为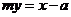 ,这样可以避免斜率存在与否的讨论.
,这样可以避免斜率存在与否的讨论.
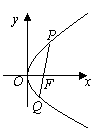 [解]取
[解]取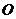 为坐标原点,
为坐标原点,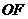 所在的直线为
所在的直线为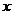 轴,建立如图所示的直角坐标系,
轴,建立如图所示的直角坐标系,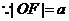 ,
,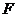 为焦点,
为焦点,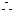 抛物线方程为
抛物线方程为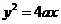 .
.
设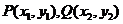 ,
,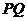 所在的直线为
所在的直线为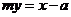 .
.
由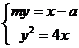 得
得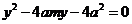 ,则
,则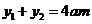
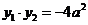 .由抛物线的定义,焦点弦长
.由抛物线的定义,焦点弦长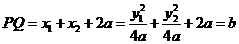
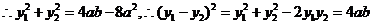
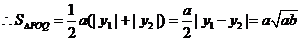 .
.
[警示]若直线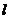 交抛物线
交抛物线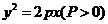 于
于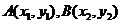 两点,交
两点,交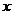 轴于
轴于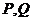 ,
,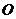 为坐标原点,则三角形
为坐标原点,则三角形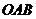 的面积为
的面积为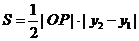 .
.
[变式训练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com