
5. 4名男生5名女生,一共9名实习生分配到高一的四个班级担任见习班主任,每班至少有男、女实习生各1名的不同分配方案共有多少种?
4.一个五棱柱的任意两个侧面都不平行,且底面内的任意一条对角线与另一底面的边也不平行,以它的顶点为顶点的四面体有多少个?
3.有5双不同型号的皮鞋,从中任取4只有多少种不同的取法?所取的4只中没有2只是同型号的取法有多少种?所取的4只中有一双是同型号的取法有多少种?
2. 在7名运动员中选出4人组成接力队,参加4×100米接力赛,那么甲、乙两人都不跑中间两棒的安排方法有多少种?
1.某一天的课程表要排入语文、数学、英语、物理、体育、音乐6节课,如果第一节不排体育,最后一节不排数学,一共有多少种不同的排法?
[例1] 10个人走进只有6把不同椅子的屋子,若每把椅子必须且只能坐一人,共有多少种不同的坐法?
错解:10个人坐6把不同的椅子,相当于10个元素到6个元素的映射,故有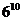 种不同的坐法.
种不同的坐法.
错因: 没弄清题意,题中要求每把椅子必须并且只能坐一人,已不符合映射模型了.本题事实上是一个排列问题.
正解: 坐在椅子上的6个人是走进屋子的10个人中的任意6个人,若把人抽象地看成元素,将6把不同的椅子当成不同的位置,则原问题抽象为从10个元素中作取6个元素占据6个不同的位置.显然是从10个元素中任取6个元素的排列问题.从而,共有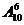 =151200种坐法.
=151200种坐法.
[例2]从-3,-2,-1,0,1,2,3,4八个数字中任取3个不同的数字作为二次函数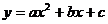 的系数
的系数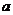 ,b,c的取值,问共能组成多少个不同的二次函数?
,b,c的取值,问共能组成多少个不同的二次函数?
错解:从八个数字中任取3个不同的数字作为二次函数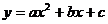 的系数
的系数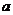 ,b,c的取值,交换
,b,c的取值,交换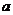 ,b,c的具体取值,得到的二次函数就不同,因而本题是个排列问题,故能组成
,b,c的具体取值,得到的二次函数就不同,因而本题是个排列问题,故能组成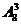 个不同的二次函数.
个不同的二次函数.
错因: 忽视了二次函数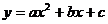 的二次项系数
的二次项系数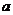 不能为零.
不能为零.
正解: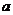 ,b,c中不含0时,有
,b,c中不含0时,有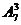 个;
个;
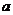 ,b,c中含有0时,有2
,b,c中含有0时,有2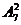 个.
个.
故共有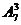 +2
+2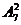 =294个不同的二次函数.
=294个不同的二次函数.
注:本题也可用间接解法.共可构成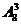 个函数,其中
个函数,其中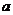 =0时有
=0时有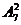 个均不符合要求,从而共有
个均不符合要求,从而共有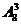 -
-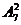 =294个不同的二次函数.
=294个不同的二次函数.
[例3]以三棱柱的顶点为顶点共可组成多少个不同的三棱锥?
错解:按照上底面取出点的个数分三类:第一类,上底面恰取一点,这时下底面取三点,有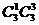 =3个;第二类,上底面恰取2点,下底面也取两点,有
=3个;第二类,上底面恰取2点,下底面也取两点,有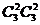 =9个;上底面取3点时,下底面取一点,有
=9个;上底面取3点时,下底面取一点,有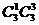 =3个.综上知,共可组成3+9+3=15个不同的三棱锥.
=3个.综上知,共可组成3+9+3=15个不同的三棱锥.
错因: 在上述解法中,第二类情形时,所取四点有可能共面.这时,务必注意在上底面取2点,与之对应的下底面的2点只有2种取法.
正解:在三棱柱的六个顶点中任取4个顶点有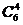 =15取法,其中侧面上的四点不能构成三棱锥,故有15-3=12个不同的三棱锥.
=15取法,其中侧面上的四点不能构成三棱锥,故有15-3=12个不同的三棱锥.
[例4] 4名男生和3名女生并坐一排,分别回答下列问题:
(1)男生必须排在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)男生相邻、女生也相邻的坐法有多少种?
(4)男女生相间的坐法有多少种?
(5)女生顺序已定的坐法有多少种?
解:⑴从整体出发,视四名男生为一整体,看成一个“大元素”,与三名女生共四个元素进行排列,有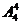 种坐法;而大元素内部的小元素间又有
种坐法;而大元素内部的小元素间又有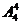 种坐法.故共有
种坐法.故共有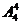
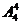 =576种坐法.
=576种坐法.
⑵因为女生 互不相邻,故先将4名男生排好,有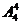 种排法;然后在男生之间及其首尾的5个空档中插入3名女生,有
种排法;然后在男生之间及其首尾的5个空档中插入3名女生,有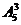 种排法.故共有
种排法.故共有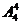
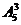 =1440种排法.
=1440种排法.
⑶类似(1)可得: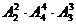 =288种
=288种
⑷男生排好后,要保证男生互不相邻、女生也互不相邻,3名女生只能排在男生之间的3个空档中,有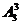 种排法.故共有
种排法.故共有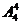
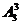 =144种排法.
=144种排法.
⑸7个元素的全排列有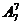 种,因为女生定序,而她们的顺序不固定时有
种,因为女生定序,而她们的顺序不固定时有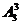 排法,可知
排法,可知
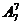 中重复了
中重复了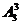 次,故共有
次,故共有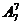 ÷
÷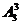 =
=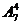 =840种排法.
=840种排法.
本题还可这样考虑:让男生先占7个位置中的4个,共有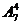 种排法;余下的位置排女生,因为女生定序,故她们只有1排法,从而共有
种排法;余下的位置排女生,因为女生定序,故她们只有1排法,从而共有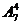 =840种排法.
=840种排法.
[例5] 某运输公司有7个车队,每个车队的车均多于4辆,现从这个车队中抽调出10辆车,并且每个车队至少抽调一辆,那么共有多少种不同的抽调方法?
解:在每个车队抽调一辆车的基础上,还须抽调的3辆车可分成三类:从一个车队中抽调,有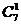 =7种;从两个车队中抽调,一个车队抽1辆,另一个车队抽两辆,有
=7种;从两个车队中抽调,一个车队抽1辆,另一个车队抽两辆,有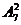 =42种;从三个车队中抽调,每个车队抽调一辆,有
=42种;从三个车队中抽调,每个车队抽调一辆,有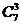 =35辆.由分类计数原理知,共有7+42+35=84种抽调方法.
=35辆.由分类计数原理知,共有7+42+35=84种抽调方法.
本题可用档板法来解决:由于每个车队的车均多于4辆,只需将10个份额分成7份.具体来讲,相当于将10个相同的小球,放在7个不同的盒子中,且每个盒子均不空.可将10个小球排成一排,在相互之间的九个空档中插入6个档板,即可将小球分成7份,因而有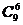 =84种抽调方法.
=84种抽调方法.
[例6]用0,1,2,…,9这十个数字组成无重复数字的四位数,若千位数字与个位数字之差的绝对值是2,则这样的四位数共有多少个?
解:若千位数字与个位数字中有一个为0 ,则另一个为2,且0只能在个位,2在千位,这样有四位数有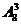 个.若千位与个位都不含有0,则应为1与3、2与4,3与5、4与6,5与7、6与8,7与9,这样的四位数有7×
个.若千位与个位都不含有0,则应为1与3、2与4,3与5、4与6,5与7、6与8,7与9,这样的四位数有7×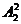 ×
×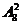 个.
个.
∴共有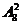 +7
+7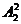 ×
×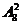 =840个符合条件的四位数
=840个符合条件的四位数
6.解排列与组合应用题时,首先应抓住是排列问题还是组合问题.界定排列与组合问题是排列还是组合,唯一的标准是“顺序”,有序是排列问题,无序是组合问题.当排列与组合问题综合到一起时,一般采用先考虑组合后考虑排列的方法解答.其次要搞清需要分类,还是需要分步.分类计数原理与分步计数原理是关于计数的两个基本原理,它们不仅是推导排列数公式和组合数公式的基础,而且其应用贯穿于排列与组合的始终.学好两个计数原理是解决排列与组合应用题的基础.切记:排组分清(有序排列、无序组合),加乘明确(分类为加、分步为乘).
5.排列与组合的区别与联系:
①根据排列与组合的定义,前者是从n个不同元素中取出m个不同元素后,还要按照一定的顺序排成一列,而后者只要从n个不同元素中取出m个不同元素并成一组,所以区分某一问题是排列还是组合问题,关键看选出的元素与顺序是否有关,若交换某两个元素的位置对结果产生影响,则是排列问题,而交换任意两个元素的位置对结果没有影响,则是组合问题.也就是说排列与选取元素的顺序有关,组合与选取元素的顺序无关.
②排列与组合的共同点,就是都要“从n个不同元素中,任取m(m≤n)个元素”,而不同点在于元素取出以后,是“排成一排”,还是“组成一组”,其实质就是取出的元素是否存在顺序上的差异.因此,区分排列问题和组合问题的主要标志是:是否与元素的排列顺序有关,有顺序的是排列问题,无顺序的组合问题.例如123和321,132是不同的排列,但它们都是相同的组合.再如两人互寄一次信是排列问题,互握一次手则是组合问题.
③排列数与组合数的联系.求从n个不同元素中取出m个元素的排列数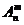 ,可以分为以下两步:第一步,先求出从这n个不同元素中取出m个元素的组合数
,可以分为以下两步:第一步,先求出从这n个不同元素中取出m个元素的组合数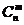 ;第二步,求每一个组合中m个元素的全排列数
;第二步,求每一个组合中m个元素的全排列数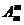 .根据分步计数原理,得到
.根据分步计数原理,得到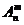 =
=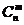
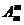 .从这一过程中可得出排列与组合的另一重要联系.从而,在解决排列问题时,先取后排是一个常见的解题策略.
.从这一过程中可得出排列与组合的另一重要联系.从而,在解决排列问题时,先取后排是一个常见的解题策略.
4.对组合的理解:如果两个组合中的元素完全相同,那么不管它们顺序如何都是相同的组合.当两个组合中的元素不完全相同时(即使只有一个元素不同),就是不同的组合.
3.排列应用题一般分为两类,即无限制条件的排列问题和有限制条件的排列问题.常见题型有:排队问题、数字问题、与几何有关的问题.
解排列应用题时应注意以下几点:
①认真审题,根据题意分析它属于什么数学问题,题目中的事件是什么,有无限制条件,通过怎样的程序完成这个事件,用什么计算方法.
②弄清问题的限制条件,注意研究问题,确定特殊元素和特殊的位置.考虑问题的原则是特殊元素、特殊位置优先,必要时可通过试验、画图、小数字简化等手段帮助思考.
③恰当分类,合理分步.
④在分析题意,画框图来处理,比较直观.在解应用时,应充分运用.
解排列应用题的基本思路:
①基本思路:
直接法:即从条件出发,直接考虑符合条件的排列数;
间接法:即先不考虑限制条件,求出所有排列数,然后再从中减去不符合条件的排列数.
②常用方法:特殊元素、特殊位置分析法,排除法(也称去杂法),对称分析法,捆绑法,插空档法,构造法等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com