
5.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?
4. 在连结正八边形的三个顶点组成的三角形中,与正八边形有公共边的有多少个?
3. 在1,2,3,4,7,9中任取不相同的两个数,分别作为对数的底数与真数,能得到多少个不同的对数值?
2.集合A={1,2,-3},B={-1,-2,3,4},从A、B中各取1个元素作为占点P的坐标.(1)可以得到多少个不同的点?
(2)在这些点中位于第一象限的点有几个?
1.将4个不同的小球放入编号为1、2、3的三个不同的盒子中,其中每个盒子都不空的放法共有( )
A.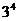 种
B.
种
B.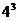 种
C.18种 D.36种
种
C.18种 D.36种
[例1]体育场南侧有4个大门,北侧有3个大门,某学生到该体育场练跑步,则他进出门的方案有 ( )
A.12 种 B.7种 C.24种 D.49种
错解:学生进出体育场大门需分两类,一类从北边的4个门进,一类从南侧的3个门进,由分类计数原理,共有7种方案. ∴选B
错因:没有审清题意.本题不仅要考虑从哪个门进,还需考虑从哪个门出,应该用分步计数原理去解题.
正解:学生进门有7种选择,同样出门也有7种选择,由分步计数原理,该学生的进出门方案有7×7=49种. ∴应选D.
[例2]从1,2,3,…,10中选出3个不同的数,使这三个数构成等差数列,则这样的数列共有多少个?
错解:根据构成的等差数列的公差,分为公差为1、2、3、4四类.公差为1时,有8个;公差为2时,首先将数字分成1,3,5,7,9,和2,4,6,8,10两组,再得到满足要求的数列共3+3=6个;公差为3时,有1,4,7和4,7,10和3,6,9以及2,5,8,共4个;公差为4时,只有1,5,9和2,6,10两个.由分类计数原理可知,共构成了不同的等差数列8+6+4+2=20个.
错因:上述解答忽略了1,2,3与3,2,1它们是不同的数列, 因而导致考虑问题不全面,从而出现漏解. 这需要在解题过程中要全方位、多角度审视问题.
正解:根据构成的等差数列的公差,分为公差为±1、±2、±3、±4四类.公差为±1时,有8×2=16个;公差为±2时,满足要求的数列共6×2=12个;公差为±3时,有4×2=8个;公差为±4时,只有2×2=4个.由分类计数原理可知,共构成了不同的等差数列16+12+8+4=40个.
[例3]三张卡片的正反面分别写有1和2,3和4,5和6,若将三张卡片并列,可得到几个不同的三位数(6不能作9用).
解:解法一 第一步,选数字.每张卡片有两个数字供选择,故选出3个数字,共有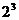 =8种选法.第二步,排数字.要排好一个三位数,又要分三步,首先排百位,有3种选择,由于排出的三位数各位上的数字不可能相同,因而排十位时有2种选择,排个位只有一种选择.故能排出3×2×1=6个不同的三位数.
=8种选法.第二步,排数字.要排好一个三位数,又要分三步,首先排百位,有3种选择,由于排出的三位数各位上的数字不可能相同,因而排十位时有2种选择,排个位只有一种选择.故能排出3×2×1=6个不同的三位数.
由分步计数原理,共可得到8×6=48个不同的三位数.
解法二:第一步,排百位有6种选择,
第二步,排十位有4种选择,
第三步,排个位有2种选择.
根据分步计数原理,共可得到6×4×2=48个不同的三位数.
注:如果6能当作9用,解法1仍可行.
[例4]集合A={1,2,3,4},集合B={-1,-2},可建立多少个以A为定义域B为值域的不同函数?
分析:函数是特殊的映射,可建立映射模型解决.
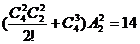 解: 从集合A到集合B的映射共有
解: 从集合A到集合B的映射共有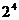 =16个,只有都与-1,或-2对映的两个映射不符合题意,故以A为定义域B为值域的不同函数共有16-2=14个.
=16个,只有都与-1,或-2对映的两个映射不符合题意,故以A为定义域B为值域的不同函数共有16-2=14个.
或
[例5] 用0,1,2,3,4,5这六个数字,
(1)可以组成多少个数字不重复的三位数?
(2)可以组成多少个数字允许重复的三位数?
(3)可以组成多少个数字不重复的三位奇数?
(4)可以组成多少个数字不重复的小于1000的自然数?
(5)可以组成多少个数字不重复的大于3000,小于5421的四位数?
解:(1)分三步:①先选百位数字,由于0不能作为百位数,因此有5种选法;②十位数字有5种选法;③个位数字有4种选法.由分步计数原理知所求三位数共有5×5×4=100个.
(2)分三步:①先选百位数字,由于0不能作为百位数,因此有5种选法;②十位数字有6种选法;③个位数字有6种选法.由分步计数原理知所求三位数共有5×6×6=180个.
(3)分三步:①先选个位数字,由于组成的三位数是奇数,因此有3种选法;②再选百位数字有4种选法;③个位数字也有4种选法.由分步计数原理知所求三位数共有3×4×4=48个.
(4)分三类:①一位数,共有6个;②两位数,共有5×5=25个;③三位数,共有5×5×4=100个.因此,比1000小的自然数共有6+25+100=131个
(5)分四类:①千位数字为3,4之一时,共有2×5×4×3=120个;②千位数字为5,百位数字为0,1,2,3之一时,共有4×4×3=48个;③千位数字为5,百位数字是4,十位数字为0,1之一时,共有2×3=6个;④还有5420也是满足条件的1个.故所求自然数共120+48+6+1=175个
评注:排数字问题是最常见的一种题型,要特别注意首位不能排0.
5.在有些问题中,还应充分注意到在完成某件事时,具体实践的可行性.例如:从甲地到乙地 ,要从甲地先乘火车到丙地,再从丙地乘汽车到乙地.那么从甲地到乙地共有多少种不同的走法?这个问题中,必须注意到发车时刻,所限时间,答案较多.
4.在具体解题时,常常见到某个问题中,完成某件事,既有分类,又有分步,仅用一种原理不能解决,这时需要认真分析题意,分清主次,选择其一作为主线.
3.两个原理的区别在于一个和分类有关,一个和分步有关.如果完成一件事有n类办法,这n类办法彼此之间是相互独立的,无论哪一类办法中的哪一个都能单独完成这件事,求完成这件事的方法种数,就用分类计数原理.如果完成一件事,需分成n个步骤,缺一不可,即需要依次完成所有的步骤,才能完成这件事,完成每一个步骤各有若干种不同的方法,求完成这件事的方法种数,就用分步计数原理.
2.分步原理中分步的理解:“完成一件事,需要分成n个步骤”这就是说完成这件事的任何一种方法,都要完成这n个步骤.分步时,首先要根据问题的特点确定一个可行的分步标准,其次,步骤的设置要满足完成这件事必须并且只需连续完成这n个步骤,这件事才算最终完成.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com