
5.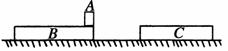 (04全国卷Ⅳ25)如图所示,在一光滑的水平面上有两块相同的木板B和C.重物A(视为质点)位于B的右端,A、B、C的质量相等.现A和B以同一速度滑向静止的C,B与C发生正碰.碰后B和C粘在一起运动,A在C上滑行,A与C有摩擦力.已知A滑到C的右端而未掉下.试问:
(04全国卷Ⅳ25)如图所示,在一光滑的水平面上有两块相同的木板B和C.重物A(视为质点)位于B的右端,A、B、C的质量相等.现A和B以同一速度滑向静止的C,B与C发生正碰.碰后B和C粘在一起运动,A在C上滑行,A与C有摩擦力.已知A滑到C的右端而未掉下.试问:
B、C发生正碰到A刚移动到C右端期间,C所走过的距离是C板长
度的多少倍?
答案 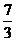 倍
倍
解析 设A、B、C的质量均为m.碰撞前,A与B的共同速度为v0,碰撞后B与C的共同速度为v1。对B、C,由动量守恒定律得 mv0=2mv1 ①
设A滑至C的右端时,三者的共同速度为v2.对A、B、C,由动量守恒定律得
2mv0=3mv1 ②
设A与C的动摩擦因数为μ,从发生碰撞到A移至C的右端时C所走过的距离为S.对B、C由功能关系
μ(2m)gs= (2m)v22-
(2m)v22- (2m)v12 ③
(2m)v12 ③
Μmg(s+l)=  mv02-
mv02- mv22 ④
mv22 ④
由以上各式解得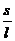 =
=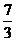
4.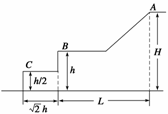 (04上海21)滑雪者从A点由静止沿斜面滑下,经一平台后水平飞离B点,
(04上海21)滑雪者从A点由静止沿斜面滑下,经一平台后水平飞离B点,
地面上紧靠平台有一个水平台阶,空间几何尺度如图所示.斜面、平台与滑雪
板之间的动摩擦因数均为μ.假设滑雪者由斜面底端进入平台后立即沿水平方
向运动,且速度大小不变.求:
(1)滑雪者离开B点时的速度大小;
(2)滑雪者从B点开始做平抛运动的水平距离s.
答案 (1)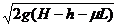
(2)当H-μL<2h时,s=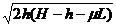 当H-μL>2h时,s=2
当H-μL>2h时,s=2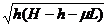
解析 (1)设滑雪者质量为m,斜面与水平面间的夹角为θ,滑雪者滑行过程中克服摩擦力做功W=μmgs?cosθ+μmg(L-scosθ)=μmgL
由动能定理mg(H-h)-μmgL= mv2
mv2
离开B点时的速度v=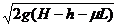
(2)设滑雪者离开B点后落在台阶上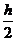 =
= gt12,s1=vt1<
gt12,s1=vt1<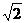 h
h
可解得s1=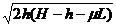 <
<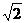 h
h
此时必须满足H-μL<2h.
当H-μL>2h时,滑雪者直接落到地面上.h= gt22,s=vt2
gt22,s=vt2
可解得s=2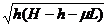
3.(04广东14)一质量为m的小球,以初速度v0沿水平方向射出,恰好垂直地射到一倾角为30°的固定斜面上,并立即沿反方向弹回.已知反弹速度的大小是入射速度大小的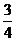 ,求在碰撞过程中斜面对小球的冲量大小.
,求在碰撞过程中斜面对小球的冲量大小.
答案 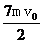
解析 令小球与斜面相碰时速度大小为v,由题意可知,碰后的速度大小为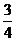 v,因小球与斜面垂直相碰撞,后被反弹回,则碰撞中斜面对小球的冲量大小为I,(设定反弹回的速度方向为正)由动量定理得:
v,因小球与斜面垂直相碰撞,后被反弹回,则碰撞中斜面对小球的冲量大小为I,(设定反弹回的速度方向为正)由动量定理得:
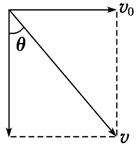 I=Δp=m×
I=Δp=m×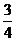 v-(-mv)=
v-(-mv)=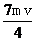
又因小球水平的初速度为v0,由右图可得:v=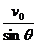 =2v0
=2v0
所以碰撞中斜面对小球的冲量大小为:I=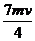 =
=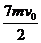
2.(05北京春招24)下雪天,卡车在笔直的高速公路上匀速行驶.司机突然发现前方停着一辆故障车,他将刹车踩到底,车轮被抱死,但卡车仍向前滑行,并撞上故障车,且推着它共同滑行了一段距离l后停下.事故发生后,经测量,卡车刹车时与故障车距离为L,撞车后共同滑行的距离l=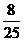 L.假定两车轮胎与雪地之间的动摩擦因数相同.已知卡车质量M为故障车质量m的4倍.
L.假定两车轮胎与雪地之间的动摩擦因数相同.已知卡车质量M为故障车质量m的4倍.
(1)设卡车与故障车相撞前的速度为v1,两车相撞后的速度变为v2,求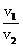 ;
;
(2)卡车司机至少在距故障车多远处采取同样的紧急刹车措施,事故才能免于发生.
答案 (1)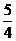 (2)
(2) 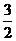 L
L
解析 (1)由碰撞过程动量守恒知
Mv1=(M+m)v2 TH①
则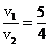
(2)设卡车刹车前速度为v0,轮胎与雪地之间的动摩擦因数为μ,两车相撞前卡车动能变化
 Mv02-
Mv02- Mv12=μMgL ②
Mv12=μMgL ②
碰撞后两车共同向前滑动到最后静止,动能变化
 (M+m)v22-0=μ(M+m)gl ③
(M+m)v22-0=μ(M+m)gl ③
由②式得v02-v12=2μgL
由③式得v22=2μgl
又因l=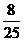 L,得v02=3μgL
L,得v02=3μgL
如果卡车滑到故障车前刚好停止,由
 Mv02-0=μMgL′ ④
Mv02-0=μMgL′ ④
故L′=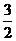 L
L
这意味着卡车司机在距故障车至少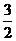 L处紧急刹车,事故就能够免于发生.
L处紧急刹车,事故就能够免于发生.
1. (05广东18) 如图所示,两个完全相同的质量为m的木板A、B置
(05广东18) 如图所示,两个完全相同的质量为m的木板A、B置
于水平地面上,它们的间距s=2.88 m.质量为2m、大小可忽略的物
块C置于A板的左端.C与A之间的动摩擦因数为μ1=0.22,A、B与水平地面之间的动摩擦因数为μ2=0.10,最大静摩擦力可认为等于滑动摩擦力.开始时,三个物体处于静止状态.现给C施加一个水平向右,大小为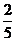 mg的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起.要使C最终不脱离木板,每块木板的长度至少应为多少?
mg的恒力F,假定木板A、B碰撞时间极短且碰撞后粘连在一起.要使C最终不脱离木板,每块木板的长度至少应为多少?
答案 0.3 m?
解析 设A、C之间的滑动摩擦力大小为f1,A与水平地面之间的滑动摩擦力大小为f2
∵μ1=0.22,μ2=0.10
∴F=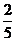 mg<f1=2μ1mg
mg<f1=2μ1mg
且F=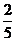 mg>f2=μ2(2m+m)g
mg>f2=μ2(2m+m)g
∴一开始A和C保持相对静止,在F的作用下向右加速运动,有
(F-f2)·s= (2m+m)v12
(2m+m)v12
A、B两木板的碰撞瞬间,内力的冲量远大于外力的冲量,A、B组成的系统动量守恒,由动量守恒定律得:
mv1=(m+m)v2
碰撞结束后三个物体达到共同速度的相互作用过程中,设木板向前移动的位移为x1,选三个物体构成的整体为研究对象,外力之和为零,则
2mv1+(m+m)v2=(2m+m+m)v3
设A、B系统与水平地面之间的滑动摩擦力大小为f3,对A、B系统,由动能定理
f1·s1-f3·s1= ·2mv32-
·2mv32- ·2mv22
·2mv22
f3=μ2(2m+m+m)g
对C物体,由动能定理
F·(2l+x1)-f1·(2l+x1)=  ·2mv32-
·2mv32- ·2mv12
·2mv12
由以上各式、再代入数据可得l=0.3 m
12.(2005江苏18)如图所示,三个质量均为m的弹性小球用两根长均为L的轻绳连成一条直线而静止在光滑水平面上,现给中间的小球B一个水平初速度v0,方向与绳垂直,小球相互碰撞时无机械能损失,轻绳不可伸长.求:
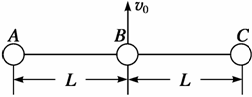 (1)当小球A、C第一次相碰时,小球B的速度;
(1)当小球A、C第一次相碰时,小球B的速度;
(2)当三个小球再次处在同一直线上时,小球B的速度;
(3)运动过程中小球A的最大动能EkA和此时两根绳的夹角θ;
(4)当三个小球处在同一直线上时,绳中的拉力F的大小.
答案 (1)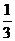 v0 (2)-
v0 (2)-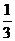 v0 (3)90° (4)m
v0 (3)90° (4)m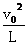
解析 (1)设小球A、C第一次相碰时,小球B的速度为vB,考虑到对称性及绳的不可伸长特性,小球A、C沿小球B初速度方向的速度也为vB.由动量守恒定律,得mv0=3mvB
由此解得vB=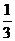 v0
v0
(2)当三个小球再次处在同一直线上时,则由动量守恒定律和机械能守恒定律,得
mv0=mvB+2mvA
 mv02=
mv02= mvB2+2×
mvB2+2× mvA2
mvA2
解得vB=-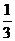 v0,vA=
v0,vA= v0(三球再次处于同一直线)
v0(三球再次处于同一直线)
vB=v0,vA=0(初始状态,舍去)
所以三个小球再次处在同一直线上时,小球B的速度为
vB=-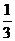 v0(负号表明与初速度方向相反)
v0(负号表明与初速度方向相反)
(3)当小球A的动能最大时,小球B的速度为零.设此时小球A、C的速度大小为u,两根绳间夹角为θ,则仍由动量守恒定律和机械能守恒定律,得:
mv0=2musin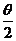
 mv02=2×
mv02=2× mu2
mu2
另外,EkA= mu2
mu2
由此解得,小球A的最大动能为:
EkA=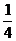 mv02
mv02
此时两根绳间夹角为θ=90°
(4)小球A、C均以半径L绕小球B做圆周运动,当三个小球处在同一直线上时,以小球B为参考系(小球B的加速度为零,为惯性参考系),小球A、C相对小球B的速度均为:
v=|vA-vB|=v0
所以,此时绳中拉力大小为:F=m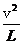 =m
=m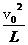
题组三
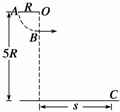
11.(05全国理综Ⅱ25)如图所示,一对杂技演员(都视为质点)乘秋千(秋千绳处于水
平位置)从A点由静止出发绕O点下摆,当摆到最低点B时,女演员在极短时间内将
男演员沿水平方向推出,然后自己刚好能回到高处A.求男演员落地点C与O点的水
平距离s.已知男演员质量m1和女演员质量m2之比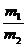 =2,秋千的质量不计,秋千的摆长为R,C点比O点低5R. 答案 8 R
=2,秋千的质量不计,秋千的摆长为R,C点比O点低5R. 答案 8 R
解析 设分离前男女演员在秋千最低点B的速度为v0,由机械能守恒定律得
(m1+m2)gR= (m1+m2)v02 ①
(m1+m2)v02 ①
设刚分离时男演员速度大小为v1,方向与v0相同;女演员速度大小为v2,方向与v0相反,由动量守恒得(m1+m2)v0=m1v1-m2v2 ②
分离后,男演员做平抛运动,设男演员从被推出到落在C点所需的时间为t,根据题给条件,由运动学规律
4R= gt2 ③
gt2 ③
s=v1t ④
分离后,女演员恰回到A点,由机械能守恒定律
m2gR= m2v22 ⑤
m2v22 ⑤
已知m1=2m2 ⑥
由以上各式得:s=8 R ⑦
10.(05天津理综24)如图所示,质量mA为4.0 kg的木板A放在水平面C上,
木板与水平面间的动摩擦因数μ为0.24,木板右端放着质量mB为1.0 kg的
小物块B(视为质点),它们均处于静止状态.木板突然受到水平向右的12 N·s的瞬时冲量I作用开始运动,当小物块滑离木板时,木板的动能EKA为8.0 J,小物块的动能EKB为0.50 J,重力加速度取10 m/s2,求:
(1)瞬时冲量作用结束时木板的速度v0;
(2)木板的长度L.
答案 (1)3.0 m/s (2)0.50 m?
解析(1)设水平向右为正方向,有
I=mAv0 ①
代入数据解得
v0=3.0 m/s ②
(2)设A对B、B对A、C对A的滑动摩擦力的大小分别为FAB、FBA和FCA,B在A上滑行的时间为t,B离开A时A和B的速度分别为vA和vB,有
-(FBA+FCA)t=mAvA-mAv0 ③
FABt=mBvB ④
其中FAB=FBA
FCA=μ(mA+mb)g ⑤
设A、B相对于C的位移大小分别为SA和SB,
有-(FBA+FCA)SA= mAvA2-
mAvA2- mAv02 ⑥
mAv02 ⑥
FABSB=EKB ⑦
动量与动能之间的关系为
mAvA=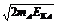 ⑧
⑧
mBvB= 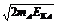 ⑨
⑨
木板A的长度
L=sA-sB ⑩
代入数据解得
 L=0.50 m
L=0.50 m
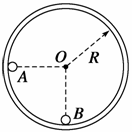
9.(2006重庆理综25)如图所示,半径为R的光滑圆形轨道固定在竖直面内.小球
A、B质量分别为m、βm(β为待定系数).A球从左边与圆心等高处由静止开始沿轨
道下滑,与静止于轨道最低点的B球相撞,碰撞后A、B球能达到的最大高度均为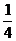 R,
R,
碰撞中无机械能损失.重力加速度为g.试求:
(1)待定系数β;
(2)第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力;
(3)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度.
答案 (1)β=3 (2)A:v1=-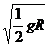 ,方向向左;B:v2=
,方向向左;B:v2=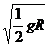 ,方向向右;4.5 mg,方向竖直向下
,方向向右;4.5 mg,方向竖直向下
(3)A:V1=-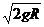 , B:V2=0.当n为奇数时,小球A、B第n次碰撞结束时的速度分别与其第一次碰撞刚结束时相同.
, B:V2=0.当n为奇数时,小球A、B第n次碰撞结束时的速度分别与其第一次碰撞刚结束时相同.
当n为偶数时,小球A、B在第n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同.
解析 (1)由mgR=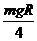 +
+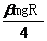 得β=3
得β=3
(2)设A、B碰撞后的速度分别为v1、v2,则
 mv12=
mv12=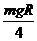
 βmv22=
βmv22=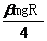
设向右为正、向左为负,得
v1=-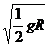 ,方向向左
,方向向左
v2=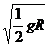 ,方向向右
,方向向右
设轨道对B球的支持力为N,B球对轨道的压力为N′,方向竖直向上为正、向下为负,
则N-βmg=βm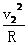
N′=-N=-4.5 mg,方向竖直向下
(3)设A、B球第二次碰撞刚结束时的速度分别为V1、V2,则
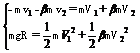
解得V1=- 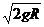 ,V2=0
,V2=0
(另一组解:V1=-v1,V2=-v2不合题意,舍去)
由此可得:
 当n为奇数时,小球A、B在第n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同;当n为偶数时,小球A、B在第n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同.
当n为奇数时,小球A、B在第n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同;当n为偶数时,小球A、B在第n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同.
8.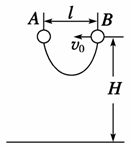 (2006江苏17)如图所示,质量均为m的A、B两个弹性小球,用长为2l的不可
(2006江苏17)如图所示,质量均为m的A、B两个弹性小球,用长为2l的不可
伸长的轻绳连接.现把A、B 两球置于距地面高H处(H足够大),间距为l,当A球
自由下落的同时,将B球以速度v0指向A球水平抛出,求:
(1)两球从开始运动到相碰,A球下落的高度;
(2)A、B两球碰撞(碰撞时无机械能损失)后,各自速度的水平分量;
(3)轻绳拉直过程中,B球受到绳子拉力的冲量大小.
答案 (1) 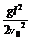 (2)v0 0 (3)
(2)v0 0 (3) 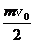
解析 (1)设A球下落的高度为h
l=v0t ①
h= gt2 ②
gt2 ②
联立①②得h=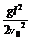 ③
③
(2)由水平方向动量守恒得
mv0=mvAx′+mvBx′ ④
由机械能守恒得
 m(v02+vBy2)+
m(v02+vBy2)+  mvAy2=
mvAy2= m(vAx′2+vAy′2)+
m(vAx′2+vAy′2)+  m(vBx′2+vBy′2) ⑤
m(vBx′2+vBy′2) ⑤
式中vAy′=vAyvBy′=vBy
联立④⑤得vAx′=v0,vBx′=0
(3)由水平方向动量守恒得
mv0=2mvBx″
 则I=mv0-mvBx″=
则I=mv0-mvBx″=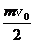
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com